Высота прямоугольного треугольника – это отрезок, опущенный из вершины прямого угла на противоположную катету или гипотенузу. Нахождение высоты треугольника важно во многих сферах, включая геометрию, строительство и инженерное дело. В этой статье рассмотрим, как найти высоту прямоугольного треугольника, зная значение его гипотенузы.

Для нахождения высоты прямоугольного треугольника по гипотенузе необходимо использовать теорему Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов. Это позволяет нам определить длину другого катета, а затем найти площадь треугольника и, соответственно, его высоту.

Предположим, что известна длина гипотенузы треугольника (символизируется буквой c). Чтобы найти высоту (h) треугольника, нужно сначала найти длину одного из катетов. Для этого можно воспользоваться формулой Пифагора: с² - a² = b², где a и b – катеты треугольника. После нахождения длины одного из катетов, площадь треугольника находится по формуле (a * b) / 2. Зная площадь треугольника и длину одного из катетов, можно найти высоту при помощи следующей формулы: h = (2 * площадь) / основание.

Определение высоты прямоугольного треугольника

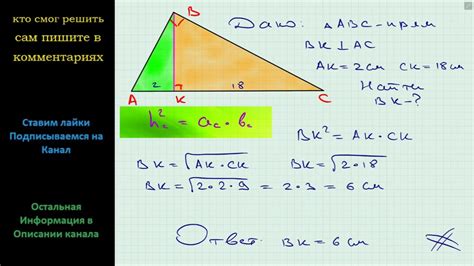
Чтобы найти высоту прямоугольного треугольника, необходимо использовать теорему Пифагора, которая гласит, что сумма квадратов катетов равна квадрату гипотенузы. Для решения этой задачи мы можем использовать следующую формулу:

Высота = (катет₁ * катет₂) / гипотенуза

Применяя данную формулу, мы можем найти значение высоты прямоугольного треугольника даже если известны только значения длины его катетов или гипотенузы.

Если катеты уже известны, можно найти площадь прямоугольного треугольника, умножив длину катета, значение высоты и разделив результат на 2, поскольку площадь треугольника равна половине произведения одной из его сторон на высоту, опущенную на эту сторону.

Вычисление высоты треугольника через катеты:

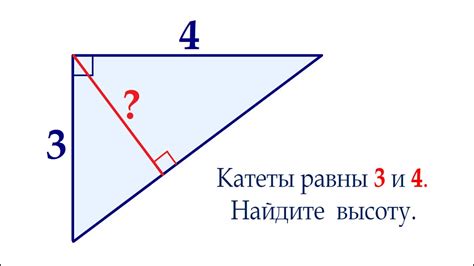
Чтобы найти высоту прямоугольного треугольника по длине его катетов, можно воспользоваться формулой:

Высота = (первый катет * второй катет) / гипотенуза

Где:

• Первый катет - длина одного из катетов треугольника;
• Второй катет - длина другого катета треугольника;
• Гипотенуза - длина гипотенузы треугольника.

Чтобы вычислить высоту, необходимо знать длины обоих катетов и гипотенузу.

Пример вычисления: допустим, первый катет равен 6, второй катет равен 8, а гипотенуза равна 10.

Тогда высота треугольника будет равна:

((6 * 8) / 10) = 4.8

Таким образом, высота прямоугольного треугольника, заданного катетами 6 и 8, при гипотенузе равной 10, составляет 4,8 единицы длины.

Как определить высоту треугольника, зная его площадь:

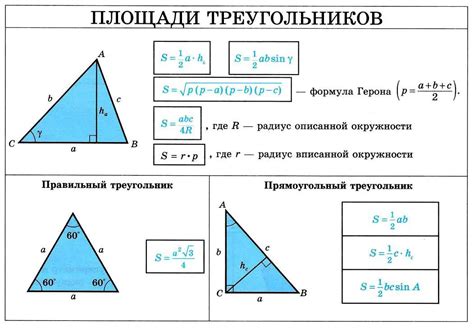
Для определения высоты треугольника, зная его площадь, нужно знать одну из его сторон и площадь. Если известна основание треугольника (одна из его сторон), можно использовать следующую формулу:

где:

• h - высота треугольника;
• S - площадь треугольника;
• a - длина основания треугольника.

Пример:

Предположим, что площадь треугольника равна 24 квадратных см, а длина основания равна 8 см. Чтобы найти высоту треугольника, используем формулу:

h = (2 * 24) / 8 = 6 см

Таким образом, высота треугольника равна 6 см. Это позволяет определить длину перпендикулярной стороны, относительно которой измеряется высота.

Методы вычисления высоты треугольника:

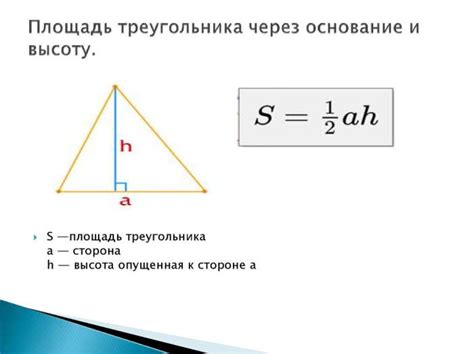
Существует несколько способов вычисления высоты прямоугольного треугольника по его гипотенузе:

1. Формула площади:

Высота треугольника может быть найдена с использованием формулы площади, которая основана на прямоугольном треугольнике.

Формула для вычисления высоты треугольника по гипотенузе и одной из его сторон:

h = (2 * S) / c

где h - высота треугольника, S - площадь треугольника, c - длина гипотенузы.

2. Теорема Пифагора:

Если треугольник прямоугольный, то существует связь между длинами его сторон: гипотенузы и катетов. Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.

Для вычисления высоты треугольника можно использовать теорему Пифагора следующим образом:

h = (a * b) / c

где h - высота треугольника, a и b - длины катетов, c - длина гипотенузы.

3. Тригонометрические функции:

Треугольник прямоугольный, поэтому можно использовать тригонометрические функции для вычисления высоты треугольника.

Формулы для вычисления высоты треугольника:

h = a * sin(B)

h = b * sin(A)

где h - высота треугольника, a и b - длины катетов, A и B - соответствующие углы треугольника.

Выбранный метод вычисления высоты треугольника зависит от задачи и доступных данных. Все эти методы основываются на свойствах прямоугольного треугольника и могут быть применены для определения высоты треугольника по его гипотенузе.

Примеры задач по определению высоты треугольника:

• Задача 1:

В прямоугольном треугольнике гипотенуза равна 10 см, а катет равен 6 см. Найдите высоту, опущенную на гипотенузу.

• Задача 2:

Дан прямоугольный треугольник с гипотенузой длиной 15 м и высотой, опущенной на эту гипотенузу, равной 9 м. Найдите второй катет треугольника.

• Задача 3:

В прямоугольном треугольнике один катет равен 12 см, а второй катет равен 5 см. Найдите длину высоты, опущенной из прямого угла треугольника.

• Задача 4:

Прямоугольный треугольник имеет гипотенузу равную 17 см. Известно, что высота, опущенная на гипотенузу, равна 8 см. Найдите длину одного из катетов треугольника.

Значение высоты треугольника в геометрии:

Зная значение гипотенузы прямоугольного треугольника (самой длинной стороны), можно вычислить значение его высоты. Для этого нужно воспользоваться формулой: высота треугольника равняется половине произведения катета, проведенного к основанию треугольника, и его гипотенузы, деленной на длину гипотенузы.

Таким образом, если известна длина гипотенузы треугольника, можно легко вычислить значение его высоты, что может быть полезно при нахождении площади треугольника или решении задач связанных с прямоугольными треугольниками.