Высота равнобедренной трапеции - один из основных параметров, необходимых для решения множества геометрических задач. Трапеция - это четырехугольник, у которого две стороны параллельны. Вид равнобедренной трапеции характеризуется тем, что основания равны, а боковые стороны - равны. Примечательно то, что для нахождения высоты такой трапеции необязательно знать ее площадь.
Для нахождения высоты равнобедренной трапеции без использования площади можно воспользоваться теоремой Пифагора или теоремой синусов. Первый способ основан на знании длин основания и боковых сторон, а второй способ требует знания длин основания и одного угла трапеции.
Используя теорему Пифагора, можно найти высоту равнобедренной трапеции по формуле h = sqrt(b^2 - L^2), где h - высота, b - длина основания, L - длина боковой стороны. Если известны углы трапеции, можно воспользоваться теоремой синусов для нахождения высоты. Формула будет выглядеть следующим образом: h = (b * sin(A)) / sin(B), где h - высота, b - длина основания, A - угол при основании, B - угол между основанием и боковой стороной.
Постановка задачи

Для решения данной задачи потребуется знание длин оснований трапеции и ее боковой стороны. Высота равнобедренной трапеции - это расстояние между ее параллельными сторонами. Она является важным параметром для вычисления площади трапеции и других характеристик этой фигуры.
Рассмотрим пример для наглядности. Пусть длины оснований трапеции равны 6 и 10, а длина боковой стороны равна 4. Необходимо найти высоту этой трапеции. Для решения данной задачи можно использовать теорему Пифагора или другие методы математического анализа.
Решая данную задачу, необходимо учесть, что высота равнобедренной трапеции может быть найдена без использования площади фигуры. Данная информация может быть полезна для различных задач геометрического исследования, проектирования, архитектуры и других областей знаний.
Таким образом, нахождение высоты равнобедренной трапеции без использования площади позволяет упростить и ускорить решение задач, связанных с этой геометрической фигурой.
Что такое равнобедренная трапеция
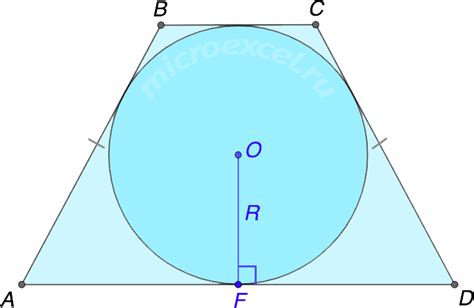
Равнобедренная трапеция: | Высота, опущенная на основание: |
Высота равнобедренной трапеции играет важную роль при решении различных задач. Чтобы найти высоту, необходимо знать длину основания и угол при вершине, а также другие известные параметры трапеции. Высота равнобедренной трапеции может быть найдена с использованием различных методов, например, используя теорему Пифагора, теорему косинусов или с помощью подобия треугольников.
Формула для вычисления площади
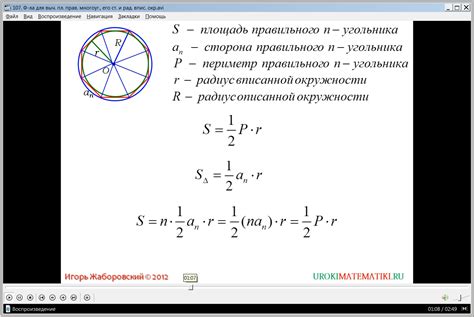
Площадь равнобедренной трапеции можно вычислить, зная ее боковую сторону (основание) и высоту. Формула для вычисления площади равнобедренной трапеции имеет следующий вид:
S = ((a + b) * h) / 2
Где:
- a - длина одной из оснований трапеции
- b - длина другого основания трапеции
- h - высота трапеции, проведенная на основания
Для вычисления площади равнобедренной трапеции необходимо сложить длины оснований, умножить полученную сумму на высоту и разделить на 2.
Например, если одно основание трапеции равно 5 см, а другое 10 см, а высота равна 8 см, то площадь трапеции будет равна:
S = ((5 + 10) * 8) / 2 = 60 см²
Таким образом, площадь равнобедренной трапеции с указанными размерами составляет 60 квадратных сантиметров.
Применение формулы площади

Высота равнобедренной трапеции может быть найдена с использованием формулы площади этой трапеции. Для этого нужно знать длины оснований и длину боковой стороны трапеции.
Формула площади равнобедренной трапеции выглядит следующим образом:
S = (a + b) * h / 2
где S - площадь трапеции, a и b - длины оснований, h - высота трапеции.
Если известны длины оснований и площадь трапеции, можно использовать эту формулу для нахождения высоты:
h = 2 * S / (a + b)
Таким образом, зная значения оснований и площади трапеции, можно рассчитать её высоту с помощью формулы площади.
Применение этой формулы позволяет установить значение высоты равнобедренной трапеции даже без её измерения напрямую, что может быть полезным в решении геометрических задач и нахождении неизвестных параметров трапеции.
Как найти стороны равнобедренной трапеции
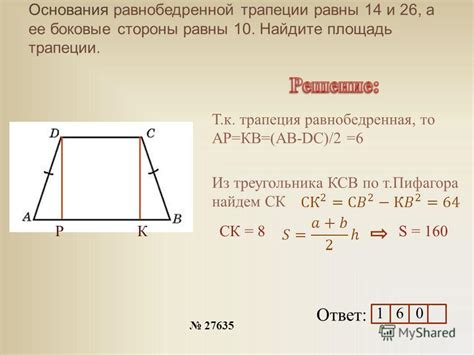
Для этого используется теорема Пифагора, которая утверждает, что в прямоугольном треугольнике с гипотенузой в качестве основания и катетами в качестве сторон, сумма квадратов катетов равна квадрату гипотенузы: a^2 + b^2 = c^2.
Предположим, что a и b – это основания равнобедренной трапеции, а c – это одна из боковых сторон (равные стороны) этой трапеции. Тогда, зная высоту h, можно составить уравнение с использованием теоремы Пифагора:
a^2 + h^2 = c^2
b^2 + h^2 = c^2
Таким образом, выразив основания через высоту и сторону, можно найти значения оснований равнобедренной трапеции по формулам:
a = √(c^2 - h^2)
b = √(c^2 - h^2)
Где a и b – это длины оснований равнобедренной трапеции, c – это длина боковой стороны (равной стороны) трапеции, а h – это длина высоты трапеции.
Высота равнобедренной трапеции без использования площади

Для нахождения высоты равнобедренной трапеции без использования площади можно воспользоваться теоремой Пифагора. Если основание трапеции делится на две равные части, а прямая, проведенная из вершины прямоугольного треугольника, перпендикулярна к основанию, то длина этой прямой будет равна высоте трапеции.
Для определения высоты равнобедренной трапеции можно использовать следующую формулу:
h = √(a^2 - c^2/4)
Где:
h - высота трапеции,
a - длина каждого основания трапеции,
c - длина боковой стороны трапеции (диагональ).
Таким образом, зная длины оснований и боковой стороны равнобедренной трапеции, можно легко найти высоту трапеции с помощью этой формулы.
