Косинус треугольника – это одно из фундаментальных понятий геометрии, которое позволяет нам определить углы треугольника с помощью его сторон. Расчет косинуса треугольника имеет широкое применение в различных областях, от строительства до тригонометрии.
Существует несколько способов вычисления косинуса треугольника, одним из которых является теорема косинусов. Этот метод основан на соотношении между сторонами треугольника и косинусами его углов.
Для расчета косинуса треугольника по его сторонам можно воспользоваться следующей формулой:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Где A - угол в радианах, а a, b и c - длины сторон треугольника.
Используя данную формулу, вы можете с легкостью определить косинус любого угла треугольника, зная длины его сторон. Это позволит вам решать различные геометрические задачи и получать точные значения углов треугольников.
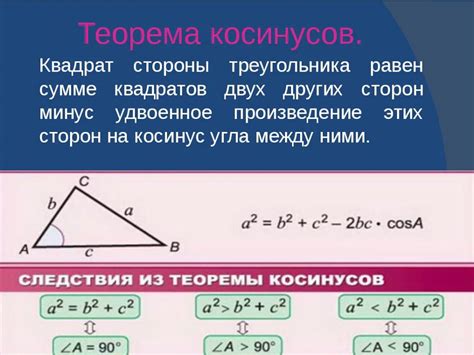
Сущность и принципы косинусной теоремы

Суть косинусной теоремы заключается в следующем: в треугольнике со сторонами a, b и c и найденным углом α, мы можем рассчитать отсутствующие стороны или углы, используя косинусы этих углов и формулу
cosα = (b² + c² - a²) / 2bc
где а, b и c - стороны треугольника.
Для рассчета косинусов других углов треугольника мы можем использовать аналогичные формулы, в которых неизвестными будут другие стороны.
Косинусная теорема широко применяется в различных областях, включая физику, инженерию и геодезию. Она позволяет определить форму треугольника и его свойства, а также проводить вычисления и измерения.
При использовании косинусной теоремы необходимо учитывать её ограничения: она применима только к треугольникам, а не к другим многоугольникам, и необходимо обратить внимание на выбор правильных углов и сторон для рассчета.
Важно знать и уметь применять косинусную теорему для решения геометрических и физических задач и расчетов, а также понимать её основные принципы и связь между сторонами и углами треугольника.
Определение треугольника и его углов

Для полного определения треугольника необходимо знать длины всех его сторон. Также, важно знать, какие углы образуются между этими сторонами.
Углы треугольника могут быть остроугольными, прямоугольными или тупоугольными.
Остроугольный треугольник имеет три острых угла, каждый из которых меньше 90 градусов.
Прямоугольный треугольник имеет один прямой угол, равный 90 градусов. Другие два угла являются острыми.
Тупоугольный треугольник имеет один тупой угол, больше 90 градусов. Остальные два угла являются острыми.
Углы треугольника также могут быть равными или неравными.
Равные углы называются равными и обозначаются одинаковыми буквами. Например, углы А и В равны, если А=В.
Неравные углы обозначаются разными буквами. Например, углы А и В неравны, если А не равно В.
Определение треугольника и его углов очень важно для вычислений, связанных со сторонами и углами треугольника, таких как расчет косинуса треугольника по сторонам.
Описание формулы для расчета косинуса треугольника
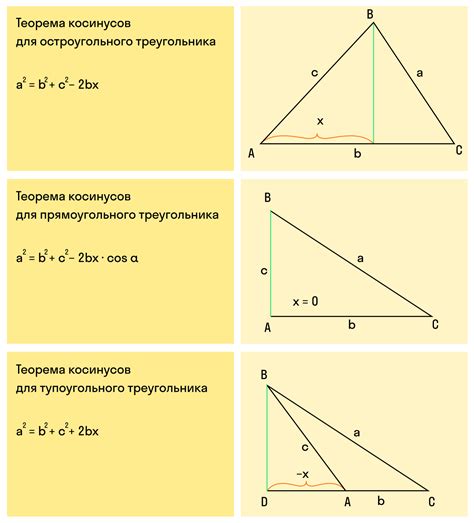
Для расчета косинуса треугольника по сторонам необходимо использовать формулу, которая основывается на теореме косинусов. Эта формула позволяет найти косинус угла, противолежащего наибольшей стороне треугольника, зная длины всех трех сторон.
Формула для расчета косинуса треугольника выглядит следующим образом:
| cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) |
| cos(B) = (a^2 + c^2 - b^2) / (2 * a * c) |
| cos(C) = (a^2 + b^2 - c^2) / (2 * a * b) |
Где A, B и C - углы треугольника, a, b и c - длины сторон, противолежащие этим углам.
Используя эти формулы, можно вычислить косинус каждого угла треугольника по его сторонам. Зная значения косинусов углов, можно рассчитать различные характеристики треугольника, такие как площадь, периметр и т.д.
Примеры применения косинусной теоремы

- Вычисление углов треугольника: с помощью косинусной теоремы можно найти все углы треугольника, если известны длины его сторон. Достаточно применить формулу cos(A) = (b^2 + c^2 - a^2) / (2 * b * c), где A - угол против стороны a.
- Нахождение длины стороны треугольника: если известны все три угла треугольника и длины двух его сторон, можно вычислить длину третьей стороны, используя косинусную теорему. Формула для этого выглядит следующим образом: a^2 = b^2 + c^2 - 2bc * cos(A), где a - третья сторона, b и c - известные стороны, A - угол против стороны a.
- Расчет площади треугольника: зная длины всех сторон треугольника, можно вычислить его площадь с помощью косинусной теоремы. Формула для этого выглядит следующим образом: S = (1/2) * a * b * sin(C), где a и b - стороны треугольника, C - угол между ними.
- Определение вида треугольника: с помощью косинусной теоремы можно определить, является ли треугольник остроугольным, тупоугольным или прямоугольным. Если a^2 + b^2 - c^2 = 0, то треугольник прямоугольный. Если a^2 + b^2 - c^2 0, то треугольник остроугольный.
- Решение геодезических задач: косинусная теорема используется в геодезии для определения расстояния между двумя точками на Земле, если известны их координаты. Это позволяет найти длину дуги между двумя точками на сферической поверхности.
Это лишь некоторые примеры применения косинусной теоремы. Она является мощным инструментом в геометрии и находит широкое применение в различных областях науки и техники.
Практическое применение косинусной теоремы в сфере постройки и геодезии
В геодезии косинусная теорема применяется для определения углов треугольника на земной поверхности. Зная длины трех сторон треугольника, можно вычислить косинус каждого из углов и, соответственно, сам угол. Это позволяет определить географические координаты точек на местности, проводить измерения и построение картографических сеток.
Также косинусная теорема применяется в сфере постройки, особенно при решении задач, связанных с треугольными профилями. Расчеты по этой теореме позволяют определить высоты и углы в треугольных участках зданий, что является важным доменом в процессе строительства. Например, при проектировании крыши здания, зная значения двух сторон и угла между ними, можно расчитать длину третьей стороны и определить форму крыши.
| Известные данные | Расчетные значения |
|---|---|
| Сторона A: 10 м | Угол A: 60° |
| Сторона B: 5 м | Угол B: 30° |
| Сторона C: 8.66 м |
Таким образом, косинусная теорема является мощным инструментом в геометрических расчетах и находит широкое применение в сфере постройки и геодезии. Благодаря этой теореме можно определять углы и стороны треугольника, что позволяет производить точные измерения и строить объекты с высокой степенью точности.
Сравнение косинусной теоремы с другими методами вычисления треугольников

Один из наиболее популярных методов вычисления треугольников – это теорема Пифагора, которая применяется для прямоугольных треугольников. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов. Однако этот метод применим только к прямоугольным треугольникам и не может быть использован в других случаях.
Косинусная теорема, с другой стороны, может быть использована для вычисления всех видов треугольников, включая неравносторонние треугольники. Косинусная теорема устанавливает связь между длинами сторон треугольника и косинусами углов. С помощью этой теоремы можно вычислить любой угол треугольника, если известны длины всех его сторон.
Еще одним методом вычисления треугольников является использование теоремы синусов. Эта теорема устанавливает соотношение между длинами сторон треугольника и синусами углов. Теорема синусов также применима ко всем видам треугольников, но имеет некоторые ограничения. Например, она требует знания двух сторон треугольника и угла между ними или знания двух углов и длины между ними стороны. В то время как косинусная теорема позволяет вычислять углы треугольника, используя только длины его сторон.
В итоге, косинусная теорема предоставляет простой и универсальный способ вычисления треугольников. Она может быть использована для решения широкого спектра задач, начиная от нахождения углов в треугольнике до определения длин сторон. Преимущества косинусной теоремы включают ее широкую применимость и высокую точность результатов.
| Метод | Применимость | Ограничения |
|---|---|---|
| Косинусная теорема | Для всех видов треугольников, включая неравносторонние | Требуется знание длин всех сторон треугольника |
| Теорема Пифагора | Для прямоугольных треугольников | Не применима к другим видам треугольников |
| Теорема синусов | Для всех видов треугольников | Требуется знание двух сторон и угла или двух углов и стороны треугольника |
Преимущества использования косинусной теоремы

Одним из основных преимуществ использования косинусной теоремы является то, что она позволяет вычислять косинус углов треугольника без необходимости знания всех трех углов. Достаточно знать только значения сторон треугольника, чтобы определить косинус каждого угла.
Кроме того, косинусная теорема позволяет решать задачи обратного характера. Например, если известны значения угла и двух сторон треугольника, можно вычислить значение третьей стороны. Это особенно полезно при решении практических задач, связанных с измерением расстояний или нахождением неизвестных размеров.
Косинусная теорема также позволяет определить тип треугольника - остроугольный, тупоугольный или прямоугольный - исходя из значений сторон и углов треугольника. Такая информация может быть полезной для анализа геометрических объектов и решения задач в физике и инженерии.
При использовании косинусной теоремы также можно выявить зависимости между углами и сторонами треугольника. Например, если одна сторона увеличивается или уменьшается, то углы треугольника также изменяются. Это помогает в анализе треугольников и построении математических моделей для предсказания их свойств и поведения.
Использование косинусной теоремы позволяет сократить количество неизвестных переменных и упростить расчеты, поскольку она позволяет связать значения сторон и углов треугольника с помощью единой формулы. Это облегчает решение задач и делает процесс более систематичным и логичным.
В целом, косинусная теорема является мощным инструментом для решения задач, связанных с треугольниками, и обладает множеством преимуществ, делающих ее полезной в различных областях науки и техники.