Синус и косинус - две взаимосвязанные тригонометрические функции, которые широко применяются во многих науках и инженерных расчетах. Синус определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике, а косинус - как отношение прилежащего катета к гипотенузе. Обычно эти функции вычисляются с помощью таблиц или специальных программ, однако существует простой и быстрый способ получить значение синуса из косинуса и наоборот - с использованием калькулятора.

В случае, если у вас есть известное значение косинуса или синуса, и вам нужно найти значение другой функции, можно воспользоваться тригонометрическими тождествами. Одно из них гласит, что синус и косинус комплиментарного угла (дополнительного к заданному) равны друг другу с противоположными знаками. То есть, если у вас есть значение косинуса, можно легко найти значение синуса, поменяв знак. Например, если cos(α) = 0,643, то sin(α) = -0,643.

Калькуляторы старых моделей могут не иметь специальной кнопки для вычисления синуса или косинуса, но вы можете легко получить значение нужной функции, зная значение другой. Такой прием особенно полезен, когда необходимо быстро найти значение функции без использования сложных расчетов или таблиц. Это позволяет сэкономить время и избежать возможных ошибок в вычислениях.

Формула и алгоритм

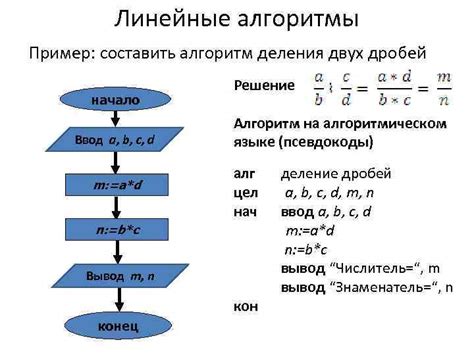
Для вычисления синуса из косинуса существует специальная формула, которая основана на соотношении между тригонометрическими функциями.

Согласно этой формуле, синус угла равен квадратному корню из единицы минус квадрат косинуса угла.

Таким образом, синус угла можно выразить следующей формулой:

sin(x) = sqrt(1 - cos(x)^2)

Для определения значения синуса угла с помощью данной формулы требуется сначала вычислить значение косинуса угла. Затем выполняется возведение в квадрат полученного значения и извлечение корня из разности со значением единицы.

Данный алгоритм позволяет найти синус угла на основе известного значения косинуса с минимальными вычислительными затратами.

Преимущества использования

Использование калькулятора для нахождения синуса из косинуса обладает рядом преимуществ, которые делают этот инструмент неотъемлемой частью работы с тригонометрическими функциями.

• Быстрота и удобство: Калькулятор предоставляет возможность мгновенно получить результат вычисления без необходимости выполнять ручные расчеты или использовать сложные формулы.
• Точность: При помощи калькулятора можно получить точный ответ с высокой степенью точности. Это особенно важно при работе с научными и инженерными расчетами, где даже небольшие неточности могут существенно повлиять на результаты и анализ.
• Экономия времени: Использование калькулятора позволяет существенно сэкономить время, освободив пользователя от необходимости проводить длительные вычисления вручную. Это особенно полезно при работе с большими объемами данных или при выполнении повторяющихся операций.
• Универсальность: Калькулятор для нахождения синуса из косинуса может быть использован в различных сферах, включая математику, физику, инженерное дело, компьютерную графику и другие области, где требуется работа с тригонометрическими функциями.

Все эти преимущества в сочетании делают калькулятор нахождения синуса из косинуса неотъемлемым инструментом для быстрого и точного выполнения вычислений с использованием тригонометрических функций.

Примеры применения в практике

Калькулятор, который позволяет вычислить синус из косинуса, имеет множество применений в различных отраслях и задачах. Вот несколько примеров, где его использование может быть полезным:

1. Геодезия: При работе с геодезическими измерениями, вычисление значений синуса или косинуса может пригодиться для определения угла наклона поверхности земли или высоты объекта. Например, при рассчете высоты горы или наклона склона.

2. Физика: В физических расчетах с использованием гармонических функций, синусы и косинусы применяются для моделирования движения, колебаний и волн. Например, при изучении движения материальной точки по окружности или колебаний маятника.

3. Криптография: В криптографических алгоритмах, таких как шифр RSA, вычисление косинуса и синуса может быть использовано для генерации криптографических ключей и обеспечения безопасности передаваемой информации.

4. Активности на олимпиадах: Задачи, связанные с вычислением синуса из косинуса, могут появиться на математических олимпиадах или соревнованиях по физике, где необходимо проявить знания и умения в области тригонометрии.

5. Программирование: В разработке программного обеспечения, использование функций синуса и косинуса может быть полезно для решения различных задач и вычислений. Например, при построении графиков, анимаций или реализации математических моделей.

Калькулятор, позволяющий вычислить синус из косинуса, может быть полезным инструментом во многих областях науки, инженерии и математики. Его использование может ускорить и упростить решение задач и расчетов, где требуется точное значение синуса по известному косинусу.

• Калькулятор, позволяющий находить синус по значению косинуса, является полезным инструментом для математических расчетов.
• Такой калькулятор является простым и быстрым в использовании, что позволяет сократить время вычислений в задачах, связанных с тригонометрией.
• Синус и косинус являются основными элементами тригонометрии и широко применяются в научных и инженерных расчетах.
• Использование калькулятора позволяет избежать ошибок при вычислении синуса по значению косинуса и обеспечивает точность результатов.
• Калькулятор может быть использован в различных областях, включая физику, геометрию, астрономию и другие науки.
• Главным преимуществом данного калькулятора является его удобство и доступность для использования, как для профессионалов, так и для студентов.