Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. Эта фигура имеет много интересных свойств и особенностей. Одним из ключевых параметров параллелограмма является длина его диагоналей. В этой статье мы рассмотрим, как найти диагональ параллелограмма, зная его стороны и угол.
Дано: стороны параллелограмма - a и b, угол между этими сторонами - угол α.
Необходимо: найти длину диагонали параллелограмма.
Для решения этой задачи мы воспользуемся теоремой косинусов, которая связывает длины сторон треугольника с углами. Также нам понадобится знание обратной функции косинуса, называемой арккосинусом.
Способы вычисления диагонали параллелограмма
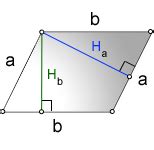
1. При наличии известных сторон и угла параллелограмма можно воспользоваться теоремой косинусов. Для этого необходимо знать длины двух сторон параллелограмма и величину угла между ними. По формуле косинусов можно вычислить длину диагонали, например, следующим образом:
| Формула косинусов: | |
|---|---|
| cos(α) = (a² + b² - c²) / (2 * a * b) | где α - угол между сторонами a и b, c - длина диагонали |
| c = √(a² + b² - 2 * a * b * cos(α)) | |
2. Если известны длины двух сторон и площадь параллелограмма, то можно воспользоваться формулой для вычисления высоты параллелограмма. Затем, используя теорему Пифагора, вычислить длину диагонали. Формула для вычисления высоты параллелограмма выглядит следующим образом:
| Формула для вычисления высоты параллелограмма: | |
|---|---|
| h = 2 * S / a | где h - высота параллелограмма, S - площадь, a - длина одной из сторон |
Получив значение высоты, можно применить теорему Пифагора:
| Теорема Пифагора: | |
|---|---|
| c² = a² + h² | где c - диагональ, a - одна из сторон, h - высота |
3. При известных сторонах и радиусе вписанной окружности параллелограмма можно воспользоваться формулой для вычисления полупериметра и длины диагонали. Формула для вычисления полупериметра параллелограмма выглядит следующим образом:
| Формула для вычисления полупериметра параллелограмма: | |
|---|---|
| p = a + b | где p - полупериметр, a и b - длины двух сторон |
С помощью полупериметра можно вычислить радиус вписанной окружности параллелограмма через следующую формулу:
| Формула для вычисления радиуса вписанной окружности: | |
|---|---|
| r = S / p | где r - радиус, S - площадь, p - полупериметр |
И наконец, зная радиус вписанной окружности и полупериметр, можно вычислить длину диагонали с помощью следующей формулы:
| Формула для вычисления диагонали параллелограмма: | |
|---|---|
| d = 2 * r * sin(π / 2) | где d - длина диагонали, r - радиус |
Описанные выше способы позволяют вычислить длину диагонали параллелограмма при различных известных значениях: сторон, углов, площади, радиуса вписанной окружности и полупериметра. Знание этих способов позволяет удобно и точно вычислить длину диагонали параллелограмма в различных ситуациях.
Метод 1: Формула синуса

Для вычисления диагонали параллелограмма по сторонам и углу можно использовать формулу синуса. Позволяет найти третью сторону параллелограмма, если известны две стороны и угол между ними.
Формула синуса:
d = 2 * a * sin(α)
где d - диагональ параллелограмма, a - длина одной из сторон, α - угол между этой стороной и диагональю.
Применение формулы синуса позволяет найти диагональ параллелограмма, если известны длины двух сторон и угол между ними. Этот метод особенно полезен, когда необходимо найти диагональ, но нет информации о других углах или сторонах параллелограмма.
Метод 2: Формула косинуса

Второй метод для нахождения диагонали параллелограмма по сторонам и углу использует формулу косинуса.
Пусть у нас есть параллелограмм, стороны которого обозначены как a и b, а угол между ними - как α.
Диагональ параллелограмма может быть найдена следующим образом:
d = √(a² + b² - 2ab⋅cosα)
Где:
- d - длина диагонали;
- a и b - длины сторон параллелограмма;
- α - угол между сторонами параллелограмма.
Данная формула основана на свойстве косинуса для треугольника.
Теперь, подставив в формулу известные значения, можно вычислить диагональ параллелограмма.
Пример решения:
Пусть сторона a равна 4, сторона b равна 6, а угол α равен 45 градусов.
Используя формулу косинуса и подставив значения:
d = √(4² + 6² - 2⋅4⋅6⋅cos45)
d = √(16 + 36 - 48⋅0,707) = √(52 - 33,9) = √18,1 ≈ 4,26
Таким образом, диагональ параллелограмма при данных значениях составляет около 4,26 единиц.