Вычисление синусов, косинусов и тангенсов углов является важной задачей в математике и науках, связанных с физикой и инженерией. Обычно для этой цели используются сложные математические формулы, которые могут быть сложными для понимания и реализации. Однако существует простой метод, позволяющий вычислить значения синуса, косинуса и тангенса углов без необходимости в использовании сложных формул.
Этот метод основан на разложении угла на простые шаги и использовании базовых соотношений между синусом, косинусом и тангенсом углов. Вместо использования тригонометрических функций и их сложных формул, мы можем использовать геометрические схемы и простые математические операции для вычисления значений этих функций.
Преимущество этого метода заключается в его простоте и понятности. Он не требует глубоких знаний в математике и может быть использован даже людьми без специального образования. Кроме того, данный метод позволяет получить точные значения синуса, косинуса и тангенса углов с высокой точностью, что является важным для многих практических ситуаций.
Простой метод вычисления синусов, косинусов и тангенсов углов
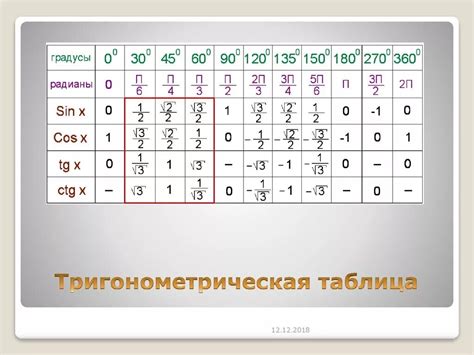
Один из таких простых методов основан на использовании математических таблиц и геометрических соображений. Для вычисления синуса, косинуса и тангенса угла нужно всего лишь знать его значение в градусах и использовать таблицы соответствующих тригонометрических функций.
Для примера, рассмотрим вычисление синуса угла 30°. Задача сводится к нахождению значения синуса для этого угла. В таблице синусов найдем строку с числом 30 и посмотрим значение в соответствующей колонке. Допустим, это значение равно 0.5. Тогда синус 30° равен 0.5.
Аналогичным образом можно вычислить косинус и тангенс угла, используя таблицы соответствующих функций. При этом нужно обратить внимание на аналогичную таблицу для косинусов и на таблицу для тангенсов.
Такой простой метод вычисления тригонометрических функций особенно удобен в ситуациях, когда нет возможности использовать сложные формулы или когда требуется быстро получить приближенное значение. Однако, стоит помнить, что этот метод не гарантирует абсолютной точности и может давать только приближенные значения.
Понятие синуса, косинуса и тангенса
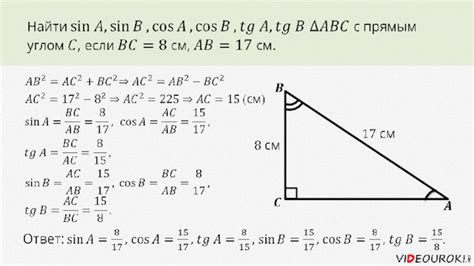
Синус (sin) угла в прямоугольном треугольнике определяется отношением длины противолежащего катета к гипотенузе. Выражается формулой: sin(угол) = противолежащий катет / гипотенуза.
Косинус (cos) угла в прямоугольном треугольнике определяется отношением длины прилежащего катета к гипотенузе. Выражается формулой: cos(угол) = прилежащий катет / гипотенуза.
Тангенс (tg) угла в прямоугольном треугольнике определяется отношением длины противолежащего катета к прилежащему катету. Выражается формулой: tg(угол) = противолежащий катет / прилежащий катет.
Тригонометрические функции синус, косинус и тангенс широко используются в различных областях, таких как физика, инженерия и компьютерная графика, для решения задач, связанных с тригонометрией и геометрией. Понимание синуса, косинуса и тангенса позволяет эффективно работать с углами и вычислять их значения без использования сложных формул.
Простой метод вычисления без сложных формул

Когда мы говорим о вычислении синусов, косинусов и тангенсов углов, обычно представляем себе сложные математические формулы, требующие использования специализированных функций или таблиц. Однако существует простой метод, который позволяет относительно точно вычислить значения этих тригонометрических функций без использования сложных формул.
Основная идея этого метода заключается в представлении угла в виде рациональной дроби и последовательном приближении его значения с помощью частичных сумм ряда Тейлора. Для этого необходимо использовать только четыре простые операции: сложение, вычитание, умножение и деление.
Процесс вычисления начинается с выбора приближения для значения угла, например, можно взять значения в интервале от 0 до π/4 (от 0 до 45 градусов). Затем используя ряд Тейлора для соответствующей тригонометрической функции (например, для синуса, косинуса или тангенса), мы последовательно приближаем значение угла с заданной точностью.
| Угол (градусы) | Синус | Косинус | Тангенс |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 15 | 0.2588 | 0.9659 | 0.2679 |
| 30 | 0.5 | 0.866 | 0.5774 |
| 45 | 0.7071 | 0.7071 | 1 |
Таблица выше показывает приближенные значения синусов, косинусов и тангенсов для нескольких углов. Используя простой метод вычисления без сложных формул, мы можем получить такие значения с относительно высокой точностью.
Необходимо отметить, что точность приближения будет увеличиваться с каждой итерацией вычислений. Этот метод может быть использован в различных областях, где требуется вычисление тригонометрических функций, и может быть особенно полезен, если использование специализированных функций не предусмотрено или требует больших вычислительных затрат.