Поиск корня числа является одной из базовых операций в математике. Определение корня числа может позволить нам найти значение, которое при возведении в квадрат даст исходное число. И хотя обычно для этой операции используют калькулятор, существует несколько методов и советов, которые позволяют нам найти корень числа вручную, без использования дополнительных инструментов.
Один из самых простых способов нахождения корня числа - это метод итераций (метод Ньютона). Суть метода заключается в последовательном приближении к искомому корню числа путем нахождения точного значения функции и ее производной в данной точке. Повторяя этот процесс несколько раз, мы можем получить все более точное значение корня числа.
Если вы предпочитаете более простой метод, вы можете использовать метод деления отрезка пополам (метод бисекции). Этот метод основан на принципе подбора двух чисел, находящихся по обе стороны от искомого корня числа, и последовательных деления отрезка пополам до тех пор, пока мы не найдем приближенное значение корня числа с заданной точностью.
Важно помнить, что поиск корня числа без калькулятора может быть трудоемкой задачей, особенно для больших чисел. Однако с помощью этих методов и советов вы сможете приблизиться к истинному значению корня числа и развить свои навыки в математических расчетах. Удачного поиска корня числа!
Методы и советы по нахождению корня числа без калькулятора

Нахождение корня числа без помощи калькулятора может быть полезным навыком, особенно если у вас нет доступа к вычислительным средствам или вы просто хотите проверить результаты собственных расчетов. Существуют различные методы, которые могут помочь вам найти приближенное значение корня числа.
1. Метод деления отрезка пополам
Один из наиболее простых методов нахождения корня числа – это метод деления отрезка пополам. Для этого вы выбираете два числа, одно из которых является верхней границей, а другое – нижней границей корня числа. Затем вы сравниваете значение средней точки между этими двумя числами с исходным числом и соответствующим образом сдвигаете границы. Продолжайте этот процесс до тех пор, пока значение средней точки не станет достаточно близким к искомому корню.
2. Метод тангенса
Другим методом нахождения корня числа является метод тангенса. В этом методе вы выбираете начальное приближение для корня числа и вычисляете соответствующий тангенс. Затем вы находите обратный тангенс от полученного значения и умножаете его на исходное приближение. Повторяйте этот процесс несколько раз, чтобы получить все более точные значения корня числа.
3. Метод Ньютона
Метод Ньютона – это итерационный метод для нахождения корня числа. В этом методе вы выбираете начальное приближение для корня числа и вычисляете касательную к кривой, представляющей функцию, у которой вы ищете корень. Затем вы используете пересечение этой касательной с осью x в качестве следующего приближения для корня числа. Повторяйте этот процесс несколько раз, чтобы приближаться к истинному значению корня.
Важно помнить, что все эти методы дадут вам только приближенное значение корня числа. Для полной точности требуется использование более сложных вычислительных методов.
Использование этих методов может быть полезно во многих областях, от математики и физики до инженерии и программирования. Нахождение корня числа без калькулятора поможет вам лучше понять математические концепции и развить навыки ручного вычисления.
Метод Деления отрезками
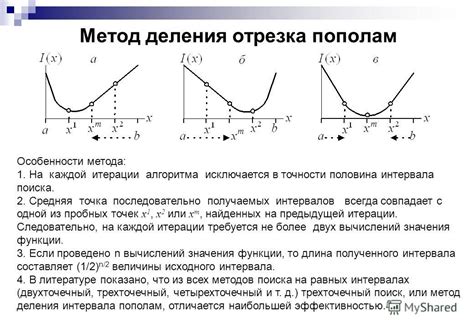
Принцип метода Деления отрезками заключается в следующем:
1. Задаем начальный отрезок, на котором мы ищем корень числа. Начальный отрезок должен содержать значение, близкое к корню.
2. Делим начальный отрезок пополам и находим значение функции в средней точке.
3. Если значение функции в средней точке близко к нулю, то это значение считается приближенным корнем. Если нет, то выбираем новый отрезок, содержащий значение функции противоположного знака.
4. Повторяем шаги 2-3, пока не достигнем заданной точности.
Метод Деления отрезками является достаточно простым и эффективным методом поиска корня числа. Он может быть использован в различных задачах, включая задачи из математики, физики, экономики и других областей науки.
Пример использования метода Деления отрезками:
Предположим, что нам нужно найти корень квадратный из числа 25. Зададим начальный отрезок [0, 10], так как значение квадратного корня 25 находится в этом диапазоне. После нескольких итераций мы найдем, что корень квадратный из числа 25 приближенно равен 5.
Метод Деления отрезками позволяет найти корень числа без использования калькулятора с заданной точностью. Однако он требует нескольких итераций и может быть неэффективным для больших значений числа.
Метод Итерации

Чтобы использовать метод итерации для поиска корня числа, нужно выбрать начальное приближение для корня и провести несколько итераций, чтобы приблизиться к истинному значению. Этот метод подразумевает использование математических формул и выражений, но его можно упростить до простого алгоритма.
Процесс поиска корня по методу итерации состоит из следующих шагов:
- Выбор начального приближения для корня.
- Вычисление значения функции в этой точке.
- Сравнение полученного значения с нулем.
- Корректировка значение приближения в зависимости от результата сравнения.
- Повторение шагов 2-4 до достижения достаточной точности.
Итеративный процесс продолжается до тех пор, пока значение функции на шаге не станет достаточно близким к нулю или достигнута достаточная точность. В результате получается приближенное значение корня исходного числа.
Метод итерации является одним из методов численного анализа, который широко применяется в различных областях, таких как математика, физика, экономика и технические науки. Он позволяет решать сложные математические задачи без использования калькулятора или других вычислительных устройств.
Метод Ньютона-Рафсона
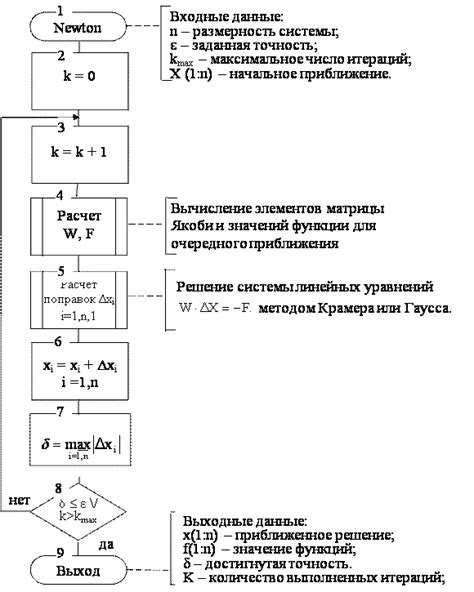
Основная идея метода заключается в следующем: мы начинаем с некоторого начального приближения к корню и выполняем последовательные итерации для уточнения значения. В каждой итерации мы используем значение функции и её производной, чтобы получить лучшую оценку корня.
Алгоритм метода выглядит следующим образом:
- Выбрать начальное приближение x0 для корня.
- Вычислить значение функции f(x) и её производной f'(x) в точке x0.
- Вычислить значение x1 по формуле: x1 = x0 - f(x0) / f'(x0).
- Повторять шаги 2 и 3, пока не достигнута необходимая точность.
Метод Ньютона-Рафсона сходится очень быстро и точно приближается к корню функции. Однако, следует помнить, что он требует знания производной функции, что может быть сложно или затратно в некоторых случаях. Также, начальное приближение может сильно влиять на сходимость метода.
Важно отметить, что при работе с методом Ньютона-Рафсона необходимо быть внимательными и проверять условия сходимости, чтобы избежать грубых ошибок и получить точный результат.