Расчет длины дуги прямой - это важный аспект в математике, геометрии и физике. Применение правильных методов и формул позволяет определить точное значение длины дуги прямой. В данной статье мы рассмотрим несколько простых приемов, которые помогут вам справиться с этой задачей быстро и легко.
Секрет точного расчета длины дуги прямой заключается в правильном использовании формул и учете всех необходимых параметров. В основе расчета лежит формула длины дуги, которая основана на угле между начальной и конечной точкой дуги, а также на радиусе окружности, в которую вписана эта дуга.
Для расчета длины дуги прямой можно использовать как простые математические формулы, так и компьютерные программы или онлайн-калькуляторы. Однако в этой статье мы рассмотрим исключительно ручной расчет для тех, кто хочет более полно разобраться в этой теме и освоить простые методы расчета самостоятельно.
Методы расчета длины дуги прямой: точные расчеты, секреты и советы
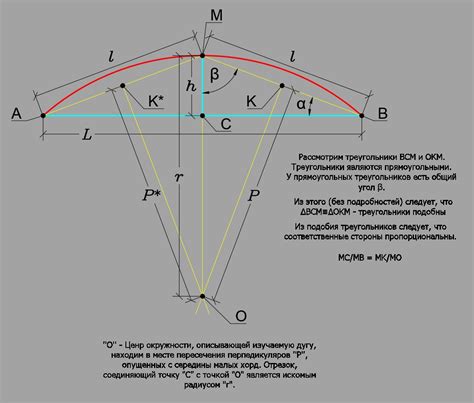
Одним из наиболее точных методов расчета длины дуги является применение тригонометрической формулы. Для этого нужно знать длину отрезка прямой и угол, под которым данный отрезок составляет с осью абсцисс. Тригонометрическая формула дает точный результат, однако требует знания тригонометрических функций и угла в радианах.
Другой метод, который позволяет достаточно точно рассчитать длину дуги прямой, это аппроксимация дуги прямой отрезками. Для этого прямую разбивают на малые отрезки, после чего рассчитывается длина каждого отрезка с использованием формулы длины отрезка. Затем все полученные значения складываются, получая примерное значение длины дуги.
Секретом точного расчета длины дуги прямой является использование численных методов, таких как метод Монте-Карло или метод Симпсона. Эти методы позволяют получить более точную оценку длины дуги, основываясь на анализе большого количества точек на прямой.
Когда рассчитывается длина дуги прямой, важно помнить о некоторых советах. Во-первых, необходимо учитывать единицы измерения. Если прямая задана в метрах, а угол в градусах, необходимо привести все к одним единицам измерения. Во-вторых, важно применять подходящие формулы и методы для расчета, учитывая особенности задачи. В-третьих, стоит проверять полученный результат с использованием других методов, чтобы убедиться в его точности.
В итоге, расчет длины дуги прямой может быть выполнен с использованием тригонометрических формул, аппроксимации или численных методов. Каждый из этих подходов имеет свои преимущества и недостатки, поэтому выбор метода зависит от конкретной задачи и требуемой точности.
Простая формула для радиуса и угла
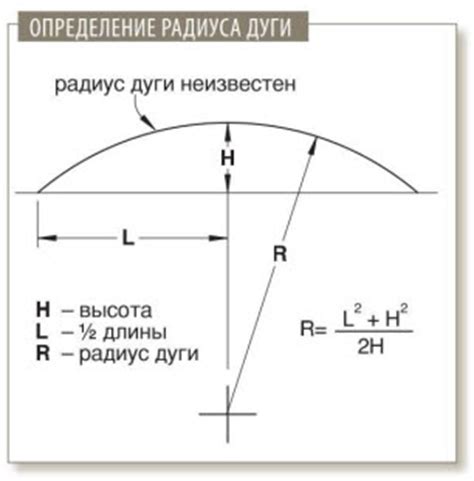
Если вам необходимо рассчитать длину дуги прямой, вы можете воспользоваться простой формулой, использующей радиус и угол.
Для этого вам понадобится знать радиус окружности, на которой находится вся дуга, а также угол, образуемый этой дугой. Радиус обозначается символом R, а угол - символом α.
Формула для расчета длины дуги S выглядит следующим образом:
S = R * α
Где S - длина дуги прямой, R - радиус окружности, α - угол, образуемый дугой.
Пользуясь этой простой формулой, вы сможете легко и быстро рассчитать длину дуги прямой. Учтите, что угол α должен быть выражен в радианах. Если у вас угол выражен в градусах, необходимо преобразовать его в радианы, умножив на π и разделив на 180.
Использование геометрии для расчета длины дуги
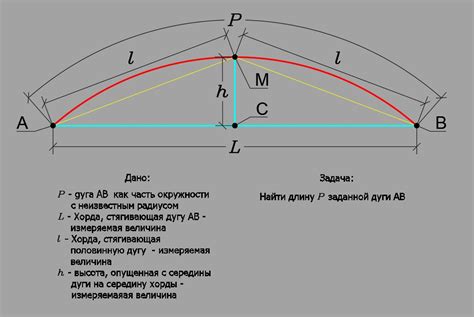
Геометрия предоставляет простые методы для точного расчета длины дуги прямой. Один из таких методов - использование формулы длины дуги, которая основывается на радиусе и углу дуги.
Формула длины дуги:
- Для измерения в радианах: длина_дуги = радиус * угол_дуги
- Для измерения в градусах: длина_дуги = (радиус * угол_дуги * π) / 180
Таким образом, для расчета длины дуги необходимо знать радиус и угол дуги. Значение угла обычно задается в градусах, но, если это нужно, его можно преобразовать в радианы с помощью формулы радианы = (градусы * π) / 180.
При расчете длины дуги следует обратить внимание на единицы измерения. Например, если радиус дан в метрах, а угол задан в радианах, то и длина дуги будет выражена в метрах.
Использование геометрии для расчета длины дуги позволяет получить точные значения и оценить геометрические характеристики прямой. Это важный инструмент для специалистов, занимающихся конструированием и расчетами в различных областях.
Надежные методы из математического анализа

Один из таких методов - использование интеграла для расчета длины дуги. Интеграл позволяет учесть все детали кривой и получить точный результат. Для расчета длины дуги прямой мы можем использовать следующую формулу:
| Формула | Описание |
|---|---|
| L = ∫[a,b] √(1 + (f'(x))^2) dx | Длина дуги прямой |
где a и b - начальная и конечная точки дуги прямой, f'(x) - производная функции, описывающей прямую.
Данный метод основан на фундаментальном принципе математического анализа - определении длины кривой как интеграла. Интеграл позволяет учесть все возможные изменения кривой и дает наиболее точный результат.
Использование надежных методов из математического анализа для расчета длины дуги прямой поможет получить точные результаты и избежать погрешностей, которые могут возникнуть при использовании приближенных формул. Отличительной особенностью этих методов является их точность и универсальность, что делает их незаменимыми во многих областях науки и техники.
Вычисление с помощью тригонометрии и косинусов
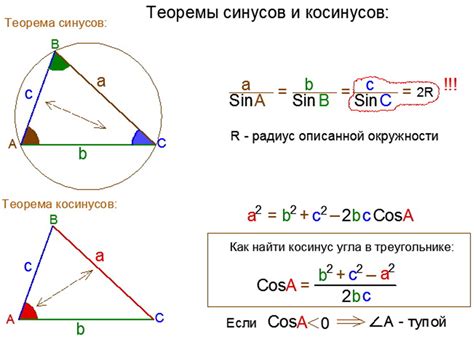
Один из простых методов расчета длины дуги прямой основан на использовании тригонометрии и косинусов. Этот метод позволяет получить приближенное значение длины дуги прямой без необходимости проведения точных расчетов.
Для вычисления длины дуги прямой с помощью тригонометрии и косинусов необходимо знать угол наклона прямой к оси X и длину самой прямой. Зная эти данные, можно применить формулу:
Длина дуги прямой = √(длина прямой^2 + (длина прямой * тангенс угла наклона)^2)
В этой формуле используется тригонометрическая функция тангенс, которая выражается через косинус и синус:
тангенс угла наклона = синус угла наклона / косинус угла наклона
Таким образом, вычисление длины дуги прямой с помощью тригонометрии и косинусов сводится к нахождению косинуса угла наклона прямой к оси X, рассчитыванию тангенса и использованию формулы.
Этот метод позволяет получить приближенное значение длины дуги прямой, и он особенно полезен, когда нет возможности использовать более сложные и точные методы расчета. Однако, стоит помнить, что точность расчета зависит от точности измерения угла наклона и длины прямой.
Точные значения с использованием численного анализа
Для расчета длины дуги прямой с использованием численного анализа необходимо провести ряд точных вычислений. Этот метод позволяет получить наиболее точное значение, гарантирующее минимальную погрешность.
В первую очередь, необходимо разбить прямую на небольшие сегменты. Чем меньше сегментов, тем более точный будет расчет. Затем для каждого сегмента применяется метод численного интегрирования, такой как метод прямоугольников, метод тrapezoid или метод Симпсона. Применение этих методов позволяет численно интегрировать функцию, представляющую прямую, и получить значение длины дуги каждого сегмента.
Затем полученные значения длины дуги сегментов суммируются для получения итогового значения длины дуги прямой. Чем больше сегментов использовано, тем точнее будет полученный результат. Однако, необходимо найти баланс между точностью и временем вычисления, поскольку использование слишком большого количества сегментов может значительно замедлить расчет.
Для улучшения точности вычислений можно применить алгоритмы адаптивного численного интегрирования, которые позволяют автоматически выбирать оптимальное количество сегментов для каждого участка прямой в зависимости от требуемой точности. Такие алгоритмы учитывают динамику значений функции и позволяют экономить вычислительные ресурсы, оптимизируя количество сегментов для использования.
Однако, следует отметить, что численный анализ может быть довольно сложным и требует хорошего математического понимания и навыков программирования. Поэтому, при необходимости получения точных значений длины дуги прямой, рекомендуется обратиться к специализированным инструментам или программным пакетам, которые предоставляют реализацию алгоритмов численного интегрирования и упрощают процесс расчетов.
Секреты для более точных результатов

Расчет длины дуги прямой может быть сложной задачей, особенно при использовании простых методов. Однако, существуют некоторые секреты, которые помогут вам получить более точные результаты.
Вот несколько советов:
| 1 | Используйте более точные измерительные инструменты. |
| 2 | Закрепите прямую так, чтобы она не двигалась в процессе измерений. |
| 3 | Измеряйте несколько раз и усредните результаты, чтобы уменьшить ошибку. |
| 4 | Повторяйте расчеты несколько раз, чтобы проверить консистентность результатов. |
| 5 | Избегайте измерений в условиях, которые могут влиять на точность результатов (например, при наличии воздушных потоков). |
Следуя этим советам, вы сможете получить более точные и надежные результаты при расчете длины дуги прямой. Помните, что точность измерений играет важную роль в любой научной или инженерной работе, поэтому не стоит пренебрегать этими простыми секретами.
Советы по упрощению расчетов длины дуги прямой
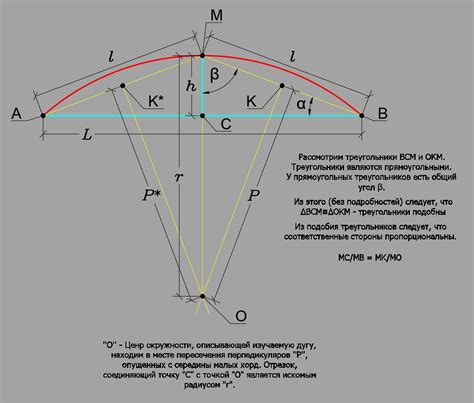
- Используйте простые формулы: для расчета длины дуги прямой, можно воспользоваться формулой, которая связывает длину дуги, радиусом окружности и углом между конечными точками дуги.
- Измерьте угол в радианах: для получения точного значения длины дуги прямой, угол необходимо измерять в радианах, так как формула для расчета длины дуги использует радианную меру угла.
- Упростите вычисления с помощью тригонометрических функций: используйте тригонометрические функции, такие как синус и косинус, чтобы упростить вычисления длины дуги прямой.
- Приближенные значения: если точность не является критической, можно использовать приближенные значения для радиуса окружности и угла между конечными точками, чтобы упростить расчеты.
- Используйте калькулятор: для более сложных расчетов длины дуги прямой, рекомендуется использовать калькулятор или специальные программы, которые автоматически выполняют вычисления.