Площадь геометрических фигур – одно из важных понятий, которое помогает решать задачи в различных областях науки и техники. Знание простых методов расчета площади треугольника, трапеции, параллелограмма и ромба может быть полезно как в повседневной жизни, так и в профессиональной деятельности.
Треугольник – базовая геометрическая фигура, которая имеет три стороны и три угла. Для расчета площади треугольника существует несколько простых методов. Одним из самых распространенных методов является использование формулы Герона, которая основывается на известных длинах сторон треугольника.
Трапеция – четырехугольник, у которого две стороны параллельны и две другие стороны не параллельны. Расчет площади трапеции также может осуществляться различными способами. Одним из наиболее простых методов является использование средней линии трапеции и ее высоты. Эта высота проходит перпендикулярно к двум параллельным сторонам и является основанием для расчетов.
Параллелограмм – четырехугольник, у которого противоположные стороны параллельны и равны. Площадь параллелограмма можно вычислить, умножив длину одной из сторон на высоту, опущенную на данную сторону. Это одна из самых простых формул для расчета площади данной фигуры.
Ромб – особый случай параллелограмма, у которого все стороны равны. Для расчета площади ромба необходимо знать длины его сторон и углы между ними. Простым методом является умножение длины одной из сторон на высоту, опущенную на данную сторону.
Методы расчета площади треугольника
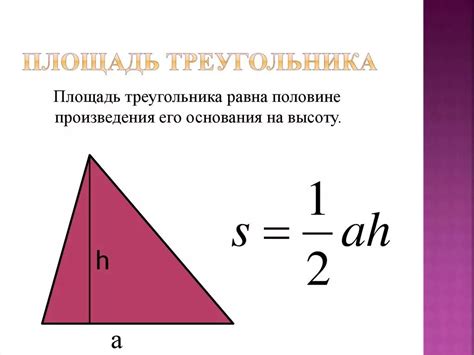
1. Метод половины основания и высоты: Если известна длина основания треугольника (a) и перпендикулярная к основанию высота (h), площадь треугольника (S) может быть вычислена по формуле: S = (a * h) / 2.
2. Метод половины произведения сторон на синус угла: Если известны длины двух сторон треугольника (a и b) и значение синуса угла между ними (sinA), площадь треугольника (S) может быть вычислена по формуле: S = (a * b * sinA) / 2.
3. Метод Герона: Если известны длины всех трех сторон треугольника (a, b и c), площадь треугольника (S) может быть вычислена по формуле Герона: S = sqrt(s * (s - a) * (s - b) * (s - c)), где s - полупериметр треугольника (s = (a + b + c) / 2).
Для расчета площади треугольника необходимо знать хотя бы одну известную сторону или угол, поскольку без этих данных невозможно определить его площадь.
Простой способ нахождения площади трапеции
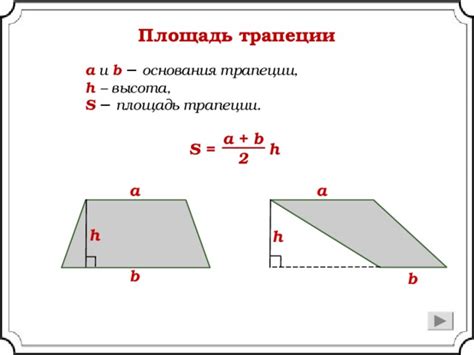
Для расчета площади трапеции, нам понадобятся длины двух параллельных сторон (оснований) и высота трапеции.
Формула для нахождения площади трапеции:
Площадь = (сумма оснований) * высота / 2
Чтобы применить эту формулу, необходимо измерить длины двух параллельных сторон, обозначить их как a и b, а также измерить высоту h.
Вот пример простого способа нахождения площади трапеции:
- Измерьте длину одного основания трапеции и обозначьте ее как a.
- Измерьте длину другого основания трапеции и обозначьте ее как b.
- Измерьте высоту трапеции и обозначьте ее как h.
- Примените формулу площади: Площадь = (a + b) * h / 2.
После выполнения этих шагов, вы получите значение площади трапеции.
Простой способ нахождения площади трапеции может быть полезен при выполнении различных задач по геометрии, строительству и других областях знаний.
Как найти площадь параллелограмма без сложных формул
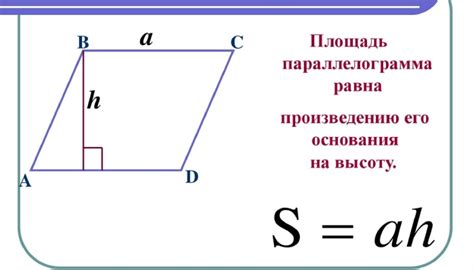
Для расчета площади параллелограмма нужно знать длину одной его стороны и высоту, опущенную на эту сторону. Высота параллелограмма - это расстояние между параллельными сторонами. Если вы не знаете высоту, ее можно легко найти, зная площади треугольников, образованных диагоналями параллелограмма.
Для нахождения площади параллелограмма можно применить следующий алгоритм:
- Найдите длину одной стороны параллелограмма и высоту, опущенную на эту сторону.
- Умножьте длину стороны на высоту.
Например, если сторона параллелограмма равна 5 см, а высота равна 3 см, то площадь равна 5 см * 3 см = 15 квадратных сантиметров.
Таким образом, вы можете легко найти площадь параллелограмма без сложных формул, используя простой и доступный метод.
| Название фигуры | Формула площади |
|---|---|
| Параллелограмм | Площадь = Длина стороны * Высота |
Легкий способ расчета площади ромба
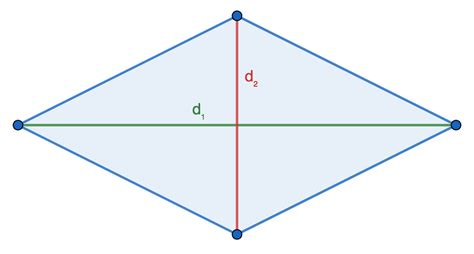
Площадь ромба можно вычислить с помощью простой формулы. Для этого необходимо знать длины двух диагоналей этой фигуры.
Формула для расчета площади ромба: S = (d1 * d2) / 2, где d1 и d2 - длины диагоналей ромба.
Применение этой формулы очень простое. Нужно всего лишь взять значения длин диагоналей и подставить их в формулу для получения площади ромба.
Давайте рассмотрим пример. Пусть длина одной диагонали ромба равна 8 см, а длина второй диагонали равна 6 см. Применяем формулу:
S = (8 * 6) / 2 = 48 / 2 = 24 см²
Таким образом, площадь ромба с данными параметрами равна 24 квадратным сантиметрам.
Как найти площадь треугольника по трем сторонам
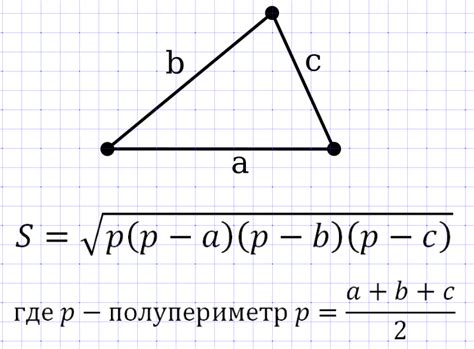
Площадь треугольника можно найти с использованием формулы Герона, которая позволяет расчитать площадь треугольника зная длины его сторон.
Для расчета площади треугольника по трем сторонам нужно выполнить следующие шаги:
- Найдите полупериметр треугольника. Для этого сложите длины всех сторон треугольника и разделите полученную сумму на 2.
- Используя найденный полупериметр и длины сторон треугольника, вычислите площадь треугольника по формуле Герона:
- После вычисления значения под корнем в формуле, получите окончательную площадь треугольника.
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника, a, b, c - длины сторон треугольника.
Таким образом, расчет площади треугольника по трем сторонам достаточно прост и позволяет найти точное значение площади без необходимости знать высоту треугольника.
Проще простого: формула для нахождения площади трапеции по основаниям
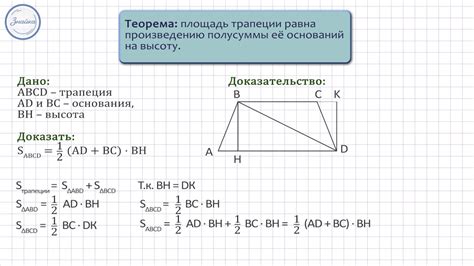
Формула для нахождения площади трапеции по основаниям:
Площадь = (сумма оснований * высота) / 2
Для использования данной формулы необходимо знать значения обоих оснований и высоту. Основания обычно обозначаются буквами a и b, а высота – буквой h.
Процесс вычисления площади трапеции по основаниям можно представить следующим образом:
- 1. Задайте значения оснований и высоты трапеции: a, b и h.
- 2. Просуммируйте длины оснований: сумма_оснований = a + b.
- 3. Умножьте сумму оснований на высоту: сумма_оснований * h.
- 4. Разделите полученное значение на 2: (сумма_оснований * h) / 2.
Полученное число будет являться площадью трапеции в заданных единицах измерения (например, квадратных метрах).
Теперь вы можете легко использовать данную формулу, чтобы вычислить площадь трапеции на практике. Удачных расчетов!