Геометрические фигуры - это объекты, которые мы ежедневно встречаем в нашей жизни. Знание и умение работать с этими фигурами является важным навыком, который поможет нам в различных ситуациях, начиная от ремонта и заканчивая строительством.
Расчет периметра и площади геометрических фигур является одной из основных задач, которые возникают в геометрии. Простые способы и формулы позволяют нам быстро и точно определить необходимые значения для любой фигуры.
Зная формулы для расчета периметра и площади фигур, мы сможем легко решать задачи, связанные с различными аспектами нашей повседневной жизни. Например, расчет площади комнаты поможет нам выбрать необходимое количество материалов для покрытия пола или стен, а расчет периметра забора позволит нам определить необходимую длину материала.
Эта статья представляет собой небольшой справочник, где вы найдете формулы и примеры расчета периметра и площади различных геометрических фигур, начиная от прямоугольников и овалов до треугольников и окружностей. Отличительной особенностью материала является его простота и доступность для любого читателя.
Методы расчета периметра геометрических фигур
1. Прямоугольник:
| Формула | Пример |
|---|---|
| Периметр = 2 * (длина + ширина) | Если длина = 4 см, ширина = 3 см, то периметр = 2 * (4 + 3) = 14 см |
2. Квадрат:
| Формула | Пример |
|---|---|
| Периметр = 4 * сторона | Если сторона = 5 см, то периметр = 4 * 5 = 20 см |
3. Треугольник:
| Формула | Пример |
|---|---|
| Периметр = сторона 1 + сторона 2 + сторона 3 | Если сторона 1 = 3 см, сторона 2 = 4 см, сторона 3 = 5 см, то периметр = 3 + 4 + 5 = 12 см |
4. Круг:
| Формула | Пример |
|---|---|
| Периметр = 2 * π * радиус | Если радиус = 6 см (π приближенно равно 3.14), то периметр = 2 * 3.14 * 6 = 37.68 см |
Расчет периметра геометрических фигур помогает определить длину границы фигуры и узнать, сколько длины необходимо для обхода ее.
Простые способы расчета площади геометрических фигур

Для простых геометрических фигур существуют простые способы расчета площади, которые даже школьнику будут понятны.
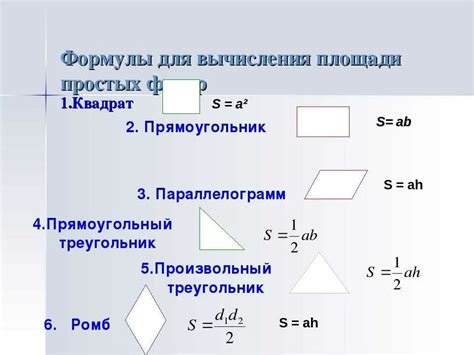
1. Площадь прямоугольника.
Для расчета площади прямоугольника нужно умножить длину одной из его сторон на длину другой стороны: S = a * b, где а и b – длины сторон прямоугольника.
2. Площадь квадрата.
Площадь квадрата равна квадрату его стороны: S = a^2, где а – длина стороны квадрата.
3. Площадь треугольника.
Для расчета площади треугольника можно использовать формулу Герона: S = √(p * (p-a) * (p-b) * (p-c)), где p – полупериметр треугольника (сумма длин всех его сторон, деленная на 2), а, b, c – длины сторон треугольника.
4. Площадь круга.
Площадь круга равна произведению квадрата радиуса на число π (пи): S = π * r^2, где r – радиус круга, π – приближенное значение константы, равное примерно 3,14159.
5. Площадь параллелограмма.
Площадь параллелограмма равна произведению длины одной из его сторон на длину высоты, опущенной на эту сторону: S = a * h, где a – длина стороны параллелограмма, h – длина высоты, опущенной на эту сторону.
Это лишь небольшой перечень простых способов расчета площади различных геометрических фигур. Зная эти формулы, можно легко определить площадь любой фигуры и решать задачи по геометрии.