Тангенс - это одна из тригонометрических функций, которая позволяет определить отношение противоположного и прилежащего катетов прямоугольного треугольника. В математике и физике тангенс широко используется, и понимание его принципа вычисления является важным аспектом для различных вычислений.
Вычисление тангенса угла может оказаться довольно простым, если вы знаете основные формулы и правила. Существует несколько способов вычисления тангенса: с помощью таблиц или калькулятора, а также с использованием геометрических и тригонометрических свойств.
Первый способ - это использование таблицы значений тангенсов. Таблица содержит предварительно вычисленные значения тангенсов различных углов. Вы можете найти соответствующий угол в таблице и использовать его тангенс для вашего расчета.
Второй способ - это использование калькулятора. Современные калькуляторы, как правило, имеют специальную функцию для вычисления тангенса угла. Вам просто нужно ввести градусы угла и нажать соответствующую кнопку. Калькулятор самостоятельно выполнит вычисления и выдаст результат.
Третий способ - это использование геометрических и тригонометрических свойств. Например, если у вас есть прямоугольный треугольник, вы можете вычислить тангенс угла, разделив величину противоположного катета на прилежащий катет. Можно также использовать тригонометрические формулы для вычисления тангенса через синус и косинус угла.
Поэтому, если вам потребуется вычислить тангенс угла, у вас есть несколько простых способов доступных для использования. Выберите подходящий метод в зависимости от ваших потребностей и навыков!
Преимущества вычисления тангенса угла
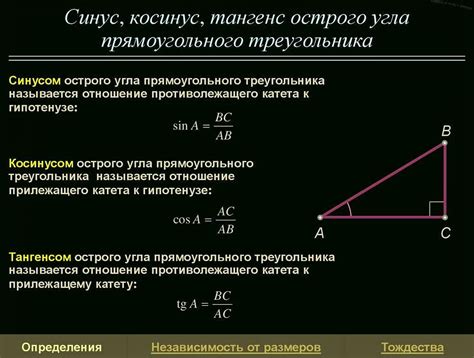
2. Важность в геометрии: Тангенс угла является важным инструментом в геометрии, поскольку позволяет определить угол между прямой и осью абсцисс на плоскости. Это позволяет решать задачи, связанные с построением треугольников и решением прямых и плоскостей.
3. Приложения в физике и инженерии: Тангенс угла широко используется в физике и инженерии для решения различных задач и расчетов. Например, в механике он может быть использован для вычисления сил, или для определения угла отражения света при падении на поверхность.
4. Демонстрация свойств угла: Тангенс угла позволяет исследовать различные свойства угла, такие как его наклонность, положение и взаимосвязь с другими углами. Это позволяет лучше понять структуру и характеристики геометрических фигур и форм.
5. Решение тригонометрических уравнений: Тангенс угла может быть использован для решения тригонометрических уравнений и нахождения неизвестной величины. Это особенно полезно при решении задач, требующих научных расчетов и моделирования.
В целом, вычисление тангенса угла имеет множество преимуществ и широкий спектр приложений в различных областях знаний. Оно позволяет решать задачи тригонометрии, геометрии, физики и других наук, а также исследовать свойства и структуры углов и фигур.
Тангенс угла и его значение в геометрии
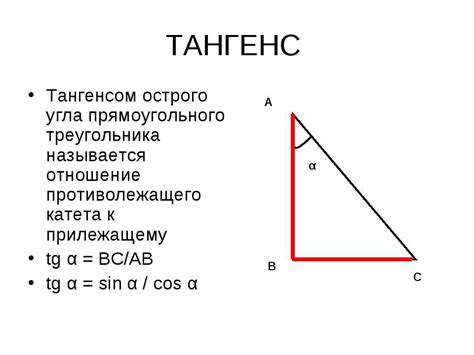
Значение тангенса угла может быть выражено численно или в виде десятичной дроби. Оно зависит от значения самого угла, поскольку тангенс является тригонометрической функцией.
Тангенс угла широко используется в геометрии для решения различных задач, таких как определение высоты, длины стороны или нахождения неизвестных углов в треугольнике. Он также имеет множество приложений в науке и технике.
Для нахождения тангенса угла можно использовать различные методы, включая таблицы тангенсов, специальные калькуляторы, математические формулы или программное обеспечение.
В общем случае, чтобы вычислить значение тангенса угла, нужно поделить значение синуса угла на косинус угла. Это можно сделать с помощью соответствующих тригонометрических функций или калькулятора.
Знание значения тангенса угла в геометрии позволяет решать различные задачи, связанные с треугольниками и углами. Кроме того, оно полезно для понимания основных принципов тригонометрии и математики в целом.
- Тангенс угла позволяет определить отношение противоположной и прилежащей сторон треугольника.
- Значение тангенса угла может быть представлено численно или в десятичной форме.
- Вычисление тангенса угла может быть выполнено с использованием различных методов и инструментов.
Таким образом, тангенс угла является важной геометрической функцией, которая находит широкое применение в различных областях науки и техники. Знание тангенса угла позволяет решать задачи, связанные с треугольниками, и имеет большое значение в геометрии и математике в целом.
Формула для вычисления тангенса угла
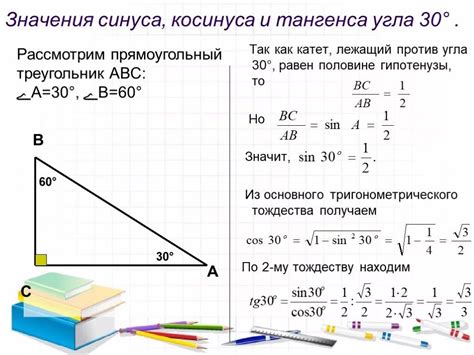
тангенс угла = противолежащая сторона / прилежащая сторона
Для расчета тангенса угла в градусах необходимо знать длины соответствующих сторон треугольника. Противолежащая сторона - это сторона, противостоящая углу, а прилежащая сторона - это сторона, прилегающая к углу.
Например, если известна противолежащая сторона треугольника и прилежащая сторона, то можно применить формулу для вычисления тангенса угла и получить значение этого тригонометрического отношения.
Зная тангенс угла, можно определить его величину и применить для решения различных задач в геометрии, физике, технике и других областях науки и практики.
Простые шаги по вычислению тангенса угла в градусах

Шаг 1: Возьмите угол, для которого требуется найти тангенс, и определите его значение в градусах. Назовем это значение α.
Шаг 2: Преобразуйте значение угла в радианы, умножив его на π/180. Обозначим это преобразованное значение как θ.
Шаг 3: Используя тригонометрический круг или таблицу тангенсов, найдите тангенс угла θ. Обозначим этот тангенс как tan(θ).
Шаг 4: Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету, то мы можем сказать, что tan(θ) = противолежащий катет / прилежащий катет.
Шаг 5: Подставьте значение угла в градусах (α) вместо противолежащего катета и полученный результат подставьте вместо прилежащего катета. Таким образом, вы получите искомое значение тангенса угла в градусах.
Используя эти простые шаги, вы сможете вычислить тангенс угла в градусах без необходимости использовать сложные математические формулы или калькуляторы. Удачных вычислений!
Как использовать тангенс для решения геометрических задач

Для использования тангенса в геометрических задачах, сначала необходимо измерить угол. Как правило, угол задается в градусах. Затем можно использовать тригонометрические таблицы или калькуляторы для вычисления тангенса этого угла.
Рассмотрим применение тангенса на примере геометрической задачи. Предположим, что нам нужно найти длину отрезка AB на плоскости, зная угол α между отрезком AB и осью X, а также длину отрезка AC, параллельного оси Y. В этом случае мы можем использовать тангенс, чтобы связать эти величины.
Для вычисления тангенса угла α можно использовать следующую формулу:
тангенс α = длина отрезка AC / длина отрезка AB
Теперь, используя известные данные, мы можем легко вычислить длину отрезка AB:
длина отрезка AB = длина отрезка AC / тангенс α
Применение тангенса в геометрических задачах может значительно упростить решение и помочь определить неизвестные величины. Важно помнить, что эта функция имеет свои ограничения и может быть использована только для определенных типов треугольников или углов.
Сравнение вычисления тангенса угла в градусах и радианах
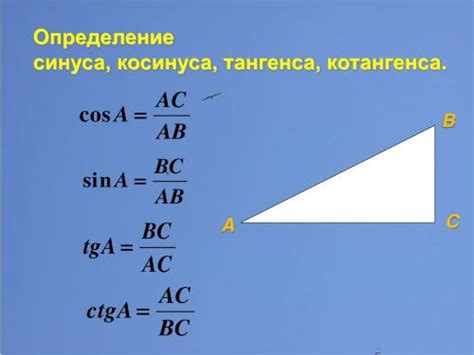
Тангенс угла можно вычислить как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Однако, вместо того чтобы использовать произвольный треугольник, можно воспользоваться удобной формулой для вычисления тангенса:
тангенс угла (в градусах) = противоположная сторона / прилежащая сторона
Если угол задан в радианах, то формула для вычисления тангенса будет следующей:
тангенс угла (в радианах) = sin(угол) / cos(угол)
Имеется небольшое отличие в вычислении тангенса угла, в зависимости от того, задан ли угол в градусах или радианах. Для нахождения тангенса угла в градусах достаточно разделить противоположную сторону на прилежащую сторону. В то же время, для того чтобы найти тангенс угла в радианах, необходимо сначала вычислить синус и косинус угла, а затем разделить синус на косинус.
Для удобства вычисления тангенса угла в радианах можно использовать таблицу значений синусов и косинусов. Такая таблица поможет сразу определить значения синуса и косинуса для заданного угла в радианах, из которых затем можно найти тангенс.
| Угол (в радианах) | Синус | Косинус | Тангенс |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| π/6 | 1/2 | √3/2 | √3/3 |
| π/4 | √2/2 | √2/2 | 1 |
| π/3 | √3/2 | 1/2 | √3 |
| π/2 | 1 | 0 | ∞ |
Однако, необходимо помнить, что тангенс угла в результатах вычислений может принимать значение бесконечности или быть неопределенным для некоторых углов.
Таким образом, для простых вычислений тангенса угла рекомендуется использовать его значение в градусах, поскольку это позволяет избежать лишних вычислений и использования таблицы значений синусов и косинусов.
Популярные ошибки при вычислении тангенса угла
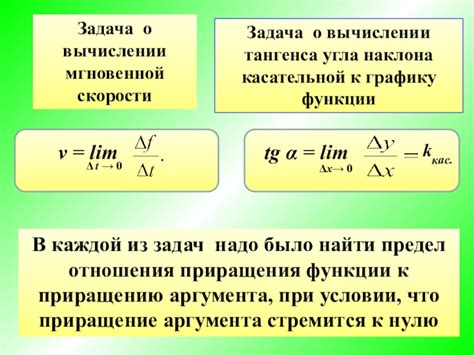
Вычисление тангенса угла может быть нетривиальной задачей, особенно для новичков в математике. В процессе вычислений допускаются различные ошибки, которые могут привести к неверным результатам. В этом разделе мы рассмотрим несколько популярных ошибок при вычислении тангенса угла.
- Не правильно указание единиц измерения угла. Тангенс - это отношение противоположной и прилежащей стороны треугольника. Для правильного вычисления тангенса необходимо убедиться, что угол указан в правильных единицах измерения. Например, если угол задан в градусах, необходимо использовать тангенс градусов.
- Использование неправильной формулы. Существует несколько различных формул для вычисления тангенса угла в зависимости от известных данных. Ошибка может быть допущена при выборе и использовании неправильной формулы. Поэтому перед вычислением тангенса угла необходимо определить, какая формула будет применяться в данном конкретном случае.
- Неправильное округление результатов. При вычислении тангенса угла может возникнуть необходимость округления результатов до определенного числа знаков после запятой. Ошибка может произойти при неправильном округлении результатов, что может привести к неточным значениям тангенса.
- Использование неправильных единиц измерения для входных данных. Важно убедиться, что правильные единицы измерения используются для входных данных, таких как длины сторон треугольника или углы.
- Ошибки при работе с углом, равным 90 градусов. Значение тангенса угла 90 градусов равно бесконечности. Ошибка может возникнуть при попытке вычислить тангенс 90 градусов, не учитывая эту особенность.
Избегайте этих популярных ошибок, чтобы получить точные результаты при вычислении тангенса угла. Знание правильных методов и формул для вычисления тангенса угла поможет вам избежать этих ошибок и получить точные результаты.