В мире геометрии эллипс - это фигура, которая возникает при пересечении конуса плоскостью под углом, не равным нулю, к оси конуса. Интерес к таким фигурам возник уже много веков назад и ученые до сих пор продолжают исследовать их свойства. Одним из важных аспектов изучения эллипсов является проведение проверки их соответствия определенным правилам и критериям.
Существует несколько методов проверки эллипса. Один из наиболее распространенных и простых - аналитический метод. Он основан на математическом аппарате и позволяет определить по заданным координатам вершин и центра эллипса, соответствует ли фигура определенным условиям. Для этого используются различные формулы и уравнения, которые учитывают координаты точек и параметры эллипса.
Правила проверки эллипса также включают геометрический подход. В этом случае, для определения соответствия фигуры эллипсу, проводят различные измерения и вычисления, которые отражают геометрические свойства эллипса. Например, можно измерить длины полуосей, углы и радиусы кривизны и сравнить их с определенными значениями для эллипсов.
Проведение проверки эллипса важно для множества областей науки и техники. Например, в астрономии эллипсы используются для описания орбит планет и спутников, а в инженерии - для создания оптимальных форм конструкций и механизмов. Правильная проверка эллипса помогает достичь точности и надежности в различных задачах и приложениях.
Проверка эллипса: методы для достижения точности

Для достижения точности в проверке эллипса существует ряд методов, которые позволяют более точно определить форму эллипса и его параметры. Рассмотрим некоторые из них:
1. Метод наименьших квадратов
Данный метод основан на минимизации суммы квадратов отклонений между измеренными точками и их предполагаемыми координатами на эллипсе. Для этого используется математическая оптимизация, которая позволяет получить наилучшую аппроксимацию эллипса.
2. Метод эллипса наименьших квадратов
Этот метод является модификацией метода наименьших квадратов и основан на использовании параметрической модели эллипса. Задача заключается в определении коэффициентов такой модели, которая минимизирует сумму квадратов отклонений.
3. Метод Монте-Карло
Метод Монте-Карло основан на генерации большого количества случайных точек и проверке их принадлежности эллипсу. Чем больше точек попадает внутрь эллипса, тем точнее его форма считается. Этот метод позволяет получить вероятностную оценку для параметров эллипса.
4. Метод эллипсической маски
При выборе метода для проверки эллипса необходимо учитывать особенности конкретной задачи и доступные ресурсы. Комбинирование различных методов и использование современных алгоритмов обработки изображений позволяет достичь высокой точности в проверке эллипса.
Точное понимание эллипса для проверки различных объектов
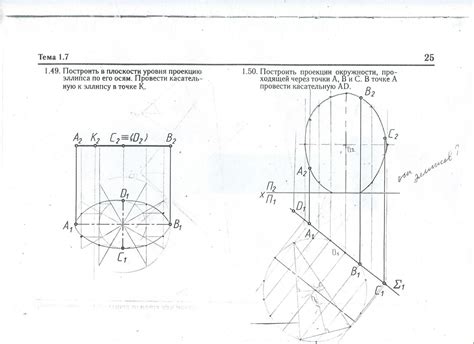
Прежде чем приступить к проверке объектов на соответствие эллипсу, необходимо иметь ясное и точное понимание этой геометрической фигуры.
Эллипс представляет собой плоскую кривую фигуру, ограниченную овалом, в котором два фокуса расположены на одной прямой, а сумма расстояний от любой точки к фокусам фиксирована. Главными характеристиками эллипса являются его большая полуось (а) и малая полуось (b), а также его центр (х0, y0).
Важно помнить, что проверка объектов на соответствие эллипсу требует точных математических вычислений и использования специальных алгоритмов. Использование правильных методов и правил позволяет достичь более точных результатов и уменьшить вероятность ошибок при проверке.
Таким образом, чтобы обеспечить точность и эффективность проверки объектов на соответствие эллипсу, необходимо иметь глубокое понимание этой геометрической фигуры, а также использовать правильные методы и правила. Только тогда можно быть уверенным в достоверности результатов проверки и использовать их в дальнейшем анализе и принятии решений.
Алгоритмы проверки эллипса: рационализация и ускорение процесса
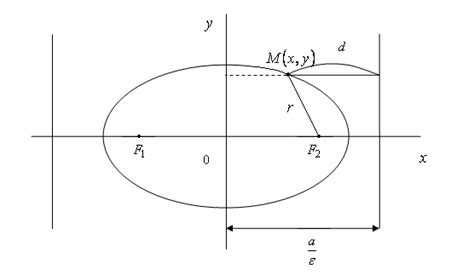
Для рационализации и ускорения процесса проверки эллипса были разработаны различные алгоритмы. Они позволяют провести проверку эффективно и точно.
Один из таких алгоритмов - алгоритм Фицгера - является классическим и широко используется для проверки эллипсов. Он основан на вычислении эллиптического интеграла второго рода и сравнении его с заранее заданным критерием. С помощью этого алгоритма можно определить, является ли данная фигура эллипсом или нет, с высокой точностью.
Еще одним эффективным алгоритмом является алгоритм Манинова - Хэрли. Он использует комбинированные подходы и позволяет проверить эллипс на соответствие определенному набору критериев, таким как отношение большой и малой полуоси, отношение площадей и т.д. Алгоритм Манинова - Хэрли позволяет провести проверку с высокой скоростью и точностью.
Другим эффективным алгоритмом является алгоритм Гаусса - Маркаса. Он основан на вычислении момента инерции эллипса и сравнении его с заданным значением. Алгоритм Гаусса - Маркаса позволяет провести проверку с высокой точностью и быстродействием.
Выбор конкретного алгоритма зависит от требуемой точности проверки и доступных ресурсов. Некоторые алгоритмы требуют большего объема вычислений, но обеспечивают более точные результаты, в то время как другие алгоритмы могут быть менее точными, но требуют меньшего объема вычислений.
Таким образом, использование оптимизированных алгоритмов проверки эллипса позволяет рационализировать и ускорить процесс проверки, с сохранением достаточной точности результатов. Правильный выбор алгоритма является важным шагом в анализе эллипсов и обеспечивает более эффективную работу с геометрическими фигурами.
Возможности компьютерного моделирования в проверке эллипса
Одной из возможностей компьютерного моделирования является визуализация эллипса и его параметров. С помощью графических средств можно создать трехмерную модель эллипса и анализировать его форму, размеры и расположение относительно других объектов.
Другой возможностью компьютерного моделирования является решение геометрических задач, связанных с проверкой эллипса. С использованием математических алгоритмов и вычислительных методов можно определить точки пересечения эллипса с другими геометрическими объектами, найти фокусы и вершины эллипса, а также провести анализ кривизны и симметрии.
Использование компьютерного моделирования также позволяет проводить численные эксперименты для проверки эллиптических уравнений и формул. Это особенно актуально при работе с большими объемами данных и сложными математическими моделями.
| Преимущества компьютерного моделирования в проверке эллипса: | Ограничения компьютерного моделирования в проверке эллипса: |
|---|---|
| Более точные результаты | Недостаточная точность при использовании приближенных моделей |
| Ускорение процесса проверки | Необходимость определения и калибровки параметров модели |
| Возможность анализа сложных геометрических задач | Необходимость специального программного обеспечения |
| Возможность работы с большими объемами данных | Ограниченные вычислительные ресурсы |
Важность правильного выбора параметров при проверке эллипса

При проверке эллипса на соответствие требуемым характеристикам и параметрам необходимо учитывать ряд ключевых факторов. В первую очередь, важно правильно определить основные параметры эллипса, такие как большая полуось, малая полуось, фокусное расстояние и эксцентриситет.
Выбор этих параметров должен основываться на конкретной задаче и требованиях к эллипсу. Например, если эллипс используется для моделирования орбиты планеты, то основные параметры будут зависеть от массы планеты, силы притяжения и других факторов, определяющих орбиту.
Для каждого случая выбор параметров должен быть обоснован и основываться на эмпирических данных или научных исследованиях. Неверный выбор параметров может привести к неверным результатам и неправильной интерпретации данных.
Кроме того, важно учитывать допустимое отклонение от требуемых параметров при проверке эллипса. Некоторые задачи могут требовать более высокой точности, в то время как для других достаточно более грубой оценки.
Весь процесс проверки эллипса на соответствие параметрам и характеристикам должен быть четко задокументирован и прозрачен. Это поможет избежать ошибок и спорных моментов при дальнейшей работе с эллипсом.
В итоге, правильный выбор параметров при проверке эллипса является важным этапом, который влияет на точность и достоверность получаемых результатов. Поэтому необходимо уделить этому вопросу достаточное внимание и обеспечить его правильное выполнение.
Нормы и стандарты для проведения проверки эллипса: что нужно знать
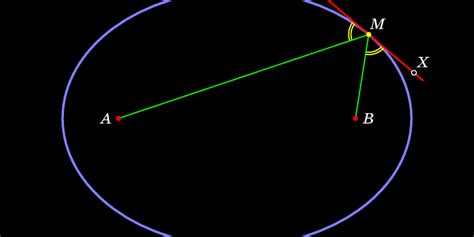
При проведении проверки эллипса, важно соблюдать нормы и стандарты, чтобы гарантировать достоверные результаты и соответствие установленным требованиям. Знание данных норм и стандартов позволит проводить проверку эллипса правильно и эффективно.
Один из важных стандартов, который необходимо учитывать при проверке эллипса, - это СТБ 855.0-2015 "Государственная метрологическая поверка. Объекты государственной метрологической поверки. Требования к документации и функциям служб поверки". Этот стандарт устанавливает требования к поверке оборудования и инструментов и регламентирует процедуры поверки.
Помимо стандарта СТБ 855.0-2015, следует учитывать также руководства и рекомендации, разработанные организациями, специализирующимися в области метрологии и проверки эллипса. Например, Международная академия эллипса (International Ellipse Academy) опубликовала свои рекомендации, в которых описываются современные методы и техники проверки эллипса.
При проведении проверки эллипса также важно учитывать национальные стандарты и нормативные документы. В большинстве стран существуют национальные стандарты, которые регламентируют требования к проведению проверки эллипса и калибровке оборудования.
Правильная интерпретация и применение норм и стандартов позволят избежать ошибок и обеспечить надежность и точность результатов проверки эллипса. При подготовке к проведению проверки эллипса следует ознакомиться с актуальными нормативными документами и учесть их требования.
Техники и советы для более эффективной проверки эллипса

Проверка эллипса может быть сложной задачей, но с помощью определенных техник и советов вы сможете провести ее более эффективно. В этом разделе мы рассмотрим несколько приемов, которые помогут вам достичь точного и надежного результата.
1. Используйте шаблонные изображения Для более практической проверки эллипса вы можете использовать шаблонные изображения, которые имеют известные параметры эллипса. С помощью таких изображений вы сможете сравнить результаты своей проверки и убедиться в их правильности. Вы можете найти такие изображения в интернете или создать их с помощью специальных графических программ. |
2. Проверьте все параметры эллипса Для точной и надежной проверки эллипса вы должны убедиться, что все его параметры правильно определены. Это включает в себя проверку длины осей, центра эллипса, угла наклона и других характеристик. Проверьте каждый параметр отдельно и убедитесь, что он соответствует требуемым значениям. |
3. Используйте геометрические методы Для более точной и эффективной проверки эллипса вы можете использовать геометрические методы. Например, вы можете использовать теорему Пифагора для проверки соотношения между полуосями эллипса. Также вы можете использовать уравнения эллипса для проверки его параметров. Использование геометрических методов позволяет получить более точные результаты и избежать ошибок. |
4. Проверьте эллипс на графике Если у вас есть возможность, визуализируйте эллипс на графике. Это позволит вам лучше понять его форму и параметры. Систематически проверяйте график на соответствие ожидаемым характеристикам эллипса. Если вы обнаружите расхождение, проверьте все параметры еще раз и убедитесь, что они правильно определены. |
5. Проверьте эллипс на аппроксимацию Иногда необходимо проводить проверку эллипса на аппроксимацию, особенно если он является результатом сложных вычислений или представляет собой аппроксимацию исходных данных. Для этого можно использовать различные методы, такие как наименьшие квадраты или метод наименьших отклонений. Проверка на аппроксимацию позволяет оценить точность и надежность эллипса. |
Следуя этим техникам и советам, вы сможете провести проверку эллипса более эффективно и достичь более точных результатов. Не забывайте также о самоконтроле и внимательности при выполнении проверки, чтобы избежать возможных ошибок.