Система линейных уравнений – это набор уравнений, содержащих неизвестные переменные и представляющих собой математическую модель, описывающую отношения между элементами системы. Одним из важных аспектов решения системы линейных уравнений является проверка и оценка совместности данной системы.
Система линейных уравнений может быть совместной, то есть иметь хотя бы одно решение, или несовместной, то есть не иметь ни одного решения. Каким образом можно определить совместность системы? Один из самых распространенных методов – это метод гауссовых исключений или метод приведения системы к ступенчатому виду. Получив ступенчатый вид системы, мы сможем определить, содержит ли система противоречивые уравнения, что свидетельствует о ее несовместности.
Помимо проверки совместности, важно также оценить количество решений системы линейных уравнений, если она является совместной. В данном случае, существует два возможных варианта – система может иметь единственное решение, или же бесконечное множество решений. Для этого нам необходимо проанализировать количество уравнений и количество неизвестных переменных в системе. При наличии равного количества уравнений и неизвестных, система, как правило, имеет единственное решение. В случае, когда количество уравнений меньше количества неизвестных, система, как правило, имеет бесконечное количество решений.
Проверка совместности системы линейных уравнений
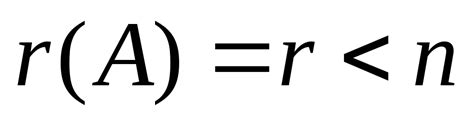
Существует несколько способов проверки совместности системы линейных уравнений. Один из них - применение метода Гаусса. Для этого систему заносят в расширенную матрицу, которая представляет собой таблицу, в которой уравнения системы записаны одно под другим, а справа от них расположены свободные члены.
После этого применяют элементарные преобразования строк матрицы с целью приведения ее к ступенчатому виду. Если на последнем этапе в ступенчатом виде матрица оказывается упрощенной и не содержит строки, в которой все элементы равны нулю, то система называется совместной. В противном случае, если матрица содержит пустую строку и хотя бы один ненулевой свободный член, система называется несовместной.
Другой способ проверки совместности - вычисление определителя матрицы коэффициентов системы. Если определитель равен нулю, то система несовместна. Если определитель не равен нулю, то система совместна. Определитель матрицы считается путем вычисления разности произведений элементов главной диагонали и побочной диагонали матрицы.
Таким образом, проверка совместности системы линейных уравнений является важным шагом в решении задач, связанных с этой темой. Она позволяет определить, существует ли общее решение системы и упрощает последующие действия при нахождении этого решения.
Понятие совместности и несовместности системы

Одним из важных понятий, связанных с системой линейных уравнений, является совместность. Система называется совместной, если существуют значения неизвестных, которые удовлетворяют всем уравнениям системы. Иначе, система называется несовместной.
Совместность системы можно определить при помощи метода единственного решения, метода отсутствия решений или метода бесконечного количества решений. Если система имеет единственное решение, то она совместна. Если система не имеет решений, то она несовместна. Если система имеет бесконечное количество решений, то она также совместна.
Для определения совместности системы линейных уравнений используется метод гаусса. Он позволяет привести систему к треугольному или ступенчатому виду. При этом, если в системе появляются противоречивые уравнения (например, 0 = 1), то система является несовместной. Если противоречий не возникает, то система совместна.
Понятие совместности и несовместности системы линейных уравнений является фундаментальным в алгебре. Оно позволяет определить, существует ли решение системы, и какое именно решение она имеет.
Критерии оценки системы на совместность
Система линейных уравнений называется совместной, если существует хотя бы одно такое решение, которым удовлетворяют все уравнения системы. Для оценки совместности системы возможно использовать следующие критерии:
1. Критерий Крамера. Если определитель основной матрицы системы равен нулю, система может иметь бесконечное число решений или не иметь их вовсе.
2. Ранг основной матрицы. Если ранг основной матрицы системы меньше числа неизвестных, то система может иметь бесконечное число решений или не иметь их вовсе.
3. Совместность однородной системы. Если однородная система имеет ненулевое решение, то она всегда совместна.
4. Совместность неоднородной системы. Если неоднородная система имеет хотя бы одно решение, то она всегда совместна. Если неоднородная система не имеет решений, то она несовместна.
Знание критериев оценки системы на совместность позволяет провести анализ и определить возможность нахождения решений системы линейных уравнений. Это важный этап при работе с системами уравнений и может помочь облегчить последующее решение задачи.
Способы решения системы линейных уравнений

Существует несколько способов решения системы линейных уравнений, в зависимости от ее особенностей и размерности.
1. Метод подстановки. Этот способ применяется в случае, когда система состоит из двух уравнений с двумя неизвестными. Для решения системы сначала находим значение одной неизвестной из одного уравнения, а затем подставляем его во второе уравнение и находим вторую неизвестную.
2. Метод равноаппроксимационного деления нацело. Этот метод используется для систем с большим количеством уравнений. Он основан на преобразовании системы уравнений в вид, где на месте неизвестных стоят целочисленные коэффициенты. Затем система делится по модулю некоторого числа и решается с помощью метода Гаусса.
3. Метод Крамера. Этот метод применяется, когда система состоит из n уравнений с n неизвестными. Для решения системы находим определитель основной матрицы системы и определители матриц, полученных заменой каждого столбца основной матрицы на столбец свободных членов. Затем находим значения неизвестных, деля каждый из найденных определителей на определитель основной матрицы.
4. Метод Гаусса. Этот метод применяется для систем с произвольным числом уравнений и неизвестных. Он основан на последовательном преобразовании системы уравнений с помощью элементарных преобразований до приведения ее к треугольному или ступенчатому виду. Затем из приведенной системы находим значения неизвестных.
Выбор метода решения системы линейных уравнений зависит от набора уравнений и их особенностей. Каждый метод имеет свои преимущества и недостатки, и для определенных систем один метод может быть более эффективным или удобным, чем другой.
Примеры применения проверки и оценки системы
Финансовое планирование. При составлении бюджета на предстоящий год, предприятия и организации используют системы линейных уравнений для моделирования и прогнозирования финансовых потоков. Проверка и оценка решений системы позволяют выявить возможные расхождения и корректировать бюджетные показатели.
Анализ данных. В науке и исследованиях системы линейных уравнений применяются для анализа и представления данных. Проверка и оценка решений системы помогают установить степень достоверности и точности полученных результатов.
Инженерные расчеты. В инженерных расчетах системы линейных уравнений широко применяются для моделирования и оптимизации различных процессов и систем. Проверка и оценка решений системы позволяют убедиться в правильности и надежности полученных результатов.
Это лишь несколько примеров использования проверки и оценки системы линейных уравнений. Однако они демонстрируют широкий спектр областей, в которых данная техника является полезной и неотъемлемой частью работы.