Главная » Интересно

Проверка и расчет алгоритмов магических квадратов 29

На чтение 7 мин Опубликовано Обновлено

Магический квадрат - это квадратная таблица, заполненная целыми числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Но среди множества всех возможных магических квадратов существует особый класс, известный как магический квадрат порядка 29. Его особенность заключается в том, что его размер составляет 29 на 29 ячеек.

Проверка и расчет алгоритмов магических квадратов порядка 29 является сложной задачей, требующей учета множества факторов. Для начала необходимо убедиться, что заданный квадрат действительно является магическим квадратом порядка 29. Для этого нужно посчитать сумму чисел в каждой строке, столбце и диагонали и сравнить полученные значения.

Однако, в случае магических квадратов порядка 29, даже проверка на сумму не является единственным критерием. Также необходимо учитывать ограничения на используемые числа - они должны быть целыми и лежать в определенном диапазоне. Кроме того, все числа должны быть уникальными, то есть в квадрате не должно быть повторяющихся чисел.

В расчете алгоритмов магических квадратов порядка 29 можно использовать различные методы и стратегии, включая перебор всех возможных вариантов, применение математических формул или использование эвристических алгоритмов. Какой метод выбрать - зависит от конкретной задачи и ее требований.

Что такое магические квадраты 29

Что такое магические квадраты 29

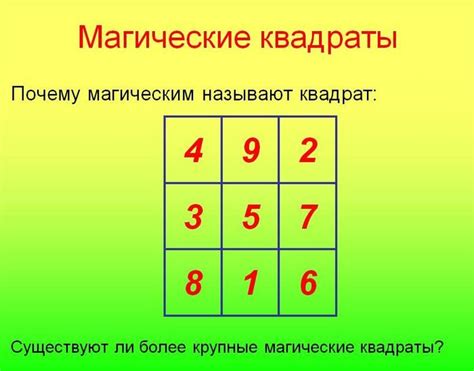
Магические квадраты 29 являются одной из разновидностей магических квадратов, которые уже с давних времен привлекали внимание ученых и математиков. Они представляют собой интерес не только в мире математики, но и в искусстве, астрологии и мистических верованиях.

Особенность магического квадрата 29 заключается в том, что его размерность равна 29, что делает его особо сложным для вычислений и решений. Такие квадраты имеют многочисленные комбинации чисел и требуют специальных алгоритмов и методов для их создания и проверки.

Использование магических квадратов 29 позволяет проводить различные эксперименты и исследования в области математики, логики и криптографии. Они также могут быть применены в головоломках и играх, развивая логическое мышление и способствуя развитию интеллекта.

Определение

Определение

Магические квадраты будоражат умы людей уже на протяжении многих веков. В разных культурах и эпохах они считались символами мистики, магии и числового совершенства.

Магические квадраты имеют различные размеры и могут быть составлены с использованием различных алгоритмов. Для создания магического квадрата необходимо соблюдать определенные правила, такие как: начинать с определенного числа, заполнять клетки таблицы по определенной методике и т.д.

Алгоритмы магических квадратов используются в различных областях математики, информатики, криптографии и даже в играх. Они представляют интерес для исследования и развития новых методов решения задач.

Как проверить магический квадрат

Как проверить магический квадрат
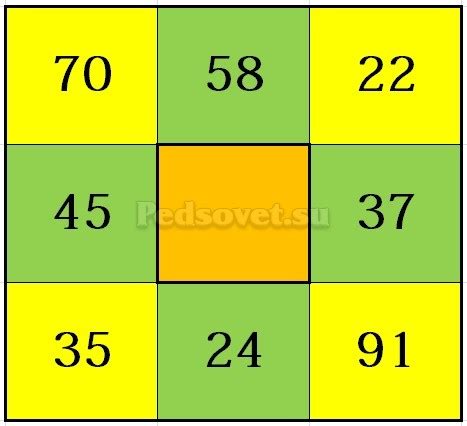
  1. Проверить суммы строк. Сложить все числа в каждой строке и сравнить полученные значения суммы.
  2. Проверить суммы столбцов. Сложить все числа в каждом столбце и сравнить полученные значения суммы.
  3. Проверить суммы диагоналей. Сложить все числа на главной диагонали и сравнить полученное значение суммы.
  4. Если все суммы равны между собой, то квадрат является магическим.

При проверке магического квадрата можно использовать математическую формулу для расчета суммы:

Сумма строк (столбцов, диагоналей) = (N * (N^2 + 1)) / 2

где N - размер стороны квадрата.

Таким образом, для 3x3 квадрата сумма строк, столбцов и диагоналей должна быть равна 15.

В случае если заданный квадрат не является магическим, необходимо проверить корректность введенных чисел и исправить ошибки.

Расчет алгоритмов

Расчет алгоритмов

Для создания магического квадрата порядка 29 необходимо провести расчеты согласно определенным алгоритмам. В данном разделе представлено описание этих алгоритмов и предлагается пример применения.

Один из основных алгоритмов - алгоритм Вильсона, который позволяет получить магический квадрат, используя только сложение и вычитание. Этот алгоритм состоит из следующих шагов:

  1. Создание двумерного массива размером 29x29 и заполнение его нулями.
  2. Выбор начальной позиции для числа 1 в середине первой строки.
  3. Заполнение оставшихся ячеек по следующему правилу: если текущая ячейка выходит за границы массива, то нужно вернуться на противоположную сторону;
  4. Если текущая ячейка уже содержит число, то нужно вернуться на ячейку выше и перейти в следующую колонку.
  5. Повторение шагов 3-4 до заполнения всех ячеек квадрата.

Пример применения алгоритма Вильсона для создания магического квадрата порядка 29:

3626642618849065266441817153226285109532334285171480418334616738
5452628526418362296109630628265323075326606644887811626237307
4803075452855842551652996311642627532660654261617842349114335
6726743762611043846965717335333253235017652467604368782266267
2629533854558262663426110594287457170174266752611065053123717
6045625561347082382702684263261734094266242611035218857639
2626884261105926223074076952611026269261102658263542112326
3435929926110265182611026317261103742611062021429532626
11069468362434516261105502611041964421426110405261102627426
110266771521102628526346294471102627261101242652163826190
2762611063461441026110261215852661767217326110261745395123
261105946022611026411173266311522611026110261106412631689
596261102611026110261102125726622611026370393288862981726
26641343266342611026110263062611070026372682167133526614
11071626180261102611026110631182261102625526886536775426
11026386263245182668497261102611026634652262614794347253110
5046932611021926110196261103226110439650174

Алгоритм для квадратов порядка 3

Алгоритм для квадратов порядка 3

Для создания магического квадрата порядка 3 существует простой способ.

1. Начните с заполнения первой строки квадрата числами 1, 2 и 3.

2. Для заполнения второй строки возьмите число, которое расположено над ней в первой строке, и разместите его справа от него. Повторите этот шаг для оставшихся двух чисел первой строки.

3. Для заполнения третьей строки возьмите число, которое находится в первой строке под текущим числом третьей строки, и разместите его ниже него. Повторите этот шаг для оставшихся двух чисел третьей строки.

4. После выполнения всех шагов получится магический квадрат порядка 3, в котором сумма чисел в каждой строке, столбце и диагонали будет одинаковой и равной 15.

Алгоритм для квадратов порядка 4

Алгоритм для квадратов порядка 4

Для создания магического квадрата порядка 4 мы можем использовать следующий алгоритм:

  1. Начинаем с пустого квадрата размером 4х4.
  2. Помещаем число 1 в центр верхней строки.
  3. Помещаем число 2 в ячейку, расположенную справа и выше предыдущей ячейки.
  4. Помещаем число 3 в ячейку, расположенную справа и ниже предыдущей ячейки.
  5. Помещаем число 4 в ячейку, расположенную справа и ниже предыдущей ячейки.
  6. Помещаем число 5 в ячейку, расположенную справа и ниже предыдущей ячейки.
  7. Помещаем число 6 в ячейку, расположенную справа и выше предыдущей ячейки.
  8. Помещаем число 7 в ячейку, расположенную справа и выше предыдущей ячейки.
  9. Помещаем число 8 в ячейку, расположенную справа и выше предыдущей ячейки.
  10. Помещаем число 9 в ячейку, расположенную справа и ниже предыдущей ячейки.
  11. Помещаем число 10 в ячейку, расположенную слева и выше предыдущей ячейки.
  12. Помещаем число 11 в ячейку, расположенную слева и выше предыдущей ячейки.
  13. Помещаем число 12 в ячейку, расположенную слева и выше предыдущей ячейки.
  14. Помещаем число 13 в ячейку, расположенную слева и ниже предыдущей ячейки.
  15. Помещаем число 14 в ячейку, расположенную слева и ниже предыдущей ячейки.
  16. Помещаем число 15 в ячейку, расположенную слева и ниже предыдущей ячейки.
  17. Помещаем число 16 в ячейку, расположенную слева и ниже предыдущей ячейки.

После выполнения всех шагов, мы получим магический квадрат порядка 4, в котором сумма чисел в каждой строке, столбце и диагонали будет одинакова. Такой алгоритм позволяет быстро и эффективно создать магический квадрат без использования сложных вычислений.

Алгоритм для квадратов порядка >4

Алгоритм для квадратов порядка >4

Для квадратов порядка более 4 существует особый алгоритм, который отличается от алгоритма для меньших квадратов. При использовании этого алгоритма требуется учитывать несколько дополнительных правил:

  1. Начинать заполнять квадрат с центральной ячейки верхнего ряда.
  2. Если в ячейке уже есть число, то следующее число нужно поместить в ячейку ниже текущей.
  3. Если в ячейке уже есть число и ниже ячейки нет свободной ячейки, то следующее число нужно поместить в ячейку под первой ячейкой текущего ряда.
  4. Если в ячейке уже есть число и под первой ячейкой текущего ряда тоже нет свободной ячейки, то следующее число нужно поместить в ячейку рядом с правым углом текущего ряда (последняя ячейка).

С использованием данных правил можно заполнить квадрат порядка от 5 до 29. Усложнение алгоритма для квадратов более высокого порядка объясняется необходимостью учесть большое количество находящихся в квадрате чисел и их расположение.

712131823
68171924
59162025
410152126
311142227

Применение алгоритма для квадратов порядка более 4 требует увеличенного времени выполнения и сложности расчетов, но при верной самой процедуре заполнения гарантирует получение корректного магического квадрата.

Примеры и приложения

Примеры и приложения

Магические квадраты 29 находят применение в различных областях, таких как:

Интеллектуальные игры. Магические квадраты используются в головоломках и играх, где необходимо заполнить квадрат таким образом, чтобы суммы чисел по строкам, столбцам и диагоналям были одинаковыми. Это тренирует логическое мышление и развивает интеллектуальные способности игрока.

Криптография. Магические квадраты могут использоваться в криптографических алгоритмах для генерации ключей шифрования. Строки и столбцы квадрата могут служить значением ключа, который будет использоваться для шифрования и дешифрования сообщений.

Искусство и дизайн. Магические квадраты могут быть использованы в дизайне интерьера, графическом дизайне и художественных работах. Они придают композиции гармоничность и симметрию, и могут служить основой для создания оригинальных и красивых паттернов.

Математические исследования. Магические квадраты изучаются в математическом анализе и теории чисел. Они привлекают внимание ученых своими необычными математическими свойствами и помогают исследовать особенности числовых последовательностей и комбинаторики.

Развлечения. Магические квадраты используются в развлекательных шоу, как элементы фокусов и фокусов с картами. Артисты и иллюзионисты используют их для создания впечатляющих и неожиданных иллюзий, которые заставляют зрителей удивляться и задумываться.

Оцените статью