Пустое множество – одно из основных понятий в математике, которое иногда вызывает путаницу. Термин может показаться противоречивым - какое множество может быть пустым? Однако, пустое множество является фундаментальным и неизбежным в математической логике и теории множеств.
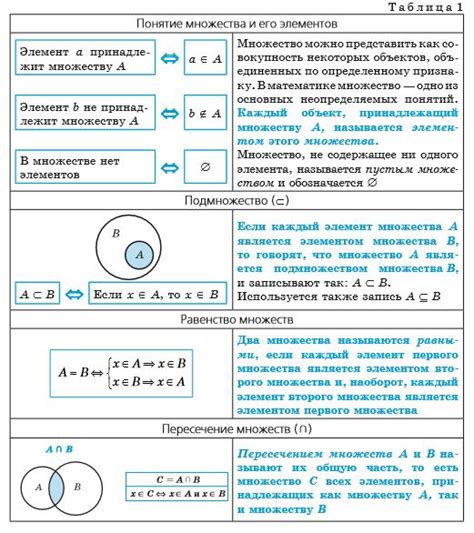
Пустое множество – это множество, не содержащее ни одного элемента. Оно обозначается символом ∅ или {} и называется также нулевым множеством или множеством без элементов. Формально, пустое множество можно определить как множество, которое не удовлетворяет ни одному условию, т.е. не существует таких элементов x, для которых x принадлежит этому множеству.
Пустое множество – это не пустое понятие. Оно играет важную роль в математике и используется во многих областях, включая теорию множеств, логику, теорию вероятностей и алгебру. Пустое множество часто используется для сохранения строгой логической формулировки математических утверждений и определений.
Пустое множество в математике: понятие и примеры
Пустое множество обозначается как ⌀ или {}.
Основная особенность пустого множества заключается в том, что оно является подмножеством любого другого множества. То есть, для любого множества A, пустое множество является его подмножеством.
Примеры использования пустого множества в математике:
- Решение уравнения, в котором не существует корней. Например, уравнение x^2 + 1 = 0 не имеет решений в области действительных чисел. В таком случае, можно сказать, что множество решений этого уравнения является пустым множеством.
- Объединение двух непересекающихся множеств. Например, пусть A = {1, 2, 3} и B = {4, 5, 6}. Если мы будем объединять множества A и B, то получим пустое множество, так как они не имеют общих элементов.
- Пустое множество также может использоваться в определении понятий или аксиом в математике. Например, аксиома пустого множества может быть использована для формулировки аксиомы о пустом множестве, которая утверждает, что для любого множества A, существует пустое множество, которое не содержит ни одного элемента из A.
Пустое множество является важным и полезным понятием в математике. Оно помогает нам формулировать определения, аксиомы и теоремы, а также рассматривать различные особенности множеств и их взаимодействия. Знание о пустом множестве и его свойствах является необходимым для понимания и работы с другими концепциями и теориями в математике.
Что такое пустое множество?

Наличие пустого множества имеет важное значение в теории множеств и других областях математики. Оно является базовым понятием, которое помогает определить другие понятия, такие как подмножество, объединение и пересечение множеств.
Пустое множество обозначается символом ∅ или { }.
| Понятие | Обозначение | Описание |
|---|---|---|
| Пустое множество | ∅ или { } | Множество, не содержащее никаких элементов. |
| Подмножество | A ⊆ B | Множество A является подмножеством множества B, если каждый элемент A также является элементом B. |
| Объединение | A ∪ B | Множество, содержащее все элементы из множества A и множества B. |
| Пересечение | A ∩ B | Множество, содержащее только общие элементы множества A и множества B. |
Использование пустого множества позволяет сформулировать определения и утверждения, которые будут верны в случае, когда множество не содержит элементов. Например, можно сказать, что для любого множества A, пересечение A и пустого множества равно пустому множеству: A ∩ ∅ = ∅.
Таким образом, пустое множество является важным понятием в математике и используется для определения других понятий и формулирования утверждений.
Примеры пустых множеств

Несмотря на то, что пустое множество не содержит элементов, оно является важным понятием в теории множеств и имеет свои применения.
Вот несколько примеров пустых множеств:
- Множество всех котов, которые умеют летать. Так как коты не обладают способностью к полету, данное множество оказывается пустым.
- Множество всех простых чисел, больших 100 и меньших 99. Нет простых чисел, которые одновременно больше 100 и меньше 99, поэтому данное множество также пусто.
- Множество всех динозавров, живущих в настоящее время. Динозавры вымерли миллионы лет назад, поэтому данное множество не содержит элементов.
Пустые множества являются важными концепциями в математике и используются для различных целей, в том числе в теории вероятностей и логике.
Пустое множество также играет роль в определении подмножества, так как любое множество является подмножеством пустого множества.
Важно отметить, что пустое множество не равно нулю. Оно представляет собой концепцию отсутствия элементов в множестве.