Движение материальной точки по окружности является одним из основных объектов изучения в физике и математике. Это неизменно привлекает внимание ученых и студентов, ведь окружность является одной из самых простых и понятных геометрических форм. Тем не менее, расчет пути движения точки по окружности может представлять определенные сложности и требовать применения специальных методов. В этой статье мы рассмотрим основные методы расчета пути движения и раскроем некоторые интересные секреты этого процесса.
Одним из наиболее простых и распространенных методов расчета пути движения материальной точки по окружности является применение геометрических и тригонометрических свойств окружности. Изучая эти свойства, мы можем легко определить радиус окружности и угол, на который смещается точка. Также мы можем определить длину дуги, пройденной точкой, и время, необходимое для ее преодоления.
Существуют и другие методы расчета пути движения материальной точки по окружности. Например, аналитический метод основан на использовании уравнений движения и дифференциальных уравнений. Этот метод требует более глубоких знаний в области математики и физики, но позволяет более точно определить путь движения и его параметры. Кроме того, существуют исключительные случаи, когда путь движения по окружности может быть более сложным и интересным, например, при наличии внешних воздействий или изменчивости радиуса окружности.
Путь движения материальной точки по окружности
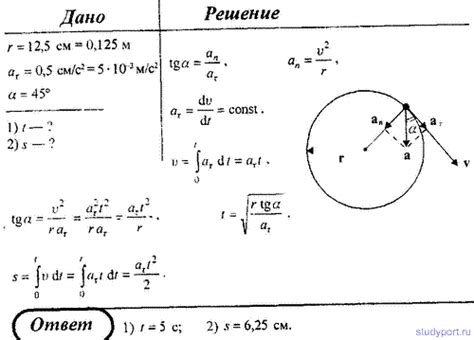
Основные характеристики движения материальной точки по окружности включают радиус окружности, скорость и ускорение точки, а также время, затраченное на один полный оборот вокруг окружности. Рассматривая данные характеристики, можно предсказать и анализировать движение точки и прогнозировать ее положение в любой момент времени.
Существует несколько методов расчета пути движения материальной точки по окружности. Один из них основан на использовании радиуса окружности и угла, на котором находится точка. Используя тригонометрические функции синуса и косинуса, можно определить координаты точки на окружности в зависимости от ее угла.
Другой распространенный метод расчета пути движения точки по окружности связан с использованием линейной скорости точки и времени. Линейная скорость точки равна ее скорости поделенной на радиус окружности. Это позволяет определить, какое расстояние пройдет точка за определенное время.
Изучение движения материальной точки по окружности важно во многих областях науки и техники, таких как физика, механика, астрономия и строительство. Понимание методов расчета и анализа пути движения точки по окружности помогает предсказывать движение объектов и разрабатывать эффективные системы и технологии.
Определение и свойства окружности

У окружности есть несколько важных свойств:
1. Центр окружности - это точка, от которой равны все расстояния до точек окружности.
2. Радиус окружности - это расстояние от центра окружности до любой точки на окружности. Все радиусы окружности равны друг другу.
3. Диаметр окружности - это отрезок, соединяющий две точки на окружности, и проходящий через ее центр. Диаметр равен удвоенному радиусу.
4. Окружность делит плоскость на две части: внутреннюю и внешнюю. Внутренняя часть называется кругом, ограниченным окружностью.
5. Окружность уникальна по тому, что она имеет постоянную длину окружности, независимо от ее радиуса. Длина окружности находится по формуле L = 2πr, где L - длина окружности, а r - радиус окружности. Здесь π (пи) - математическая константа, примерное значение которой равно 3,14159.
6. Вычисление площади круга осуществляется по формуле S = πr², где S - площадь круга, а r - радиус окружности.
Знание определения и свойств окружности важно для понимания пути движения материальной точки по окружности и методов расчета, связанных с данной темой.
Основные методы расчета пути движения
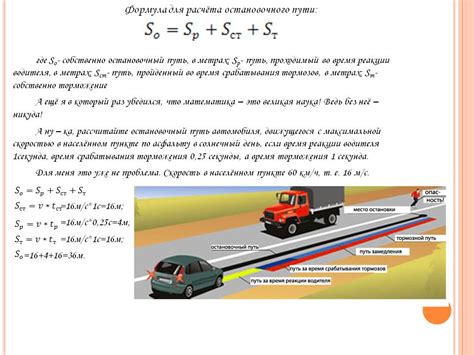
1. Геометрический метод:
Данный метод основывается на использовании геометрических свойств окружности и позволяет точно определить положение точки на траектории в любой момент времени. Для этого необходимо знать радиус окружности и угол поворота точки относительно начальной точки.
2. Кинематический метод:
Кинематический метод используется для определения скорости и ускорения точки на окружности в различные моменты времени. Для расчета пути движения необходимо знать начальную скорость и ускорение, радиус окружности и угловую скорость изменения положения точки.
3. Динамический метод:
Динамический метод позволяет учесть влияние сил, действующих на точку на окружности. Он основан на принципах классической механики и включает в себя расчет силы, момента силы и уравнений движения. Данный метод позволяет предсказать поведение точки в условиях внешних воздействий и определить ее путь движения.
Выбор метода расчета пути движения материальной точки по окружности зависит от поставленной задачи и доступной информации о системе. Каждый из методов имеет свои преимущества и ограничения, поэтому необходимо выбирать наиболее подходящий способ для конкретной ситуации.
Геометрический подход к расчету пути движения
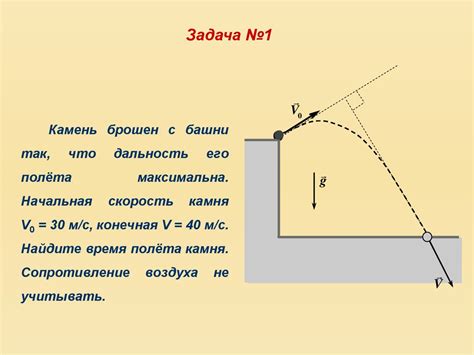
Расчет пути движения материальной точки по окружности может быть осуществлен с использованием геометрического подхода. Для этого необходимо учесть некоторые геометрические свойства окружности.
Первым шагом является определение радиуса окружности, который обозначается символом R. Радиус - это расстояние от центра окружности до любой точки на ее окружности. Значение радиуса может быть известно из условий задачи или вычислено исходя из других данных.
Далее необходимо определить длину окружности, которая выражается формулой:
L = 2πR,
где L - длина окружности, а π - это математическая константа, примерное значение которой равно 3,14159.
По длине окружности можно вычислить количество полных оборотов, которое пройдет точка за время движения. Для этого необходимо разделить длину пути на длину окружности:
n = S/L,
где n - количество полных оборотов, а S - длина пути движения.
Так как материальная точка движется по окружности, ее путь представляет собой дугу окружности. Длина дуги выражается формулой:
S = 2πRn,
где R - радиус окружности, n - количество полных оборотов, а S - длина пути движения.
Таким образом, геометрический подход к расчету пути движения материальной точки по окружности позволяет определить радиус окружности, длину окружности, количество полных оборотов и длину пути движения с использованием геометрических свойств окружности.
Теоретический подход к расчету пути движения

Исходя из геометрических свойств окружности, важно помнить, что радиус окружности – расстояние от центра до любой точки на окружности. Это свойство позволяет производить вычисления по положению точки относительно центра окружности.
Другой важный аспект – угол поворота, который определяет положение точки на окружности относительно начальной точки. Угол измеряется в радианах и может быть рассчитан с использованием тригонометрических функций, таких как синус и косинус.
Кроме того, для расчета пути движения необходимо учитывать скорость и время перемещения точки по окружности. Скорость в данном случае может быть выражена как отношение пути к времени, а время должно быть измерено в единицах времени, например, секундах или минутах.
После того как все необходимые параметры определены, можно приступить к расчету пути движения материальной точки по окружности с использованием соответствующих математических формул и уравнений.
Таким образом, теоретический подход к расчету пути движения материальной точки по окружности основывается на применении геометрических свойств окружности, использовании тригонометрических функций для определения угла поворота и учете скорости и времени для расчета пути.
Влияние физических параметров на путь движения
Путь движения материальной точки по окружности может быть существенно изменен в зависимости от изменения физических параметров, таких как масса, скорость, ускорение и радиус окружности.
Масса материальной точки влияет на ее инерцию и способность изменять направление движения. Чем больше масса, тем сильнее сила инерции, и точка будет более устойчива к изменениям траектории движения.
Скорость материальной точки также играет важную роль. Чем выше скорость, тем больше сила инерции и тем труднее изменить направление движения. Большая скорость может привести к изменению радиуса окружности и более крутому повороту.
Ускорение определяет изменение скорости точки со временем. Большое ускорение может привести к более сложному и изогнутому пути движения, в то время как малое ускорение может создать более прямую траекторию.
Радиус окружности является определяющим фактором для пути движения. Чем больше радиус, тем более плавный и округлый будет путь. Меньший радиус приведет к более крутому и изогнутому пути.
Итак, физические параметры, такие как масса, скорость, ускорение и радиус окружности, играют важную роль в определении пути движения материальной точки по окружности. Изменение этих параметров может значительно изменить траекторию движения и создать более сложные или более прямые пути.
Секреты точного расчета пути движения
1. Выбор подходящей модели
Правильный выбор подходящей модели для расчета пути движения на окружности является ключевым моментом. Существует несколько моделей, таких как модель гармонического движения и модель равномерного движения. Каждая из этих моделей имеет свои особенности и применяется в зависимости от конкретной задачи.
2. Учет всех факторов
Для точного расчета пути движения следует учесть все факторы, которые могут повлиять на результат. Это могут быть силы трения, сопротивления воздуха, внешние воздействия и другие факторы. Их учет позволит получить более реалистичные значения и точные результаты.
3. Использование математических формул
Для расчета пути движения на окружности можно использовать различные математические формулы. Например, можно применить формулы для вычисления радиуса окружности, периметра, углового перемещения и т. д. Использование математических формул позволяет получить точные значения и избежать ошибок в расчетах.
4. Работа с точными данными
Для достижения точности в расчетах следует работать с точными данными. При измерении параметров окружности следует использовать точные инструменты и методы измерений. Также стоит учитывать все поправки и погрешности, которые могут возникнуть при работе с данными.
В целом, точный расчет пути движения материальной точки по окружности требует внимания к деталям и учета всех факторов, которые могут повлиять на результаты расчетов. Правильное применение моделей, использование математических формул и работа с точными данными помогут получить более точные и достоверные результаты.