Пятиугольник – это одна из наиболее интересных и уникальных фигур в геометрии. В отличие от треугольника или четырехугольника, пятиугольник обладает некоторыми особенностями, которые делают его особенно значимым и привлекательным для изучения.
Одной из главных особенностей пятиугольника является его форма. У этой фигуры пять сторон и пять углов, что делает его более сложным и разнообразным с точки зрения свойств и связей между сторонами и углами. Более того, у пятиугольника есть что-то особенное, что отличает его от других многоугольников – это его уникальный центр симметрии.
Центр симметрии пятиугольника – это точка, которая делит фигуру на две равные и симметричные части относительно этой точки. Понятие симметрии играет важную роль в геометрии и имеет много применений в различных областях науки и искусства. В случае пятиугольника центр симметрии может располагаться внутри фигуры или на одной из его сторон.
Пятиугольник: каковы его особенности?

Вот некоторые интересные особенности пятиугольников:
| Углы: | Сумма всех углов пятиугольника всегда равна 540 градусам. |
| Стороны: | Все стороны пятиугольника могут быть разной длины или одинаковой длины. |
| Диагонали: | Пятиугольник имеет пять диагоналей – линии, соединяющие любые две вершины. |
| Центр симметрии: | Пятиугольник не имеет центра симметрии – линию или точку, которая разделяет фигуру на две равные части. |
| Площадь: | Площадь пятиугольника можно вычислить разными способами, в зависимости от известных данных о фигуре. |
В искусстве и архитектуре пятиугольники часто используются для создания эстетически приятных и симметричных композиций. Их уникальные особенности делают их интересными объектами изучения для математиков и любителей геометрии.
Форма и структура пятиугольника
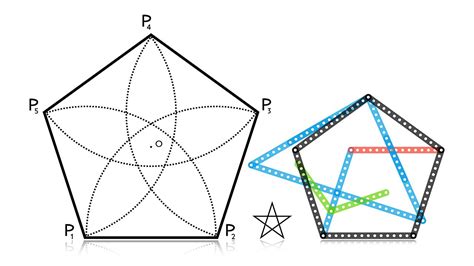
Все стороны пятиугольника могут быть разной длины и разным углом наклона, однако все пять углов пятиугольника всегда суммируются в 540 градусов. Это свойство позволяет определить, что сумма внутренних углов пятиугольника всегда будет постоянной и неизменной вне зависимости от размеров его сторон.
Структура пятиугольника также может быть важной характеристикой при его исследовании. Например, пятиугольник может быть выпуклым или невыпуклым. Выпуклый пятиугольник имеет все углы, направленные вовнутрь, что делает его «выпуклым» или «вогнутым» внутрь. Невыпуклый пятиугольник, наоборот, имеет углы, направленные внутрь, что делает его «невыпуклым» или «впуклым» внутрь.
Пятиугольник также может иметь различные типы симметрии, включая осевую симметрию и симметрию относительно центра. Осевая симметрия означает, что пятиугольник может быть разделен на две равные части путем отражения относительно некоторой оси. Центральная симметрия означает, что каждая точка пятиугольника имеет свою пару симметричных точек относительно центра пятиугольника.
Свойства и особенности пятиугольника
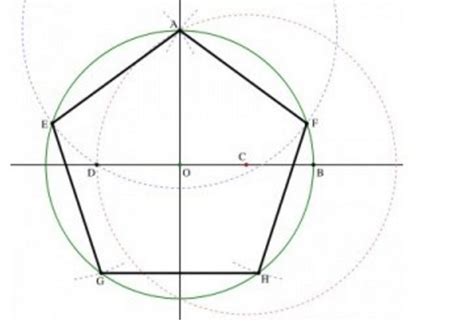
1. Углы пятиугольника:
Все углы пятиугольника меньше 180 градусов. Сумма всех углов пятиугольника всегда равна 540 градусов. Внутренние углы пятиугольника могут быть как остроугольными, так и тупоугольными.
2. Стороны пятиугольника:
У пятиугольника пять сторон, которые могут быть разной длины. Стороны пятиугольника могут быть одинаковой или разной длины.
3. Центр симметрии:
Пятиугольник имеет центр симметрии. Это значит, что если провести линию, соединяющую центр пятиугольника с любой его вершиной, то она будет делиться пополам и будет являться осью симметрии.
4. Площадь пятиугольника:
Площадь пятиугольника можно найти, разбивая его на треугольники и находя площади каждого из них. Формула для вычисления площади пятиугольника зависит от длин сторон и углов фигуры.
5. Периметр пятиугольника:
Периметр пятиугольника найдется суммированием длин всех его сторон. Формула периметра пятиугольника проста: P = a + b + c + d + e, где a, b, c, d и e - длины сторон пятиугольника.
Пятиугольник имеет много интересных свойств и особенностей, которые могут быть полезными при решении различных задач в геометрии и математике.
Центр симметрии пятиугольника

Для определения центра симметрии пятиугольника можно провести диагонали, соединяющие его вершины.
Центр симметрии пятиугольника является пересечением этих диагоналей. Если провести прямую через эту точку и центр пятиугольника, то она будет являться осью симметрии.
Центр симметрии пятиугольника имеет несколько важных свойств:
- Он равноудален от всех вершин пятиугольника.
- Он является точкой пересечения диагоналей пятиугольника.
- Он является точкой отражения каждой вершины пятиугольника относительно оси симметрии.
Центр симметрии пятиугольника отражает особенности геометрической структуры этой фигуры. Он играет важную роль в изучении и анализе пятиугольников и используется во многих областях науки и искусства.