Маткад - компьютерная программа, широко используемая в научных и инженерных расчетах, включающая в себя множество математических функций и операций. Одной из основных возможностей Маткада является вычисление корней уравнений различных типов. Возможность нахождения корней уравнений является очень важной для многих областей науки и техники.
Root - функция в Маткаде, предназначенная для решения уравнений. Она позволяет найти все корни уравнения или ограничиться только одним из них. Функция Root может использоваться для решения полиномиальных уравнений, трансцендентных уравнений, систем уравнений и т.д. Ее синтаксис достаточно прост: Root(уравнение, переменная).
Основной пример использования функции Root - решение квадратного уравнения. Например, чтобы найти корни уравнения x^2 - 5x + 6 = 0, можно использовать следующий код: Root(x^2 - 5x + 6 = 0, x). После выполнения этой команды Маткад найдет и выведет значения x, являющиеся корнями уравнения. В данном случае будет найдено два корня: x = 2 и x = 3.
Кроме того, функция Root позволяет находить комплексные корни уравнений. Например, чтобы найти все корни уравнения x^4 + 1 = 0, можно использовать следующий код: Root(x^4 + 1 = 0, x). Маткад найдет и выведет комплексные корни уравнения, такие как x = i и x = -i, где i - мнимая единица.
Что такое Root в Маткаде
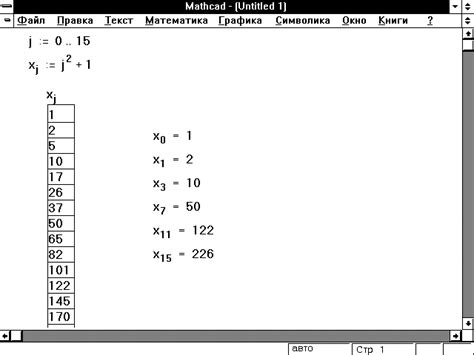
Root в Маткаде используется для решения различных математических задач, связанных с нахождением корней уравнений. Он позволяет найти корни как аналитически, так и численно.
Root в Маткаде имеет несколько вариантов использования. Основной синтаксис функции Root выглядит следующим образом:
- Root(Уравнение, переменная)
Здесь "Уравнение" – это математическое выражение, в котором содержится одно или несколько уравнений, а "переменная" – это переменная, корни которой необходимо найти. Результатом работы функции Root является список значений переменной, которые являются корнями заданного уравнения или системы уравнений.
Root позволяет найти не только численные значения корней, но и аналитическое представление решения. Если результатом работы функции будет аналитическая формула, то Маткад будет отображать ее в виде символьного выражения.
Также Root в Маткаде может применяться для поиска комплексных корней уравнений. Для этого нужно указать в качестве переменной комплексную переменную, например, i или j.
Использование функции Root в Маткаде значительно упрощает решение математических задач, связанных с поиском корней уравнений или систем уравнений. Это мощный инструмент для всех, кто работает в области математики, физики, инженерии и других наук.
Примеры использования Root в Маткаде

Вот несколько примеров использования функции Root:
Найти корни квадратного уравнения:
equation := x^2 + 2*x + 1 = 0; roots := Root(equation, x);В данном примере функция Root будет использована для нахождения корней квадратного уравнения x^2 + 2*x + 1 = 0.
Решить систему нелинейных уравнений:
equations := { x^2 + y^2 = 25, x + y = 7 }; solutions := Root(equations, {x, y});В этом примере функция Root будет использована для нахождения значений x и y, которые удовлетворяют системе уравнений x^2 + y^2 = 25 и x + y = 7.
Найти корни трансцендентного уравнения:
equation := sin(x) + 2*cos(x) = 0; roots := Root(equation, x);В этом примере функция Root будет использована для нахождения корней трансцендентного уравнения sin(x) + 2*cos(x) = 0.
Root является мощным инструментом, который может использоваться для аналитического решения различных типов уравнений. Благодаря ему, можно находить точные значения корней и решать сложные задачи.
Технические особенности Root в Маткаде
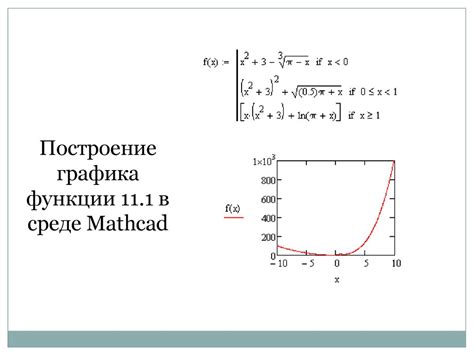
Во-первых, функция Root в Маткаде может решать не только алгебраические уравнения, но и трансцендентные. Это означает, что она способна находить корни не только для простых полиномиальных уравнений, но и для более сложных функций, включающих, например, экспоненциальные и тригонометрические компоненты.
Во-вторых, функция Root возвращает действительные и комплексные корни уравнения. При этом она обладает некоторой встроенной надежностью в определении типа корней - функция автоматически определит, являются ли они действительными или комплексными. Однако, это может привести к ошибкам при работе с функцией в случае, если она не смогла правильно определить тип корней.
В-третьих, функция Root может иметь несколько различных синтаксисов, что позволяет более гибко определять уравнения, для которых нужно найти корни. Это включает в себя возможность указания начальных приближений для поиска корней, задание области нахождения корней и другие дополнительные параметры.
Изучение и использование функции Root в Маткаде требует некоторого опыта и понимания особенностей ее работы. Однако, благодаря своей мощности и гибкости, эта функция является незаменимым инструментом в решении различных математических задач.
Root в Маткаде и его применение в инженерных расчетах
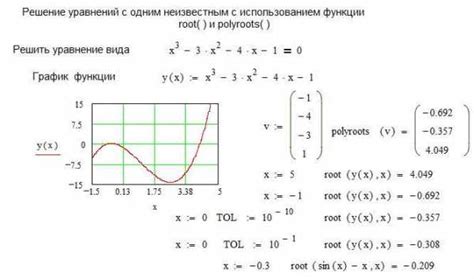
Применение root в инженерных расчетах может быть разнообразным. Например, основываясь на уравнениях движения и физических законах, можно использовать root для нахождения корней и определения значений важных параметров, таких как время, скорость, ускорение и многое другое.
Root в Маткаде также может быть использован для решения уравнений, связанных с электрическими цепями, механикой материалов, гидравликой и другими инженерными дисциплинами. При работе с большим количеством данных и сложных математических моделей, использование root значительно упрощает и ускоряет расчеты.
Одним из преимуществ использования root в Маткаде является возможность решения нелинейных уравнений, которые не могут быть решены аналитически. Вместо этого, Маткад использует численные методы для приближенного нахождения корней. Это особенно полезно при моделировании сложных систем и анализе данных с неизвестными параметрами.