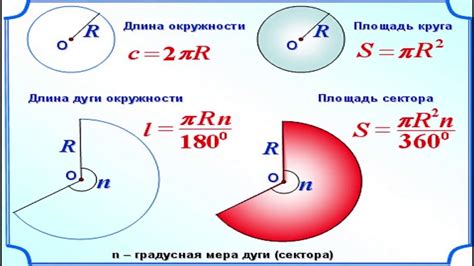
Окружность - одна из основных геометрических фигур, состоящая из всех точек плоскости, равноудаленных от заданной точки, называемой центром окружности. Она имеет множество интересных свойств и является объектом исследования в различных областях науки и инженерии.
Длина окружности - это периметр окружности, то есть длина замкнутой кривой, которая составляет окружность. Расчет длины окружности является важной задачей в геометрии и имеет широкое применение в различных областях, таких как строительство, архитектура, физика и математика.
Интересно, что длина окружности можно выразить через ее площадь. Формула для расчета длины окружности с заданной площадью S выглядит следующим образом:
L = 2π√(S/π)
где L - длина окружности, S - площадь, π - математическая константа, приближенно равная 3,14159.
Что такое окружность и площадь?
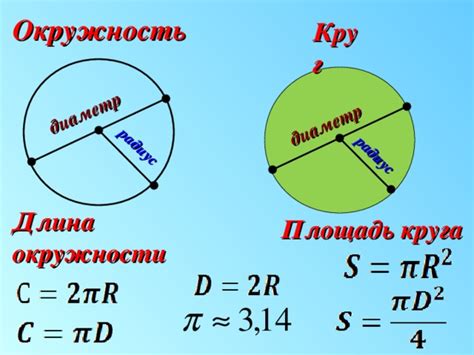
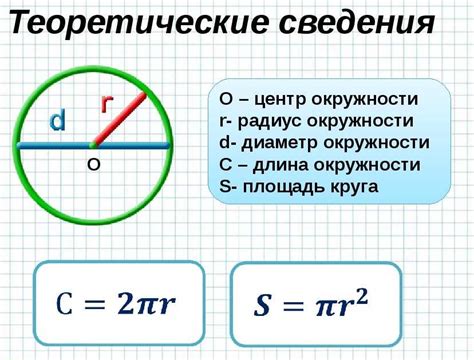
Радиус - это расстояние от центра окружности до любой точки на ее окружности. Диаметр - это отрезок, соединяющий две противоположные точки на окружности и проходящий через ее центр. Длина окружности равна произведению диаметра на число пи (π).
Площадь - это мера поверхности, занимаемой фигурой на плоскости. Для окружности площадь определяется как произведение квадрата радиуса на число пи.
Так, для окружности с площадью 4π, длину окружности можно найти, зная ее площадь. Для этого нужно сначала найти радиус окружности, а затем умножить его на 2π (2πr).
Итак, окружность и площадь - основные понятия геометрии, которые позволяют описывать и анализировать формы и размеры фигур на плоскости. Знание этих понятий позволяет нам решать разнообразные задачи и применять их в реальной жизни.
Как связаны площадь и длина окружности?
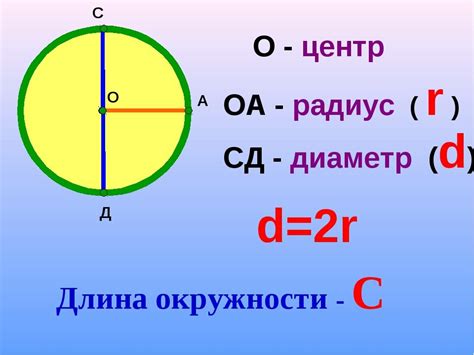
Длина окружности, с другой стороны, является мерой длины или периметра окружности. Она измеряется в единицах длины, например, метрах, сантиметрах или дюймах.
Удивительным образом, площадь и длина окружности тесно связаны друг с другом. Для окружности заданного радиуса, существует простая формула, которая объединяет эти две характеристики: S = π * r^2 и C = 2 * π * r, где S - площадь, C - длина окружности, а r - радиус окружности.
Исходя из этих формул, мы можем сказать, что площадь окружности пропорциональна квадрату радиуса, тогда как длина окружности пропорциональна самому радиусу. Это значит, что увеличение радиуса будет приводить к росту и площади, и длины окружности. Также следует отметить, что пропорциональность между длиной и площадью окружности относится только к окружностям одинакового радиуса.
Понимая связь между площадью и длиной окружности, мы можем использовать эти характеристики для решения различных задач и проблем, связанных с окружностями, в таких областях, как геометрия, физика и инженерия.
Формула расчета площади окружности
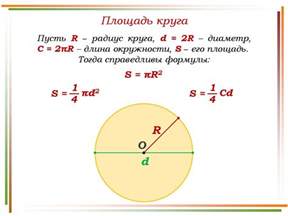
Формула для расчета площади окружности представляет собой простое математическое выражение. Она основана на радиусе окружности, который обозначается символом R. Формула выглядит следующим образом: S = π * R^2.
В данной формуле π (пи) – это математическая константа, которая приближенно равна 3,1415926535. Она является важнейшим числовым значением, необходимым для выполнения расчетов связанных с окружностью. Радиус R – это расстояние от центра окружности до ее окружности.
Используя данную формулу, можно рассчитать площадь окружности по известному радиусу. Для этого нужно возвести радиус в квадрат и умножить его на число π. Полученная площадь будет выражена в квадратных единицах при условии, что радиус измеряется в одних и тех же единицах длины.
Формула расчета площади окружности позволяет быстро и точно определить площадь этой геометрической фигуры. Она проста в использовании и находит широкое применение в различных областях, таких как строительство, геодезия, физика и другие.
Как найти радиус окружности?
Радиус = √(Площадь окружности / Пи)
В данном случае, площадь окружности равна 4п, поэтому формулу можно записать как:
Радиус = √(4п / Пи)
Используя значения чисел, получим:
| Радиус = √(4п / Пи) | Радиус = √(4 / 1) | Радиус = 2 |
Таким образом, радиус окружности с площадью 4п равен 2.
Как найти площадь окружности?
Чтобы найти площадь окружности, необходимо знать ее радиус. Радиус - это расстояние от центра окружности до любой точки на ее окружности. Для расчета площади окружности нужно возвести радиус в квадрат и умножить на число пи.
| Шаг | Формула | Пример |
|---|---|---|
| 1 | Найти радиус окружности (r) | r = 2 см |
| 2 | Возвести радиус в квадрат (r^2) | r^2 = 4 см^2 |
| 3 | Умножить результат на число пи (π) | S = π * 4 см^2 = 4π см^2 |
Таким образом, площадь окружности с радиусом 2 см равна 4π квадратных сантиметров.
Формула расчета длины окружности
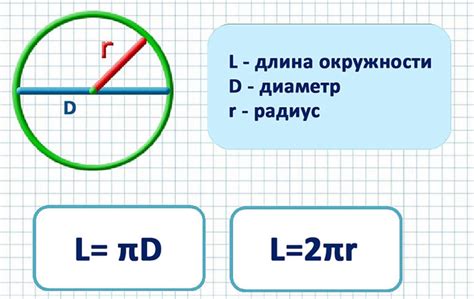
L = 2πr
где L - длина окружности, π - математическая константа, приближенно равная 3,14159, а r - радиус окружности.
Таким образом, чтобы найти длину окружности, необходимо умножить радиус на два и на математическую константу π. Например, при известном значении площади окружности, равной 4π, длина окружности будет равна 4.
Как найти длину окружности по радиусу?
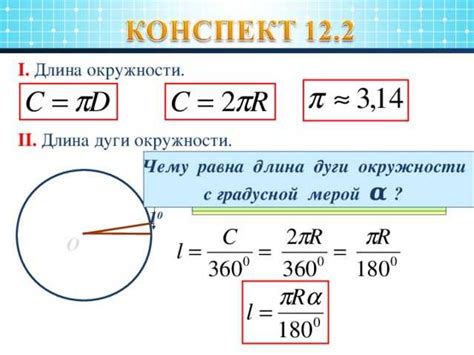
Формула для расчета длины окружности - это P = 2πr, где P - длина окружности, а r - радиус окружности. Число π (пи) примерно равно 3,14159 или можно использовать его приближенное значение 3,14.
Для того чтобы найти длину окружности по радиусу, нужно умножить радиус на 2π. Например, если радиус окружности равен 5, то длина окружности будет равна 2 * 3,14 * 5 = 31,4.
Таким образом, для расчета длины окружности по радиусу необходимо использовать формулу P = 2πr, где P - длина окружности, а r - радиус окружности.
Как найти длину окружности по диаметру?
Длина окружности = π * диаметр
Здесь π (пи) - это математическая постоянная, которая приближенно равна 3.14 или 22/7. Диаметр - это расстояние между двумя точками, находящимися на противоположных концах окружности и проходящими через ее центр.
Итак, чтобы найти длину окружности по диаметру, нужно умножить диаметр на π. Например, если диаметр равен 10 единицам, то длина окружности будет:
Длина окружности = 3.14 * 10 = 31.4 единицы
Таким образом, вы можете легко найти длину окружности, если известен ее диаметр, используя простую формулу. Это поможет вам в решении различных задач, связанных с геометрией и окружностями.