Один из основных элементов геометрии – нахождение углов между прямыми. Для решения подобных задач используются различные формулы и методы. Один из наиболее важных параметров при решении таких задач – синус угла между прямыми. От знания этого параметра зависит понимание угловых отношений в пространстве и возможность решения подобных задач с высокой точностью.
Синус угла между прямыми является математическим понятием, которое определяет взаимное положение двух прямых в пространстве. Для его расчета существует специальная формула, которая позволяет найти значение синуса угла между прямыми на основе известных данных о направляющих векторах этих прямых.
Формула для расчета синуса угла между прямыми выглядит следующим образом:
sin(α) = |(A1*B2 - A2*B1)| / (sqrt(A1^2 + B1^2) * sqrt(A2^2 + B2^2))
где A1, B1 и A2, B2 – коэффициенты направляющих векторов прямых.
Для лучшего понимания приведенной формулы и ее использования, рассмотрим несколько практических примеров нахождения синуса угла между прямыми для различных начальных данных.
Определение синуса угла между прямыми
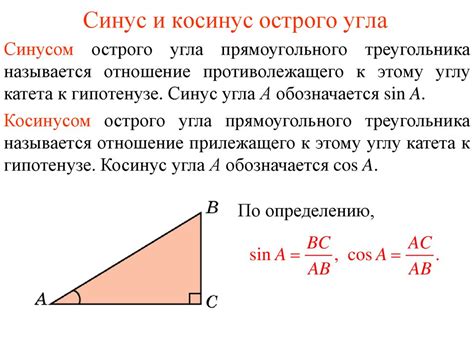
Для расчета синуса угла между прямыми существует специальная формула, которая основана на знании коэффициентов уравнений этих прямых. Пусть первая прямая задается уравнением a1x + b1y + c1 = 0, а вторая прямая - уравнением a2x + b2y + c2 = 0.
Синус угла между прямыми определяется следующей формулой:
Где a1 и b1 - коэффициенты первого уравнения прямой, a2 и b2 - коэффициенты второго уравнения прямой.
С помощью данной формулы можно точно определить синус угла между данными прямыми и применить его в различных задачах и расчетах.
Формула для расчета синуса угла между прямыми
Синус угла между двумя прямыми может быть найден с использованием формулы:
| Формула | Описание | Примечание |
|---|---|---|
| \( \sin(\theta) = \fraca_1b_2 - a_2b_1}{{\sqrt{{a_1^2 + a_2^2}} \cdot \sqrt{{b_1^2 + b_2^2}}}} \) | Формула для расчета синуса угла между прямыми, заданными уравнениями \(a_1x + a_2y + a_3 = 0\) и \(b_1x + b_2y + b_3 = 0\) | Угол \(\theta\) должен быть в радианах |
В этой формуле \( a_1, a_2, a_3\) - коэффициенты уравнения первой прямой, а \( b_1, b_2, b_3\) - коэффициенты уравнения второй прямой.
Для использования этой формулы, необходимо знать коэффициенты уравнений обоих прямых. Подставляя их значения в формулу, мы можем вычислить синус угла между этими прямыми.
Важно отметить, что угол, полученный с использованием этой формулы, будет в радианах. Для перевода угла из радианов в градусы можно использовать формулу \( \text{градусы} = \text{радианы} \times \frac{{180}}{\pi} \).
Пример расчета синуса угла между прямыми
Представим, что у нас есть две прямые: l1 и l2. Известны их уравнения:
- l1: 3x + 2y = 5
- l2: -2x + 5y = 7
Для вычисления синуса угла между этими прямыми необходимо знать их направляющие векторы. Найдем их по следующим формулам:
- Направляющий вектор l1: (3, 2)
- Направляющий вектор l2: (-2, 5)
Затем найдем скалярное произведение этих векторов и модули их длин:
- Скалярное произведение: (3 * -2) + (2 * 5) = -6 + 10 = 4
- Модуль длины вектора l1: sqrt((3^2) + (2^2)) = sqrt(9 + 4) = sqrt(13)
- Модуль длины вектора l2: sqrt(((-2)^2) + (5^2)) = sqrt(4 + 25) = sqrt(29)
Теперь, применив формулу для вычисления синуса угла между прямыми:
- sin(α) = |(3, 2) * (-2, 5)| / (sqrt(13) * sqrt(29)) = |4| / (sqrt(13) * sqrt(29)) ≈ 0.286
Получаем, что синус угла между прямыми l1 и l2 ≈ 0.286.
Этот пример показывает, как можно вычислить синус угла между прямыми, используя их уравнения и направляющие векторы. Такой расчет может быть полезен, например, при решении задач геометрии или физики.
Практические примеры нахождения синуса угла между прямыми
Пример 1:
Даны следующие уравнения прямых:
l1: 2x + 3y - 4 = 0
l2: 3x - 4y + 5 = 0
Сначала найдем угол между прямыми по формуле:
sin(θ) = |a1·a2| / (|a1| · |a2|)
Где a1 и a2 - векторы нормальных (коэффициенты перед x и y) этих прямых.
Подставим значения коэффициентов из уравнений прямых в формулу:
sin(θ) = |2·3 + 3·(-4)| / (sqrt(22 + 32) · sqrt(32 + (-4)2))
sin(θ) = |-6 + (-12)| / (sqrt(4 + 9) · sqrt(9 + 16))
sin(θ) = |-18| / (sqrt(13) · sqrt(25))
sin(θ) = 18 / (sqrt(13) · 5)
Значение синуса угла между прямыми составляет 18 / (sqrt(13) · 5).
Пример 2:
Даны уравнения прямых:
l1: y = 2x + 1
l2: y = -3x - 5
Перепишем уравнения в общем виде, чтобы были видны коэффициенты:
l1: 2x - y + 1 = 0
l2: 3x + y + 5 = 0
Теперь применим формулу:
sin(θ) = |a1·a2| / (|a1| · |a2|)
Подставим значения коэффициентов из уравнений прямых:
sin(θ) = |2·3 + (-1)·1| / (sqrt(22 + (-1)2) · sqrt(32 + 12))
sin(θ) = |6 - 1| / (sqrt(4 + 1) · sqrt(9 + 1))
sin(θ) = |5| / (sqrt(5) · sqrt(10))
sin(θ) = 5 / (sqrt(5) · sqrt(10))
Значение синуса угла между прямыми составляет 5 / (sqrt(5) · sqrt(10)).
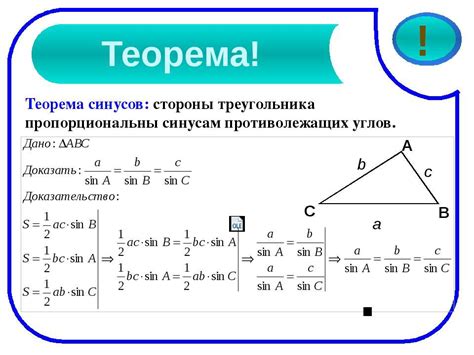
Таким образом, расчет синуса угла между прямыми позволяет определить степень их взаимной пересекаемости или параллельности.