Геометрия - одна из старейших наук, изучающая пространственные фигуры и их свойства. Один из важных аспектов, с которыми сталкиваются геометры, - это отношение длины сторон различных геометрических фигур. Отношение длины сторон позволяет нам понять, насколько стороны фигур связаны друг с другом и как они соотносятся между собой. В этой статье мы рассмотрим основные формулы и принципы, которые помогут найти отношение длины сторон в геометрии.
В геометрии отношение длины сторон определяется с помощью соотношения между длинами двух сторон. Это соотношение может быть выражено в виде десятичной дроби, десятичной дроби с периодом или дроби. Например, отношение длины сторон треугольника может быть 1:2 или 0.5.
Отношение длины сторон в геометрии можно найти с помощью различных формул и принципов. В зависимости от типа фигуры, есть разные подходы к вычислению отношения длины сторон. Например, для треугольника существует формула, известная как "теорема Пифагора". Согласно этой формуле, квадрат длины гипотенузы равен сумме квадратов длин двух катетов. Это позволяет нам вычислить отношение длины гипотенузы к длине одного из катетов.
Основы геометрии: длины сторон
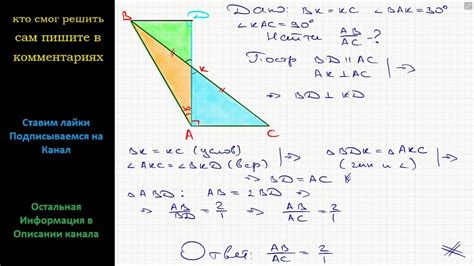
Длина стороны – это величина, равная расстоянию между двумя точками на геометрической фигуре. Для вычисления длины стороны достаточно знать координаты этих двух точек и применить соответствующую формулу.
В треугольнике, наиболее простой и распространенной геометрической фигуре, для вычисления длины сторон можно использовать теорему Пифагора. Согласно этой теореме, квадрат длины гипотенузы (стороны, противоположной прямому углу) в прямоугольном треугольнике равен сумме квадратов длин двух других сторон. Таким образом, зная длины двух сторон, можно найти длину третьей стороны посредством извлечения корня из разности квадратов длин сторон.
Кроме треугольника, длины сторон играют важную роль в других геометрических фигурах, таких как прямоугольник, квадрат, пятиугольник и многогранник. В каждом конкретном случае вычисление длин сторон осуществляется с использованием соответствующих формул и принципов.
Понимание длин сторон в геометрии позволяет проводить различные вычисления и устанавливать соотношения между сторонами геометрических фигур. Это является важным элементом при решении задач и построении сложных конструкций.
Таким образом, знание основ геометрии и умение вычислять длины сторон позволяет более точно изучать и анализировать геометрические объекты и их свойства.
Определение отношения длины сторон в геометрии
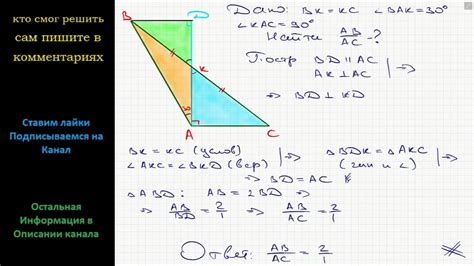
Отношение длины сторон может быть выражено численными значениями или в виде пропорции. Обычно оно записывается в виде a:b, где a и b представляют собой длины каждой из сторон фигуры.
В некоторых случаях отношение длины сторон может быть выражено с помощью формулы. Например, в треугольнике, отношение длины стороны косинусу соответствующего угла может быть определено с помощью теоремы косинусов.
Отношение длины сторон является важным инструментом для анализа и описания геометрических фигур. Оно позволяет установить связь между различными сторонами фигуры и использовать эту информацию для решения задач и нахождения дополнительных свойств фигуры.
Принципы нахождения отношения длин сторон

1. Принцип подобия треугольников: если два треугольника подобны, то отношение длин их сторон равно отношению соответствующих сторон. Например, если у двух треугольников соответствующие стороны имеют отношение 2:1, то можно утверждать, что данные треугольники подобны.
2. Принцип равных долей: если две фигуры содержат одинаковые или пропорциональные доли, то отношение длин их сторон будет соответствовать этим процентам. Например, если у двух прямоугольников одна сторона составляет 1/3 от общей площади фигуры, то отношение длины этой стороны к общей длине будет также составлять 1/3.
3. Принцип теоремы Пифагора: в прямоугольном треугольнике отношение длин катетов может быть вычислено с использованием теоремы Пифагора. Если катеты имеют длины a и b, а гипотенуза c, то отношение длин катетов равно a:b, а отношение длины гипотенузы к длине катета равно c:a или c:b.
| Фигура | Отношение длин сторон |
|---|---|
| Квадрат | 1:1 |
| Прямоугольник | пропорциональное отношение сторон |
| Треугольник | зависит от подобия треугольников |
| Круг | зависит от радиуса и диаметра |
Запомнив эти принципы, вы сможете легче определять отношение длин сторон в различных геометрических фигурах и использовать их для решения задач на геометрию.
Формулы для расчета отношения длин сторон
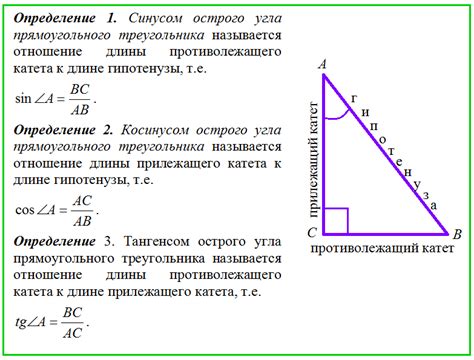
Отношение длин сторон в геометрии может быть очень полезным инструментом для решения различных задач. Существует несколько формул, которые позволяют найти отношение длин сторон в различных геометрических фигурах.
Для треугольника с заданными длинами сторон a, b и c можно использовать формулу:
a:b:c = dab:dbc:dac
где dab, dbc и dac - соответствующие расстояния между вершинами треугольника.
Для прямоугольного треугольника с катетами a и b и гипотенузой c отношение длин сторон можно найти с помощью следующей формулы:
a:b:c = a2:b2:c2
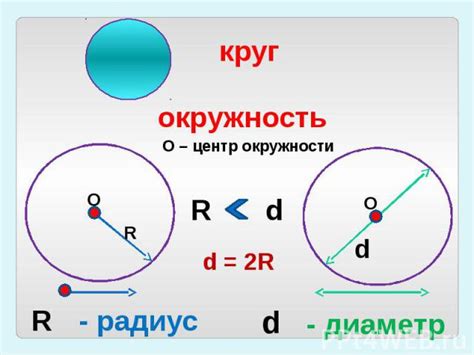
Если даны радиусы окружностей r1 и r2, то можно найти отношение их длин сторон по формуле:
r1:r2 = d1:d2
где d1 и d2 - диаметры соответствующих окружностей.
Формулы для расчета отношения длин сторон в геометрии могут быть очень полезными для решения различных задач. Используйте их для нахождения неизвестных значений и доказательства геометрических соотношений.
Важность отношения длин сторон в геометрии
В геометрии существуют различные фигуры, такие как треугольники, квадраты, прямоугольники и другие. Однако, не все фигуры имеют одинаковые свойства и формулы для вычислений. Отношение длин сторон позволяет определить, какие свойства и формулы относятся к данной фигуре.
Для примера, рассмотрим треугольники. У треугольника существуют три стороны - a, b и с. Если мы знаем отношение длин двух сторон треугольника, мы можем вывести формулы для нахождения третьей стороны и углов треугольника. Например, если мы знаем отношение длин сторон a и b, мы можем использовать теорему Пифагора для нахождения длины третьей стороны c.
Отношение длин сторон также имеет важное значение при изучении пропорциональности и подобных фигур. Если отношение длин сторон двух фигур равно, то эти фигуры считаются подобными. Это позволяет нам установить соответствия между сторонами и углами подобных фигур и использовать их для решения задач и вычислений.
Примеры применения отношения длин сторон

Отношение длин сторон в геометрии широко используется для решения различных задач. Рассмотрим несколько примеров применения этого понятия:
1. Подобные фигуры
Если две фигуры подобны, то соответствующие стороны этих фигур имеют одно и то же отношение.
Например, пусть у нас есть два треугольника АВС и DEF. Если треугольники подобны, то отношение длин сторон АВ к DE, BC к EF и AC к DF будет одинаковым.
2. Разделение отрезка в заданном отношении
Отношение длин сторон может быть использовано для разделения отрезка в заданном отношении. Например, пусть у нас есть отрезок AB, и мы хотим разделить его на две части в отношении 2:3. Для этого мы можем построить точку C на отрезке AB так, чтобы отношение AC к CB было равно 2:3.
3. Подсчет площадей фигур
Отношение длин сторон может быть также использовано для подсчета площадей фигур. Например, если у нас есть два прямоугольника, и один прямоугольник подобен другому с отношением длин сторон 1:2, то площадь большего прямоугольника будет в два раза больше площади меньшего прямоугольника.
Советы по нахождению и использованию отношения длин сторон в геометрии
Вот несколько советов по нахождению и использованию отношения длин сторон в геометрии:
| 1. Используйте соответствующие стороны подобных фигур. | Когда у вас есть две подобные фигуры, отношение длин сторон одной фигуры к длинам соответствующих сторон другой фигуры будет постоянным. Используйте это отношение, чтобы находить неизвестные значения. |
| 2. Примените теорему Пифагора. | Теорема Пифагора устанавливает связь между длинами сторон прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Используйте эту формулу, чтобы определить отношение длин сторон в прямоугольных треугольниках. |
| 3. Воспользуйтесь теоремой Талеса. | Теорема Талеса объясняет, как соотносятся длины отрезков, проведенных параллельно стороне треугольника. Используйте эту теорему, чтобы определить отношение длин сторон треугольника в различных ситуациях. |
| 4. Пользуйтесь свойствами сходных треугольников. | Сходные треугольники имеют пропорциональные стороны. Используйте это свойство, чтобы находить отношения длин сторон в сложных фигурах, состоящих из сходных треугольников. |
Зная эти советы, вы сможете лучше разобраться с отношениями длин сторон в геометрии. Помните, что отношение длин сторон может быть инструментом для решения различных задач и для выявления связей между элементами фигур.