Рассчитать периметр и площадь - одно из базовых заданий в математике, которое пригодится в повседневной жизни и при изучении различных дисциплин. Существует несколько способов расчета: от простого и быстрого, до более точного и сложного. В данной статье мы рассмотрим простой метод, который позволяет с легкостью найти периметр и площадь, а также точную формулу, которая подходит для более сложных случаев.
Простой метод расчета периметра и площади основан на использовании базовых знаний о геометрии и длинах сторон фигуры. Для этого необходимо знать форму фигуры и ее размеры. Например, для прямоугольника нужно знать длину и ширину, для круга - радиус, для треугольника - длины сторон и т.д. Далее, используя соответствующие формулы, можно вычислить периметр и площадь.
Точная формула для расчета периметра и площади может быть сложнее и включать в себя более сложные математические операции, но она позволяет получить более точные результаты. Например, для расчета площади треугольника можно использовать формулу Герона, которая требует знания длин всех его сторон. При этом результат будет точнее, чем при использовании простого метода.
Методы расчета периметра и площади: доступное решение и математическая формула

Доступное решение: одним из простых и доступных методов для расчета периметра и площади является использование формул для прямоугольника, квадрата, круга и других простых геометрических фигур. Например, для прямоугольника периметр равен сумме длин всех его сторон, а площадь - произведению длины и ширины.
Если у вас прямоугольник со сторонами a и b, то периметр равен P = 2 * (a + b), а площадь равна S = a * b.
Аналогично, для круга радиусом r, периметр равен P = 2 * π * r, а площадь равна S = π * r^2, где π примерно равно 3.14159.
Математическая формула: для более сложных фигур, таких как треугольник или многоугольник, существуют специальные математические формулы, которые позволяют точно рассчитать их периметр и площадь. Например, для равностороннего треугольника со стороной a, периметр равен P = 3 * a, а площадь равна S = (a^2 * √3) / 4.
В общем случае, для многоугольника можно использовать формулы Герона для расчета его площади и суммирование длин всех сторон для расчета периметра.
Используя соответствующие формулы для каждой геометрической фигуры, вы сможете рассчитать периметр и площадь с необходимой точностью.
Периметр и площадь: основные понятия и их значение в геометрии
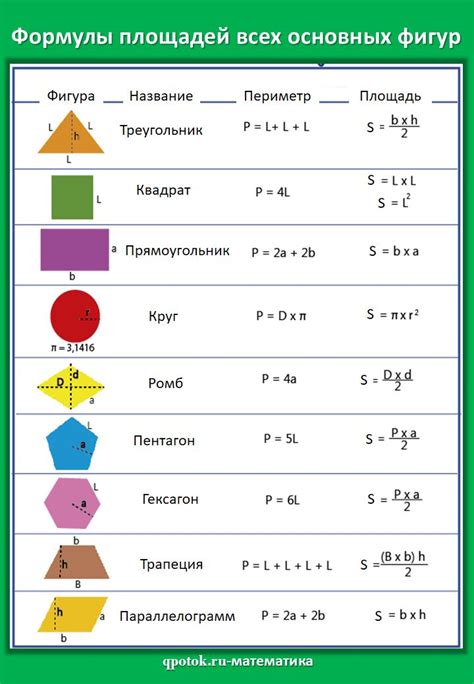
Периметр - это сумма длин всех сторон фигуры. Он позволяет определить длину окружности, границы многоугольника или длину периметра круга. Периметр выражается в линейных единицах измерения, таких как сантиметры, метры или футы, и позволяет оценивать длину или общий объем фигуры.
Площадь - это мера поверхности фигуры. Она определяет количество площади, занимаемой фигурой на плоскости или в пространстве. Площадь выражается в квадратных единицах измерения, таких как квадратные сантиметры, квадратные метры или квадратные футы. Площадь фигуры может быть использована для вычисления объема, количества материалов или растояния между объектами.
Зная периметр и площадь фигуры, мы можем решать различные задачи, связанные с геометрией. Например, мы можем определить оптимальный размер забора для ограждения участка, или вычислить количество краски, необходимое для покраски стен комнаты.
Периметр и площадь также используются в различных областях науки и инженерии, включая архитектуру, градостроительство, дизайн и технику. Они позволяют анализировать формы, оптимизировать конструкции и проводить точные расчеты. Понимание этих понятий является важным для успешного решения задач по геометрии и применения их в практической деятельности.
Простой метод расчета площади фигуры: принцип и шаги для выполнения

Принцип этого метода заключается в разбиении фигуры на более простые геометрические фигуры, площади которых легче вычислить. Затем, найденные значения площадей суммируются, и получается итоговая площадь фигуры.
Шаги для выполнения простого метода расчета площади фигуры:
- Выберите фигуру, площадь которой требуется вычислить.
- Проанализируйте фигуру и разбейте ее на более простые фигуры, площади которых вы знаете или можете легко вычислить.
- Вычислите площади каждой из простых фигур по известным формулам (например, площадь квадрата равна стороне в квадрате).
- Сложите найденные значения площадей простых фигур.
- Получите итоговую площадь фигуры.
Простой метод расчета площади фигуры особенно полезен, когда фигура имеет сложную форму, которую сложно описать единственной формулой. Используя этот метод, можно разбить сложную фигуру на несколько более простых, и вычислить их площади отдельно.
Таким образом, простой метод расчета площади фигуры позволяет упростить выполнение задачи, особенно в случае сложных фигур, и получить точный результат.
Определение периметра фигуры: простой и понятный метод

Периметр фигуры представляет собой сумму длин всех сторон этой фигуры. Для определения периметра можно использовать простые и понятные методы.
Если фигура – это прямоугольник, то периметр равен удвоенной сумме длин его сторон. Для определения периметра прямоугольника необходимо измерить длину двух смежных сторон и умножить каждую из них на 2, а затем сложить результаты.
Для фигуры, состоящей из прямоугольника и полукруга, чтобы найти периметр, нужно измерить длину прямоугольника и сумму длин двух сторон полукруга. Далее сложить все измеренные значения.
Если фигура является треугольником, то периметр равен сумме длин его трех сторон. Для определения периметра треугольника необходимо измерить длину каждой его стороны и сложить результаты.
Некоторые фигуры, например, круг, могут иметь бесконечное количество сторон. В таких случаях для определения периметра можно использовать точную формулу.
Периметр фигуры является важным показателем и может использоваться для определения ее размеров, а также для решения различных задач в геометрии.
Точная формула для расчета площади фигуры: как применить?
Точная формула для расчета площади фигуры предоставляет возможность получить наиболее точные результаты при определении площади различных геометрических форм. Этот метод особенно полезен, когда необходимо рассчитать площадь сложных или нетрадиционных фигур, для которых нет простых формул.
Применение точной формулы для расчета площади фигуры требует знания основных математических понятий и умения применять соответствующие формулы. Перед использованием точной формулы следует убедиться, что вы правильно определили все необходимые данные и измерения фигуры.
Одним из примеров точной формулы для расчета площади является формула Герона для расчета площади треугольника по его сторонам. Для применения этой формулы необходимо знать длины всех трех сторон треугольника.
Другим примером точной формулы является формула Пи для расчета площади круга. Данная формула основана на радиусе круга и позволяет рассчитать его площадь точно.
Если вы не уверены в точности своих измерений или имеете данные, которые подразумевают использование приближенных значений, не рекомендуется применять точную формулу. В таких случаях более простые методы, такие как радиус-мера или формула Герона, могут оказаться более практичными.
В итоге, точная формула для расчета площади фигуры предоставляет более точные результаты, но требует большей подготовки и усилий для правильного определения всех необходимых значений. При правильном применении точных формул можно получить наиболее точные результаты для расчета площади сложных геометрических форм.
Уравнения и переменные: как использовать формулу для расчета площади

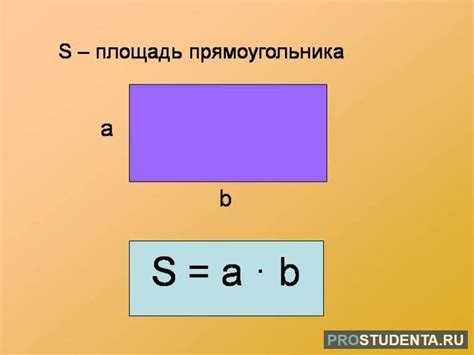
Когда речь идет о расчете площади, необходимо использовать формулу, которая позволяет найти точное значение. Для прямоугольников и квадратов площадь можно найти, умножив длину на ширину. Но что делать, если фигура имеет более сложную форму?
Для того чтобы найти площадь сложной фигуры, необходимо разбить ее на более простые части, для каждой из которых можно использовать известную формулу. Расчет площади фигуры будет представлять собой сумму площадей этих частей.
Для примера рассмотрим фигуру, состоящую из треугольника и прямоугольника. Найдем площадь каждой части и сложим их. Включим расчет в программу, используя переменные для хранения длин сторон.
Для прямоугольника зададим ширину (a) и длину (b). Площадь прямоугольника (S1) можно найти, используя формулу: S1 = a * b.
Для треугольника зададим основание (c) и высоту (h). Площадь треугольника (S2) можно найти, используя формулу: S2 = 0.5 * c * h.
Зная значения длин сторон и высоты, мы можем подставить их в уравнения и вычислить площади каждой части фигуры. Далее остается только сложить полученные площади, чтобы найти общую площадь фигуры.
Использование формулы и переменных при расчете площади позволяет нам получить точный результат, а также упрощает выполнение вычислений на компьютере.
Итак, уравнения и переменные - неотъемлемая часть расчета площади сложных фигур. Используя соответствующие формулы и значения переменных, вы сможете эффективно рассчитать площадь любой фигуры.
Расчет периметра фигуры: простой метод и его ограничения

Для многих простых фигур, таких как квадраты, прямоугольники и треугольники, расчет периметра может быть выполнен с помощью простых формул. Например, для прямоугольника периметр вычисляется по формуле:
Периметр прямоугольника = 2 * (длина + ширина)
Однако, для сложных и нестандартных фигур, таких как сегменты окружности или фигуры с изогнутыми сторонами, прямой расчет периметра может быть сложным и неточным. В таких случаях специалисты обычно используют более сложные методы, основанные на численных расчетах или аппроксимации.
Простая формула для расчета периметра имеет свои ограничения. Она предназначена только для определенных фигур и не способна обработать нестандартные или сложные случаи. Например, для неправильного многоугольника без правильных сторон и углов, простая формула может дать неточный результат.
Важно учитывать, что формулы для расчета периметра основываются на предположениях о геометрической форме фигуры. Если форма не совсем соответствует этим предположениям, результаты могут быть неточными или сильно искаженными.
Чтобы получить более точные результаты в расчете периметра фигуры, необходимо использовать точные формулы и методы, которые учитывают все особенности формы и структуры фигуры. Это может включать использование математических методов, численных методов или компьютерного моделирования.
В итоге, правильный выбор метода для расчета периметра фигуры зависит от сложности формы и требуемой степени точности. Простая формула может быть достаточной для простых фигур, но для сложных и нестандартных случаев, необходимы более сложные и точные методы.
Точная формула для периметра фигуры: когда и как правильно использовать
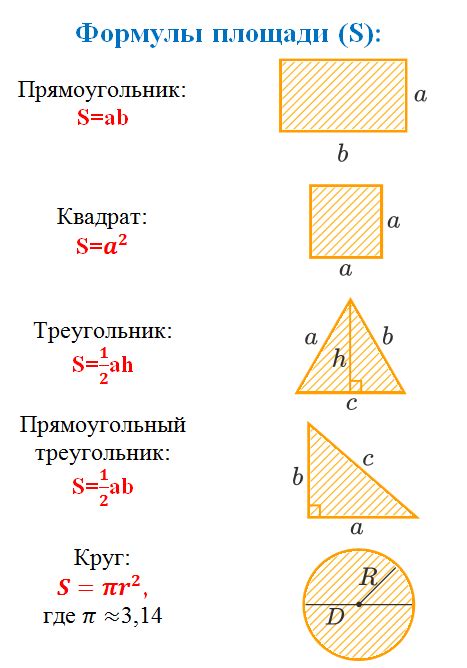
Точная формула для периметра фигуры может быть представлена различными математическими уравнениями, в зависимости от типа фигуры.
Круг: периметр круга равен произведению его диаметра на число π (пи). Формула периметра круга: P = 2πr, где P – периметр, r – радиус круга.
Прямоугольник: периметр прямоугольника равен удвоенной сумме длин его сторон. Формула периметра прямоугольника: P = 2(a + b), где P – периметр, a и b – длины сторон прямоугольника.
Треугольник: периметр треугольника равен сумме длин его трех сторон. Формула периметра треугольника: P = a + b + c, где P – периметр, a, b и c – длины сторон треугольника.
Использование точной формулы для периметра фигуры позволяет получить более точный и достоверный результат, чем при использовании простого метода. Важно помнить, что для каждого типа фигуры существует своя формула, и ее необходимо использовать в соответствии с конкретной задачей.
Сравнение простого метода и точной формулы: что выбрать?

При расчете периметра и площади фигур можно использовать простой метод или точную формулу. Каждый из этих методов имеет свои особенности, и выбор одного из них зависит от конкретной задачи.
- Простой метод: Этот метод подходит для простых фигур, таких как квадраты, прямоугольники и круги. Он заключается в прямом измерении сторон фигуры и их последующем сложении или использовании простой формулы. Этот метод быстр и легок в использовании, особенно если у вас нет точной формулы под рукой.
- Точная формула: Использование точной формулы требует знания математических соотношений между различными параметрами фигуры. Он подходит для более сложных фигур, например, треугольников и эллипсов. Использование точной формулы позволяет получить более точные и надежные результаты, особенно когда требуется большая точность или когда нельзя прямо измерить стороны фигуры.
В общем, если у вас есть простая фигура с известными сторонами, вы можете использовать простой метод для быстрого расчета периметра и площади. Однако при работе с более сложными фигурами или требованиями к точности рекомендуется использовать точную формулу.
Выбор между простым методом и точной формулой зависит от вашей конкретной ситуации и требований к результатам расчетов. Важно помнить, что точность и надежность результатов достигаются путем использования подходящего метода и правильного применения соответствующих формул.