Арифметическая прогрессия - одно из основных понятий алгебры, которое представляет собой последовательность чисел, в которой каждый следующий элемент получается прибавлением к предыдущему одинакового числа. Важным аспектом арифметической прогрессии является сумма ее элементов, которая интересует многих математиков и учеников. Как найти сумму чисел арифметической прогрессии? В этой статье мы рассмотрим формулы расчета и приведем примеры.

Формула для расчета суммы элементов арифметической прогрессии имеет несколько видов, в зависимости от того, какая информация известна. Но основная формула для нахождения суммы N элементов арифметической прогрессии выглядит так:

S_N = (а₁ + а_n) * N / 2

где S_N - сумма N элементов прогрессии, а₁ - первый элемент прогрессии, а_n - n-й элемент прогрессии, N - количество элементов в прогрессии.

Давайте рассмотрим пример для более ясного представления. Пусть у нас есть арифметическая прогрессия с первым элементом 3, шагом 2 и количеством элементов 5. Найдем сумму элементов этой прогрессии:

S₅ = (3 + 3 + 2*4) * 5 / 2 = 30

Таким образом, сумма элементов данной прогрессии равна 30.

Арифметическая прогрессия: определение и примеры

Общий вид арифметической прогрессии:

an = a1 + (n-1)d

Здесь an - n-й член последовательности, a1 - первый член, d - разность между соседними членами.

Примеры арифметических прогрессий:

1. Прогрессия с первым членом 2 и разностью 3:

• 2, 5, 8, 11, 14, ...

• -1, -3, -5, -7, -9, ...

• 4, 4, 4, 4, 4, ...

Важным свойством арифметической прогрессии является то, что с помощью формулы можно найти сумму первых n членов прогрессии:

S_n = (n/2)(a1 + an),

где S_n - сумма первых n членов, a1 - первый член, an - n-й член.

Например, для первых 5 членов прогрессии 2, 5, 8, 11, 14 сумма будет:

S_5 = (5/2)(2 + 14) = 40.

Что такое арифметическая прогрессия?

Арифметическая прогрессия обозначается как (a, a + d, a + 2d, a + 3d, ...), где a - первый член прогрессии, а d - разность прогрессии.

Разность прогрессии может быть положительным, отрицательным или нулевым числом. В случае положительной разности прогрессия будет возрастающей, в случае отрицательной - убывающей, а в случае нулевой разности - константной.

В арифметической прогрессии можно найти любое число, если известны ее первый член и разность. Кроме того, можно найти сумму всех чисел прогрессии - такую сумму называют частичной суммой или суммой арифметической прогрессии.

Формула для нахождения суммы арифметической прогрессии выглядит следующим образом:

S_n = (n/2)(2a + (n-1)d)

где S_n - частичная сумма прогрессии, n - количество членов прогрессии, a - первый член прогрессии, d - разность прогрессии.

Например, для арифметической прогрессии (2, 5, 8, 11, 14) с разностью d = 3 и количеством членов n = 5, сумма прогрессии будет равна:

S₅ = (5/2)(2 * 2 + (5-1) * 3) = 25.

Таким образом, сумма арифметической прогрессии (2, 5, 8, 11, 14) равна 25.

Формула для расчета суммы чисел арифметической прогрессии

Формула для расчета суммы чисел арифметической прогрессии имеет вид:

S_n = (a₁ + a_n) / 2 * n

где S_n - сумма чисел арифметической прогрессии,

a₁ - первый член прогрессии,

a_n - последний член прогрессии,

n - количество членов прогрессии.

Формула даёт возможность легко и быстро вычислить сумму чисел арифметической прогрессии без необходимости отдельно складывать каждое число вручную.

Рассмотрим пример:

У нас есть арифметическая прогрессия, начинающаяся с числа 2 и с разностью 3. Мы хотим найти сумму первых 5 членов прогрессии.

Первый член прогрессии: a₁ = 2

Количество членов прогрессии: n = 5

Последний член прогрессии можно найти с помощью формулы: a_n = a₁ + (n - 1) * d, где d - разность прогрессии.

Подставляем значения в формулу для расчета суммы чисел арифметической прогрессии:

S₅ = (2 + (2 + 3 * (5 - 1))) / 2 * 5

S₅ = (2 + (2 + 3 * 4)) / 2 * 5

S₅ = (2 + (2 + 12)) / 2 * 5

S₅ = (2 + 14) / 2 * 5

S₅ = 16 / 2 * 5

S₅ = 8 * 5

S₅ = 40

Таким образом, сумма первых 5 членов данной арифметической прогрессии равна 40.

Как вычислить сумму чисел арифметической прогрессии?

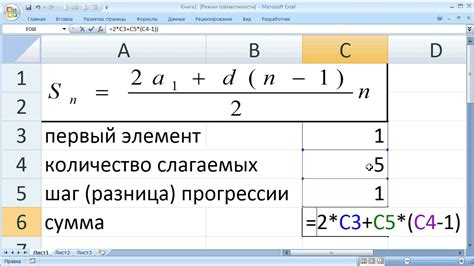
Сумма чисел арифметической прогрессии может быть вычислена при помощи специальной формулы. Формула обеспечивает быстрое и точное получение результата без необходимости суммирования каждого числа в отдельности.

Формула для вычисления суммы чисел арифметической прогрессии имеет вид:

S_n = (a₁ + a_n) * n / 2,

где S_n - сумма чисел прогрессии,

a₁ - первый член прогрессии,

a_n - последний член прогрессии,

n - количество членов прогрессии.

Таким образом, чтобы вычислить сумму чисел прогрессии, необходимо знать первый и последний члены прогрессии, а также количество членов.

Пример:

Допустим, дана арифметическая прогрессия с первым членом a₁ = 2, последним членом a_n = 10 и количеством членов n = 5. Давайте вычислим сумму чисел этой прогрессии:

S₅ = (2 + 10) * 5 / 2 = 12 * 5 / 2 = 60 / 2 = 30

Таким образом, сумма чисел арифметической прогрессии будет равна 30.

Примеры расчета суммы чисел арифметической прогрессии

Допустим, у нас есть арифметическая прогрессия, в которой первый член равен 3, разность равна 2, и мы хотим найти сумму первых 5 членов.

1) Для начала, найдем пятый член прогрессии. Используя формулу общего члена, находим:

a₅ = a₁ + (n - 1)d

= 3 + (5 - 1) * 2

= 3 + 8

= 11

2) Теперь мы можем использовать формулу суммы арифметической прогрессии для нахождения суммы первых 5 членов:

S₅ = (n/2) * (2a₁ + (n - 1)d)

= (5/2) * (2 * 3 + (5 - 1) * 2)

= (5/2) * (6 + 8)

= (5/2) * 14

= 35

Таким образом, сумма первых 5 членов данной арифметической прогрессии равна 35.

Приведенный выше пример демонстрирует, как использовать формулы для расчета суммы чисел арифметической прогрессии. Важно помнить, что формулы могут быть применены не только к примерам с пятью членами, но и к прогрессиям любой длины.

Практические примеры расчета суммы чисел арифметической прогрессии

Рассмотрим несколько примеров расчета суммы чисел арифметической прогрессии, чтобы лучше понять применение соответствующих формул.

1. Пример 1:

   Найдем сумму первых 5 членов арифметической прогрессии, если первый член равен 2, а разность равна 3.

   Сначала найдем пятый член прогрессии:

   Пятый член = первый член + (5 - 1) * разность = 2 + 4 * 3 = 14.

   Теперь можем воспользоваться формулой для расчета суммы первых n членов арифметической прогрессии:

   Сумма = (количество членов / 2) * (первый член + последний член) = (5 / 2) * (2 + 14) = 5 * 8 = 40.

   Таким образом, сумма первых 5 членов арифметической прогрессии равна 40.

2. Пример 2:

   Найдем сумму всех членов арифметической прогрессии, если первый член равен -3, разность равна 2 и количество членов равно 10.

   Сначала найдем последний член прогрессии:

   Последний член = первый член + (количество членов - 1) * разность = -3 + (10 - 1) * 2 = -3 + 18 = 15.

   Теперь можем воспользоваться формулой для расчета суммы всех членов арифметической прогрессии:

   Сумма = (количество членов / 2) * (первый член + последний член) = (10 / 2) * (-3 + 15) = 5 * 12 = 60.

   Таким образом, сумма всех членов арифметической прогрессии равна 60.

3. Пример 3:

   Найдем сумму четных чисел арифметической прогрессии, если первый член равен 2, разность равна 4 и количество членов равно 6.

   Сначала найдем последний член прогрессии:

   Последний член = первый член + (количество членов - 1) * разность = 2 + (6 - 1) * 4 = 2 + 20 = 22.

   Теперь можем воспользоваться формулой для расчета суммы первых n членов арифметической прогрессии:

   Сумма = (количество членов / 2) * (первый член + последний член) = (6 / 2) * (2 + 22) = 3 * 24 = 72.

   Таким образом, сумма четных чисел арифметической прогрессии равна 72.

Таким образом, формулы для расчета суммы чисел арифметической прогрессии позволяют быстро находить сумму определенных членов или всех членов прогрессии по известным данным. Это очень полезное свойство в различных областях математики, физики и экономики.