Косинус угла наклона – это математическое понятие, которое нашло применение в различных сферах деятельности. Он широко используется в инженерии, физике, геометрии и других науках для решения сложных задач и проведения расчетов. С пониманием и применением этого понятия связаны эффективные методы и подходы, которые позволяют решать разнообразные технические и научные задачи с высокой точностью.
Один из основных примеров использования косинуса угла наклона – расчет нагрузки на наклонные плоскости. Он позволяет определить, какая часть силы, действующей вертикально на плоскость, направлена по наклону. Этот расчет необходим, например, при проектировании склонов дорог, крутых лестниц или других конструкций, имеющих определенный угол наклона.
Также косинус угла наклона находит свое применение в геодезии и картографии. С его помощью можно определить изменение высоты в зависимости от изменения расстояния по наклонной поверхности. Это особенно полезно при составлении геометрических привязок, высотных планов и других геодезических работах, где необходимо учитывать наклон поверхности.
Расчеты косинуса угла наклона
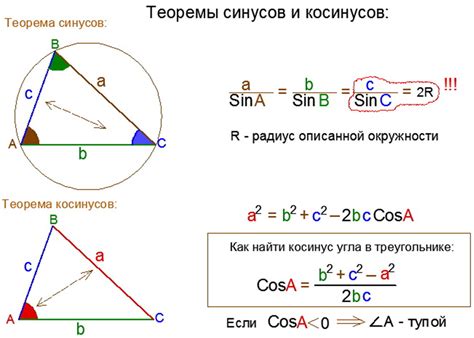
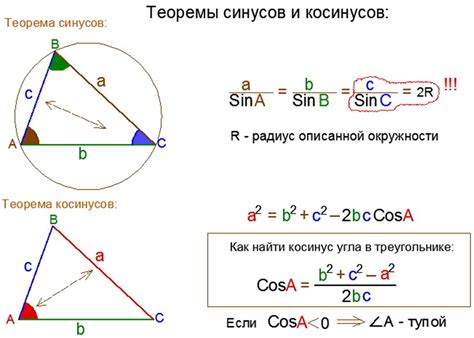
Расчет косинуса угла наклона осуществляется по формуле:
cos(α) = Adjacent / Hypotenuse
где:
- cos(α) - косинус угла наклона;
- Adjacent - длина стороны прилегающей к углу;
- Hypotenuse - длина гипотенузы.
Для расчета косинуса угла наклона необходимо знать значения этих двух величин. После подстановки их значений в формулу и выполнения арифметических операций можно определить косинус угла наклона.
Значение косинуса угла наклона находится в диапазоне от -1 до 1. Если значение равно -1, это означает максимальный уклон вниз. Если значение равно 1, это означает максимальный уклон вверх. Значение равное 0, говорит о горизонтальном положении объекта или поверхности.
Расчеты косинуса угла наклона находят широкое применение в различных областях, таких как геология, строительство, архитектура, аэрокосмическая промышленность, компьютерная графика и др. Это позволяет определить угол наклона для создания точных и эффективных расчетов, проектирования и моделирования.
Косинус угла наклона в геодезии
Косинус угла наклона часто используется в геодезии для решения различных задач, связанных с определением уклона земной поверхности. Этот математический инструмент позволяет оценить наклонные углы и наклонные расстояния, а также проводить расчеты высот на базе собранных геодезических данных.
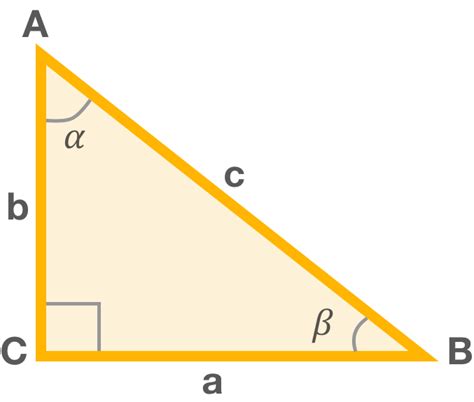
Косинус угла наклона задается формулой:
cos α = Δh / d
где α - угол наклона, Δh - изменение высоты, d - горизонтальное расстояние между точками.
Используя косинус угла наклона, геодезисты могут определить разницу высот (высотный уклон) между двумя точками или участком поверхности. Это особенно важно при проведении работ по проектированию и строительству дорог, трубопроводов, линий электропередач и других инженерных сооружений.
| Изменение высоты, Δh (м) | Горизонтальное расстояние, d (м) | Косинус угла наклона, cos α |
|---|---|---|
| 10 | 100 | 0.10 |
| 20 | 200 | 0.10 |
| 30 | 300 | 0.10 |
Приведенная выше таблица демонстрирует примеры расчета косинуса угла наклона для разных значений изменения высоты и горизонтального расстояния.
Необходимо отметить, что косинус угла наклона не является единственным или исчерпывающим инструментом для работы с горизонтальными и вертикальными координатами. В геодезии также используются другие методы, такие как тангенс угла наклона, синус угла наклона и т.д., в зависимости от поставленных задач и доступных данных.
Применение косинуса угла наклона в физике
- Расчет силы трения: Косинус угла наклона применяется при расчете силы трения, действующей на тело, которое перемещается по наклонной поверхности. С помощью косинуса угла наклона можно определить вертикальную и горизонтальную составляющие силы трения, что позволяет более точно оценить ее воздействие.
- Определение угла отражения: Когда свет или другие электромагнитные волны отражаются от поверхности, косинус угла наклона может быть использован для определения угла отражения. Это позволяет предсказать направление отраженного луча и, соответственно, его поведение при взаимодействии с другими объектами.
- Расчет работы при подъеме груза: При подъеме груза с помощью наклонной плоскости, косинус угла наклона используется для определения работы, которая должна быть выполнена для перемещения груза вверх. Расчеты с использованием косинуса угла наклона позволяют эффективно планировать и оптимизировать работу с механизмами подъема.
Таким образом, косинус угла наклона является неотъемлемым инструментом при проведении физических расчетов и определении различных физических характеристик. Он позволяет учитывать влияние угла наклона на различные процессы и явления, что существенно улучшает точность анализа и прогнозирования.
Расчеты косинуса угла наклона в графическом дизайне
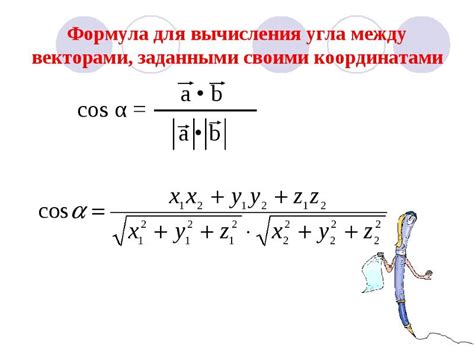
Для расчета косинуса угла наклона в графическом дизайне необходимо знать значения двух сторон треугольника, образованного объектом и горизонтальной осью координат. Для удобства, значения сторон треугольника могут быть представлены в виде координат X и Y двух точек, которые образуют отрезок.
Приложение графического дизайна может предоставлять удобный интерфейс для ввода координат X и Y точек объекта, а затем автоматически производить расчеты косинуса угла наклона. Результаты расчетов могут быть представлены в виде численного значения косинуса и визуализированы в виде графического отображения объекта с указанием его угла наклона.
| Стартовая точка | Конечная точка | Косинус угла наклона |
|---|---|---|
| (X1, Y1) | (X2, Y2) | cos(α) |
Расчеты косинуса угла наклона в графическом дизайне имеют широкий спектр применения. Они могут быть использованы для создания эффекта наклона текста или изображения, при верстке веб-страниц с использованием CSS3 трансформаций, а также для размещения и выравнивания элементов дизайна на печатных материалах или в графических редакторах.
Использование косинуса угла наклона в графическом дизайне дает возможность создавать эстетически привлекательные и сбалансированные композиции, а также повышает точность и профессионализм в работе дизайнера. Понимание и умение применять расчеты косинуса угла наклона позволяет создавать уникальные и впечатляющие графические проекты.
Косинус угла наклона в архитектуре
В процессе проектирования и строительства зданий, знание косинуса угла наклона является необходимым для определения оптимальных параметров, таких как угол наклона крыши, форма фасада, расположение окон и дверей. Это помогает создать гармоничный и функциональный объект.
Кроме того, косинус угла наклона используется при выборе материалов и конструкций, а также для определения требований к системам дренажа, освещения и вентиляции здания. Он влияет на энергоэффективность, солнцезащиту и уровень комфорта внутри помещений.
Применение косинуса угла наклона в архитектуре помогает спроектировать такие объекты, которые максимально соответствуют потребностям клиента, учитывая климатические и экологические условия. Расчеты с использованием этого параметра позволяют достичь оптимального баланса между эстетикой и функциональностью здания.
Программирование с использованием косинуса угла наклона

Одним из простых примеров применения косинуса угла наклона является вычисление расстояния между двумя точками на плоскости. Для этого необходимо определить вектор между точками и затем использовать косинус угла между этим вектором и осью для определения расстояния. Этот подход может быть полезен при разработке игр или географических приложений.
Еще одним интересным примером использования косинуса угла наклона является определение ориентации компонента визуализации на экране. Например, в 3D-графике можно использовать косинус угла наклона для определения, насколько наклонена поверхность относительно наблюдателя, что позволяет создавать реалистичные эффекты светотени и объемности.
Однако, при программировании с использованием косинуса угла наклона необходимо учитывать и некоторые ограничения. Во-первых, значения косинуса угла могут меняться от -1 до 1, поэтому важно проверять, что полученное значение находится в этом диапазоне, чтобы избежать ошибок при вычислениях. Во-вторых, использование косинуса угла наклона требует работы с градусами или радианами, поэтому необходимо уметь конвертировать значения из одной системы в другую.
В целом, программирование с использованием косинуса угла наклона является мощным инструментом, который может существенно облегчить решение разнообразных задач. Правильное использование этого математического понятия позволяет создавать более эффективные и точные приложения, открывая новые возможности для программистов и разработчиков.
Косинус угла наклона в приложениях для мобильных устройств
Одним из основных применений косинуса угла наклона в мобильных приложениях является определение ориентации устройства. С помощью встроенных акселерометров и гироскопов, мобильные устройства могут определить угол наклона относительно горизонта и вертикали. Это позволяет создавать интересные и интерактивные приложения, такие как игры, навигационные программы и многое другое.
Косинус угла наклона также находит применение в различных геометрических расчетах. Например, в приложениях для измерения расстояний и высот используется техника треугольной тригонометрии, в которой косинус угла наклона играет важную роль. С его помощью можно определить высоту здания, длину объекта или даже глубину водоема.
В физических приложениях косинус угла наклона помогает решать задачи, связанные с наклонными плоскостями, силами трения и поверхностным натяжением. Например, в спортивных приложениях такие расчеты используются для определения угла наклона пола во время скейтбординга, катания на горных лыжах или сноуборде. Это позволяет создавать реалистичные физические эффекты и повышать уровень вовлеченности пользователя.