Логарифмические функции являются одной из основных составляющих алгебры и математического анализа. Они используются для различных целей, от моделирования роста и децибелов до решения уравнений и анализа алгоритмов.
Одним из важных моментов при работе с логарифмическими функциями является поиск аргумента нуля. Аргумент нуля - это значение, при котором логарифмическая функция обращается в ноль. Важность такого поиска связана с необходимостью решения уравнений и нахождения точек пересечения кривых и осей координат.
Существует несколько способов нахождения аргумента нуля логарифмической функции. Один из них основан на понимании основного свойства логарифма. Если логарифм равен нулю, то его аргумент равен единице. Поэтому, чтобы найти аргумент нуля, нужно решить уравнение, где логарифм равен нулю, и найти его значение.
Методы нахождения аргумента нуля
1. Графический метод
Один из наиболее простых способов определения аргумента нуля - построение графика функции и определение точки пересечения с осью абсцисс. Для этого можно использовать программы для построения графиков, калькуляторы или математические пакеты.
2. Аналитический метод
При использовании аналитического метода нахождения аргумента нуля нужно записать исходное уравнение функции и решить его с учетом условия, что функция обращается в ноль. Так, для логарифмической функции можно записать уравнение вида ln(x) = 0 и решить его, найдя значение x.
3. Итерационный метод
Если аргумент нуля не может быть найден аналитически, можно использовать итерационный метод. Этот метод заключается в выборе начального значения аргумента и последовательном приближении к аргументу нуля путем выполнения итераций с помощью специальной формулы или алгоритма.
В зависимости от сложности функции, ее свойств и доступных инструментов, выбор метода нахождения аргумента нуля может различаться. Комбинирование разных методов или использование специализированных программных средств может помочь упростить и ускорить процесс нахождения аргумента нуля логарифмической функции.
Применение логарифма в поиске аргумента нуля

Поиск аргумента нуля логарифмической функции – это нахождение значения x, при котором функция принимает значение 0. Важным свойством логарифма является то, что логарифм от числа 1 равен 0, то есть logb(1) = 0. Именно это свойство мы будем использовать в поиске аргумента нуля.
Для того чтобы найти аргумент нуля логарифмической функции, нужно решить уравнение logb(x) = 0. Из свойства логарифма, это уравнение эквивалентно уравнению b0 = x, что равносильно уравнению 1 = x. Таким образом, аргументом нуля логарифмической функции будет число 1.
Применение логарифма в поиске аргумента нуля основано на алгоритмическом свойстве логарифма и является одним из простых способов нахождения данного значения. Оно особенно полезно при решении задач, связанных с экспоненциальным ростом или убыванием, а также для нахождения точек пересечения графиков функций.
В таблице ниже даны некоторые базы логарифма и их значения для аргумента нуля:
| База логарифма (b) | Значение аргумента нуля (x) |
|---|---|
| 2 | 1 |
| 10 | 1 |
| e (природный логарифм) | 1 |
Таким образом, при использовании логарифма для поиска аргумента нуля, значение x будет равно 1 для всех баз логарифма.
Свойства логарифмической функции для определения аргумента нуля

Свойство логарифмической функции, которое позволяет нам определить аргумент нуля, заключается в следующем:
Если логарифмическая функция равна нулю, то аргумент такой функции будет равен единице.
Другими словами, если y = logb(x) и y = 0, то x = 1.
Определение аргумента нуля может быть полезным при решении уравнений, в которых встречается логарифмическая функция. Нахождение аргумента нуля позволяет нам узнать точку пересечения графика функции с осью абсцисс.
Используя данное свойство, мы можем решить уравнение logb(x) = 0. Подставляя значение 0 вместо y, получаем уравнение logb(x) = 0. Согласно свойству, аргументом этой функции будет x = 1.
Таким образом, зная свойства логарифмической функции, мы можем определить аргумент нуля и использовать это знание для решения уравнений и построения графиков функций.
Графическое представление логарифмической функции и поиск аргумента нуля
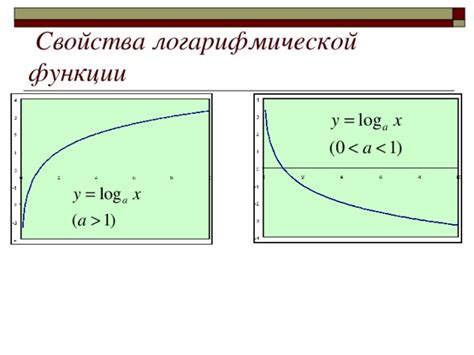
Чтобы построить график логарифмической функции, необходимо знать ее основание. Часто используется естественный логарифм с основанием e, обозначаемый как ln(x). График такой функции будет проходить через точку (1, 0) и стремиться к оси абсцисс по мере увеличения значения аргумента.
На графике логарифмической функции можно определить аргумент нуля – значение аргумента, при котором функция равна нулю. Для этого необходимо найти точку пересечения графика функции с осью абсцисс. Если у функции есть аргумент нуля, то это будет точка пересечения графика с осью x, в которой значение y равно 0.
Для поиска аргумента нуля можно использовать различные методы. Один из них – графический метод. При помощи графика функции можно приближенно определить значение аргумента, при котором функция равна нулю. Для этого необходимо проследить график функции и найти точку, где он пересекает ось x или близко к ней.
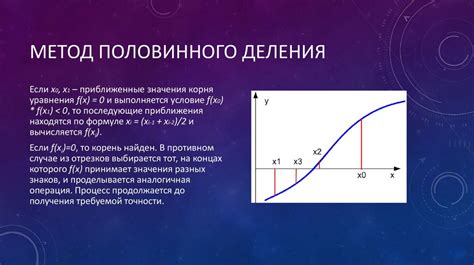
Если графический метод не дает точного результата, можно использовать численные методы для более точного определения аргумента нуля логарифмической функции, например, метод половинного деления или метод Ньютона.
Графическое представление логарифмической функции и поиск аргумента нуля являются важными инструментами для анализа и решения различных задач, связанных с логарифмическими функциями. Эти методы позволяют определить точное значение аргумента нуля и использовать его в дальнейших вычислениях и приложениях.