Равновесие рычага – один из фундаментальных принципов механики, который широко применяется в различных областях науки и техники. Этот принцип основывается на законах физики и позволяет понять, как объекты взаимодействуют друг с другом и находят свое равновесие.
Основная идея равновесия рычага состоит в том, что объекты находятся в равновесии, когда моменты сил, действующих на них, сбалансированы. Момент силы вычисляется как произведение силы на расстояние до оси вращения. Используя этот принцип, можно определить, какой вес нужно поднять или какую силу нужно приложить к определенному пункту, чтобы достичь равновесия системы.
Равновесие рычага находит свое применение во многих областях. Например, в механике и строительстве, равновесие рычага используется для расчета необходимой силы, чтобы поддерживать определенное положение объекта или конструкции. В аэронавтике этот принцип помогает определить, какая сила нужна для управления самолетом или ракетой. Даже в бытовой сфере принцип равновесия рычага используется при работе с весами и различными механизмами.
Равновесие рычага: основные принципы
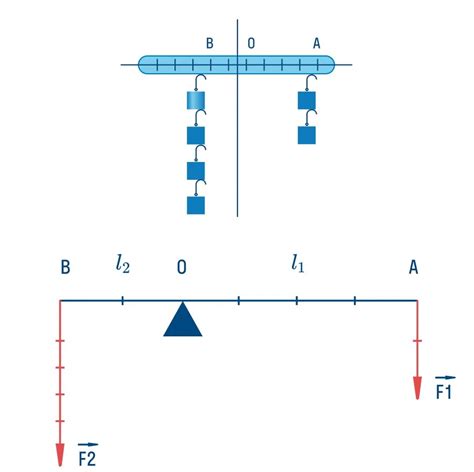
Основными принципами равновесия рычага являются:
- Закон моментов сил. Согласно этому закону, момент силы, действующей на одном из концов рычага, равен моменту силы, действующей на другом конце. Для достижения равновесия необходима балансировка моментов сил, что позволяет рычагу оставаться неподвижным.
- Разделение нагрузки и усилия. Рычаг позволяет усилить силу, применяемую для поднятия или передвижения нагрузки. Это достигается за счет разделения усилия на две составляющие: усилие, приложенное к рычагу, и усилие, применяемое к нагрузке. Соответствующая позиция точки опоры рычага позволяет достичь оптимального равновесия между этими усилиями.
- Правило моментов. Согласно данному правилу, момент силы равен произведению силы на плечо. Для достижения равновесия рычага необходимо, чтобы момент силы, действующей на одном из концов, был равен моменту силы на другом конце рычага.
Равновесие рычага широко применяется в практике, включая машиностроение, строительство, биомеханику, а также в повседневной жизни. Понимание основных принципов равновесия рычага позволяет эффективно использовать его в различных сферах, обеспечивая устойчивость и усиление усилия.
Принцип моментов сил
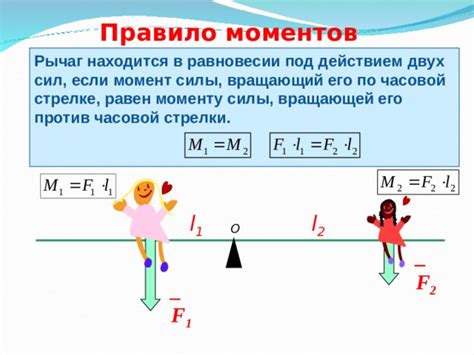
Согласно принципу моментов сил, уравновешенный рычаг должен удовлетворять условию ∑M = 0, где ∑M - сумма моментов сил относительно некоторой оси вращения.
Момент силы определяется как произведение силы на плечо, то есть расстояние от оси вращения до точки приложения силы. При применении принципа моментов сил необходимо учесть знаки момента силы: положительный момент означает вращение против часовой стрелки, отрицательный - по часовой стрелке.
Принцип моментов сил широко применяется в практике при решении задач на механику и конструирование механизмов. Он позволяет определить равновесие системы, а также рассчитать неизвестные силы, приложенные к рычагу или другим элементам механизма.
Принцип моментов сил также используется при проектировании различных механизмов, таких как рычаги, маятники, краны и др. Знание и применение этого принципа позволяет улучшить эффективность работы механизмов и обеспечить их надежное функционирование.
Зависимость равновесия от распределения массы рычага

При равномерном распределении массы на рычаге, центр тяжести будет находиться в середине его длины. В таком случае, равновесие системы достигается, когда сумма моментов сил, действующих на рычаг, равна нулю. Это можно выразить следующей формулой:
ΣF * r = 0
Где ΣF - сумма всех сил, действующих на рычаг, а r - расстояние от точки приложения силы до оси вращения. Если сумма моментов сил равна нулю, то рычаг находится в равновесии.
Однако, при неравномерном распределении массы на рычаге, центр тяжести будет смещаться относительно его оси вращения. В этом случае, равновесие системы достигается, когда момент сил, вызванный разницей в распределении массы, компенсируется другими силами.
Знание зависимости равновесия от распределения массы на рычаге позволяет проектировать более эффективные механические системы. Использование математических моделей и расчетов может помочь определить оптимальное распределение массы, которое обеспечит стабильное равновесие и эффективную работу системы.
Применение равновесия рычага в практике
Применение равновесия рычага в практике имеет множество примеров. Одним из таких примеров является использование рычага при подъеме тяжелых предметов. При правильном использовании рычага можно значительно снизить необходимую для подъема силу, уравновешивая силу, необходимую для поднятия предмета, силой, действующей в противоположном направлении.
Еще одним примером применения равновесия рычага является его использование в механизмах и машинах. Многие механизмы и машины основаны на принципе равновесия рычага, используя его для передачи и усиления силы. Такие применения равновесия рычага в практике позволяют создавать эффективные и надежные механизмы для различных целей.
Более простым примером применения равновесия рычага является использование его в плетении кос или корзин из веток. При плетении рычагом можно контролировать напряжение веток, достигая равновесия сил, действующих на плетение.
В целом, принцип равновесия рычага имеет широкое применение в практической деятельности и помогает решать различные проблемы, связанные с передачей и усилением силы, достижением равновесия и контролем напряжения. Понимание и применение этого принципа могут быть полезными во многих областях, включая механику, строительство, дизайн и другие.