Ромб - это особый четырехугольник, у которого все четыре стороны равны друг другу. Это привлекает внимание и вызывает интерес у математиков и геометров. В данной статье мы рассмотрим геометрические особенности ромба и узнаем, почему его стороны равны.
Первое, что стоит отметить, это то, что ромб является параллелограммом - фигурой, у которой противоположные стороны параллельны. Кроме того, все углы ромба равны между собой и составляют 90 градусов. Все эти свойства делают ромб особенным и интересным объектом изучения.
Причина равенства сторон ромба заключается в его симметрии. Каждая сторона ромба является отрезком, соединяющим две вершины ромба. Так как ромб имеет симметрию с разных сторон, то все его стороны равны друг другу. Это можно легко увидеть, нарисовав ромб и проведя линии симметрии. По этим линиям видно, что любая сторона ромба имеет ту же длину, что и другая.
Таким образом, равенство сторон ромба обусловлено его симметрией и особенностями внутренней структуры. Изучение этих геометрических особенностей помогает не только лучше понять ромб, но и расширять свои знания в области геометрии и математики в целом.
Геометрические особенности ромба
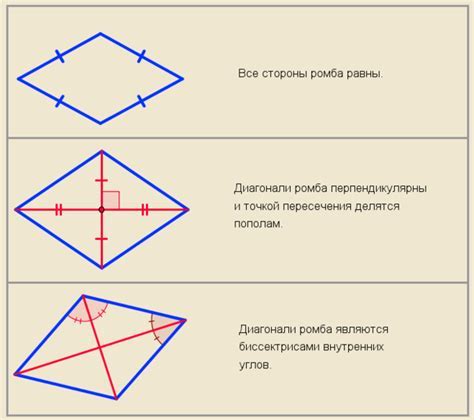
Другая важная геометрическая особенность ромба - у него противоположные углы равны. Таким образом, углы А и В, В и С, С и D, D и А равны между собой. Это означает, что каждый угол ромба составляет 90 градусов.
Также ромб обладает свойством существования диагоналей, которые делят его на четыре равных треугольника. Диагонали ромба AC и BD перпендикулярны друг другу и пересекаются в точке O, которая является центром симметрии ромба.
За счет своих геометрических особенностей, ромб используется не только в математике, но и в различных областях, таких как строительство, дизайн и графика. Его регулярные формы и симметричность делают его популярным элементом дизайна и символом равенства и справедливости.
Структура ромба в геометрии
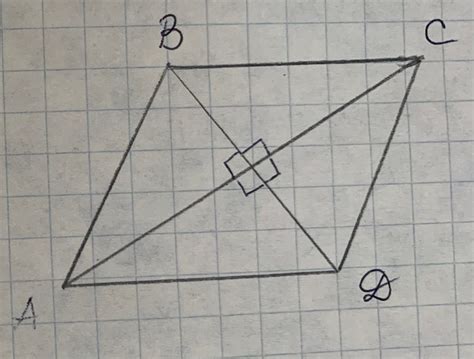
Основные элементы структуры ромба:
| 1. Стороны: | Ромб имеет четыре равные стороны. Это означает, что каждая сторона ромба имеет одинаковую длину. |
| 2. Углы: | Ромб имеет четыре равных угла. Все углы ромба равны между собой и равны 90 градусам. |
| 3. Диагонали: | Диагонали ромба являются важной частью его структуры. Диагонали ромба делят его на две равные треугольные части и пересекаются в центре ромба под прямым углом. |
| 4. Углы между диагоналями: | Углы между диагоналями ромба всегда равны 90 градусам. Это означает, что каждый из вершин ромба является прямым углом между его диагоналями. |
Структура ромба позволяет ему обладать рядом особенностей, которые делают его полезным в различных областях. Например, равные стороны ромба позволяют использовать его для создания симметричных и красивых узоров в рисовании и дизайне. Кроме того, свойство перпендикулярности сторон и углов ромба делает его полезным для решения задач на построение и нахождение неизвестных элементов в геометрии.
Свойства равных сторон ромба
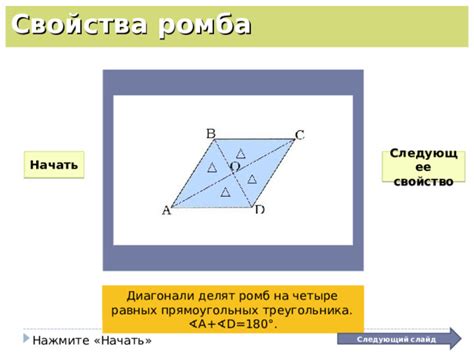
Одно из свойств равных сторон ромба – равенство всех диагоналей. Диагональ – это отрезок, соединяющий две противоположные вершины ромба. В связи с равенством сторон, все диагонали ромба имеют одинаковую длину. Это свойство является следствием равенства треугольников, образованных диагоналями и сторонами ромба.
Другое свойство равных сторон ромба – перпендикулярность диагоналей. В точках пересечения диагоналей ромба образуется пересекающий угол, который всегда равен 90 градусов. Это следует из того, что диагонали ромба являются биссектрисами его углов. Таким образом, равенство сторон ромба определяет его перпендикулярную структуру.
Важным свойством равных сторон ромба является симметрия фигуры относительно каждой из его диагоналей. Более того, каждая диагональ является осью симметрии для ромба. Это значит, что если отразить ромб относительно одной из диагоналей, то полученная фигура будет совпадать с исходным ромбом.
Другие важные свойства равных сторон ромба включают равенство всех углов ромба (каждый угол равен 90 градусам) и параллельность противоположных сторон ромба.
Свойства равных сторон ромба являются основой для решения различных геометрических задач, а также позволяют установить связи между ромбом и другими геометрическими фигурами.
Углы в ромбе и их взаимосвязь

В ромбе все углы равны между собой. Это свойство называется "свойством равных углов в ромбе".
Пусть $\angle ABC$ - один из углов ромба. Из свойства равных углов следует, что каждый угол ромба равен $\angle ABC$.
Также в ромбе две пары противоположных углов являются смежными и дополнительными. Это означает, что сумма смежных углов ромба равна 180 градусов.
Таким образом, углы в ромбе обладают следующими свойствами:
- Все углы ромба равны между собой.
- Сумма смежных углов ромба равна 180 градусов.
Доказательство равенства сторон в ромбе
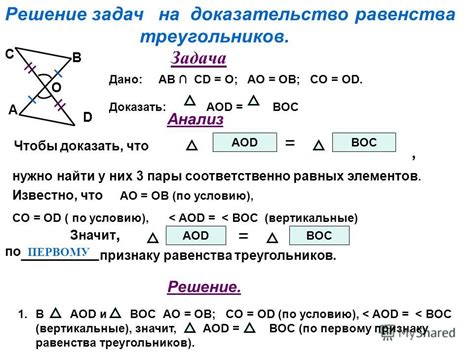
Чтобы доказать, что все стороны ромба равны между собой, можно воспользоваться его определением. Ромб - это четырехугольник, у которого все стороны имеют одинаковую длину. Это означает, что все стороны ромба равны друг другу.
Существует несколько способов доказательства равенства сторон в ромбе. Один из них основан на равенстве противоположных сторон. Пусть AB и CD - диагонали ромба, a и b - их длины соответственно. Тогда можно сказать, что треугольники ABD и BCD подобны, так как у них имеются две пары равных углов, а стороны AB и CD общие.
Используя свойство подобных треугольников, имеем соотношение:
a/b = b/a
Упростив выражение, получаем:
a2 = b2
Таким образом, длины диагоналей ромба должны быть равны между собой.
Поскольку все диагонали ромба равны между собой, а диагональ - это отрезок, соединяющий две противоположные вершины, то следует, что все стороны ромба должны быть равны между собой.
Таким образом, мы доказали, что в ромбе все стороны равны друг другу. Это важное свойство ромба помогает различать его от других четырехугольников и использовать его в различных математических и геометрических задачах.
Причины равенства сторон и углов в ромбе

Основная причина равенства сторон в ромбе - это специфическое расположение его вершин. Все вершины ромба находятся на одинаковом расстоянии от его центра. Это означает, что каждая сторона ромба может быть рассмотрена как радиус окружности, вписанной в него. Радиусы всех этих окружностей равны между собой, и поэтому все стороны ромба равны.
Как следствие равенства сторон, углы ромба также оказываются равными. Равенство сторон позволяет установить, что все диагонали ромба пересекаются в его центре и делятся пополам. Это означает, что любая диагональ ромба является осью симметрии для него. Когда диагональ делит ромб на два треугольника, они оказываются равнобедренными с равными углами у основания. Поэтому в ромбе все углы равны между собой.
Таким образом, причина равенства сторон и углов в ромбе заключается в его особой геометрии, в которой все вершины находятся на равном расстоянии от центра. Это свойство делает ромб уникальной фигурой, которая имеет ряд применений в геометрии и практической математике.
| Свойство | Причина равенства |
| Равенство сторон | Вершины ромба находятся на одинаковом расстоянии от его центра |
| Равенство углов | Все диагонали ромба пересекаются в его центре и делятся пополам |
Применение равности сторон ромба в практических задачах

Равная длина всех сторон ромба вносит некоторые интересные преимущества и позволяет использовать это геометрическое свойство в различных практических задачах. Рассмотрим несколько примеров, где равные стороны ромба играют важную роль.
1. Архитектура зданий: при проектировании зданий часто используются ромбовидные элементы, такие как окна, двери или витрины. Использование ромбов позволяет достичь баланса и гармонии в дизайне здания, а также обеспечивает стабильность и прочность конструкции.
2. Укладка плитки: равные стороны ромба позволяют легко и красиво укладывать плитку. Благодаря одинаковой длине сторон ромба, можно получить равномерный и гармоничный узор. Это особенно полезно при укладке плитки на больших площадях, таких как полы в торговых центрах или аэропортах.
3. Раскрой материалов: если у вас есть материалы, такие как ткань или кожа, и вам необходимо раскроить их на равные детали, то использование ромбовых форм может помочь. Благодаря равным сторонам ромба вы сможете более эффективно использовать материал и избежать его излишнего расхода, что нередко возникает при раскрое на другие формы.
4. Решение задач по геометрии: в задачах по геометрии равество сторон ромба может быть полезным для нахождения других геометрических параметров. Например, используя свойство, что диагонали ромба перпендикулярны и делят его на 4 равных треугольника, можно найти различные углы и длины диагоналей.
Таким образом, равные стороны ромба имеют широкое применение в практических задачах, связанных со строительством, дизайном, раскроем материалов и решением геометрических задач. Понимание и использование этого геометрического свойства может быть полезным при проектировании и решении различных задач в повседневной жизни.



