Площадь фигуры - это важная характеристика геометрической фигуры, которая позволяет определить площадь поверхности этой фигуры. Знание формул для вычисления площадей различных фигур является необходимым для решения многих задач из разных областей, таких как архитектура, строительство, география и другие. Если вы хотите научиться находить площадь различных фигур, то вам понадобятся специальные формулы и несколько примеров.
Прямоугольник - одна из наиболее простых и понятных геометрических фигур. Его площадь находится по формуле: S = a * b, где a и b - длины двух противоположных сторон прямоугольника. Например, если длина a равна 5 см, а длина b равна 8 см, то площадь прямоугольника будет 40 квадратных сантиметров.
Круг - это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от центра. Площадь круга вычисляется по формуле: S = π * r^2, где π - число пи (около 3.14159), а r - радиус круга. Например, если радиус круга равен 10 см, то его площадь будет приблизительно равна 314.16 квадратных сантиметров.
Формулы для вычисления площади фигур
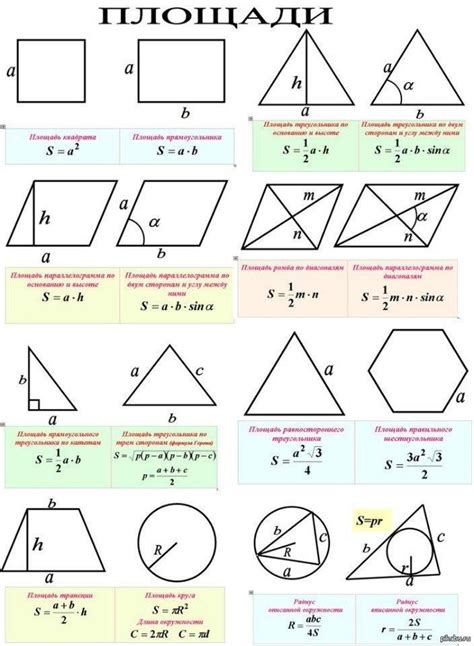
Вот некоторые из самых распространенных фигур и соответствующие им формулы для вычисления площади:
| Фигура | Формула для вычисления площади |
|---|---|
| Прямоугольник | Площадь = Длина * Ширина |
| Квадрат | Площадь = Сторона * Сторона |
| Треугольник | Площадь = (Основание * Высота) / 2 |
| Круг | Площадь = Пи * Радиус^2 |
| Тrapezium (Трапеция) | Площадь = (Сумма оснований * Высота) / 2 |
Это всего лишь некоторые из формул для вычисления площади фигур. В реальности их существует гораздо больше. Использование правильной формулы для расчета площади фигуры – это важный аспект в математике и приложении к реальному миру.
Надеюсь, эта информация помогла вам лучше понять, как найти площадь фигуры и какие формулы для этого использовать.
Площадь прямоугольника и квадрата
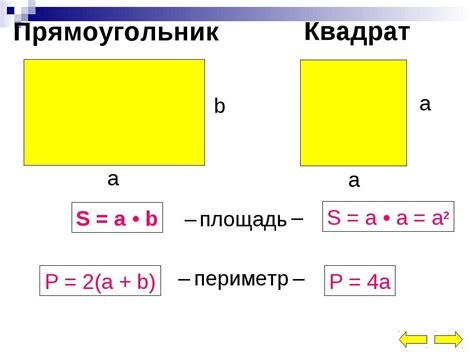
Формула для расчета площади прямоугольника: S = a * b, где S - площадь, а и b - длины сторон.
Квадрат - это частный случай прямоугольника, у которого все стороны одинаковой длины. Одна сторона квадрата называется ребром. Для нахождения площади квадрата нужно знать длину его ребра.
Формула для расчета площади квадрата: S = a * a, где S - площадь, a - длина ребра.
Площадь круга

S = π·r²
где S - площадь круга, π (пи) - математическая константа, равная приблизительно 3.14159, а r - радиус круга.
Чтобы найти площадь круга, необходимо знать его радиус и подставить его значение в формулу. После этого можно вычислить площадь, перемножив значение радиуса на квадрат π.
Пример:
| Радиус (r) | Площадь (S) |
|---|---|
| 5 | 78.54 |
| 8 | 201.06 |
| 10 | 314.16 |