Алгоритм quicksort является одним из наиболее эффективных и широко используемых методов сортировки. Несмотря на свою простоту, он обладает высокой скоростью работы и работает с линейной дополнительной памятью. QuickSort часто используется в языках программирования и во многих приложениях, где требуется сортировка массивов данных.
Принцип действия алгоритма quicksort основан на принципе "разделяй и властвуй". Он разбивает исходный массив на две подмассива, опорный элемент (pivot) выбирается таким образом, чтобы элементы меньше него находились слева, а элементы больше - справа. Затем процесс разбиения рекурсивно повторяется для каждого подмассива до тех пор, пока все элементы не будут отсортированы.
Статья описывает алгоритм quicksort с точки зрения его реализации и анализа его эффективности. В ней рассматриваются различные варианты выбора опорного элемента, методы разделения массива и оптимизация алгоритма для случаев, когда массив уже в значительной степени отсортирован. Автор также приводит исследования о времени выполнения алгоритма quicksort на разных типах данных и объясняет его сложность и устойчивость.
Быстрый обзор на алгоритм сортировки quicksort
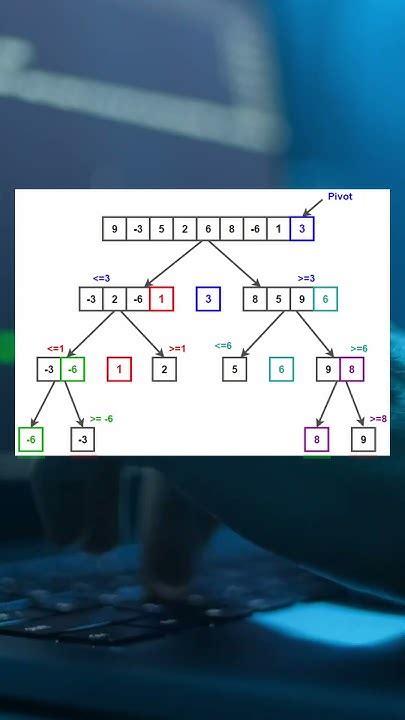
Основная идея алгоритма quicksort заключается в выборе опорного элемента из массива и разделении массива на две группы: элементы, меньшие опорного, и элементы, большие опорного. Затем происходит рекурсивное применение алгоритма к каждой из групп, до тех пор пока длина массива не станет равна 1 или 0.
Сложность алгоритма quicksort в среднем составляет O(n log n), что делает его одним из самых эффективных алгоритмов сортировки. Однако, в худшем случае, когда опорный элемент выбирается неоптимально, сложность может достигать O(n^2), что делает алгоритм менее эффективным.
Преимуществом алгоритма quicksort является его быстродействие и небольшое количество потребляемой памяти. Кроме того, алгоритм quicksort может быть эффективно реализован как на массивах, так и на связных списках.
Однако, недостатком алгоритма quicksort является его нестабильность. Это означает, что элементы, имеющие одно и тоже значение, могут менять свои относительные позиции в отсортированном массиве.
В целом, алгоритм quicksort является одним из наиболее эффективных алгоритмов сортировки, но требует оптимального выбора опорного элемента для достижения наилучшей производительности.
История возникновения и развития алгоритма quicksort

Алгоритм сортировки quicksort был разработан Британским ученым Тони Хоаром в 1960 году. Идея была в том, чтобы сортировать массив элементов путем последовательного выбора опорного элемента и разделения массива на подмассивы, меньшие и большие опорного значения.
Тони Хоар создал алгоритм quicksort во время работы над проектом по сортировке машинных кодов на одном из первых коммерческих компьютеров Ferranti Mercury. Он искал более эффективный способ сортировки больших объемов данных, который бы не требовал дополнительной памяти для хранения промежуточных результатов.
Первоначально quicksort алгоритм был реализован на языке машинных кодов, но позже был адаптирован для работы на других языках программирования. Несмотря на свою простоту и эффективность, quicksort был изначально менее известен, чем другие алгоритмы сортировки, такие как сортировка слиянием и сортировка пузырьком.
Однако, quicksort был быстрее и требовал меньше памяти для выполнения сортировки больших объемов данных. В результате, начиная с 1970-х годов, алгоритм quicksort стал широко использоваться и изучаться в университетах и в индустрии программирования.
В последующие годы, были разработаны различные вариации quicksort алгоритма, включая рандомизированный quicksort, который использует случайное выбор опорного элемента, и оптимизации для работы с большими или частично отсортированными массивами.
Сегодня алгоритм quicksort остается одним из наиболее популярных и широко используемых алгоритмов сортировки. Он широко применяется в различных областях, от сортировки данных в базах данных до сортировки элементов в программировании.
Работа алгоритма внутри: шаги и применяемые операции
Алгоритм сортировки quicksort использует стратегию "разделяй и властвуй". Основная идея заключается в разделении массива на две части: одну с элементами, меньшими или равными опорному, и вторую с элементами, большими опорного.
Шаги алгоритма:
- Выбор опорного элемента из массива.
- Разделение массива на две части: элементы, меньшие или равные опорному, и элементы, большие опорного.
- Рекурсивное применение алгоритма к обеим частями массива.
- Объединение отсортированных частей массива.
Применяемые операции:
| Операция | Описание |
|---|---|
| Выбор опорного элемента | Алгоритм выбирает опорный элемент в массиве, который будет использоваться для разделения массива на две части. |
| Разделение массива | Алгоритм проходит по массиву и распределяет элементы в соответствии с их отношением к опорному элементу. Элементы, меньшие или равные опорному, помещаются в одну часть массива, а элементы, большие опорного, - в другую часть. |
| Рекурсивное применение алгоритма | Алгоритм рекурсивно применяется к обеим частям массива до тех пор, пока размеры частей не станут равными нулю или единице. |
| Объединение отсортированных частей массива | После завершения рекурсивных вызовов, отсортированные части массива объединяются в один отсортированный массив. |
Алгоритм quicksort работает до тех пор, пока размер массива не станет равным нулю или единице. Каждый шаг алгоритма приводит к уменьшению размера массива в два раза, таким образом, алгоритм имеет временную сложность O(n log n) в среднем случае.
Сравнение quicksort с другими алгоритмами сортировки

Одно из главных преимуществ quicksort заключается в его скорости работы. В среднем случае, quicksort выполняется за время O(n log n), что делает его одним из самых эффективных алгоритмов сортировки.
Кроме того, quicksort требует небольшого дополнительного пространства для выполнения, что делает его удобным и экономически эффективным решением для сортировки больших массивов данных.
Однако quicksort не является устойчивым алгоритмом сортировки, что означает, что он не сохраняет относительный порядок элементов с одинаковыми значениями.
Тем не менее, quicksort может быть использован в сочетании с другими алгоритмами сортировки, чтобы обойти это ограничение и обеспечить устойчивую сортировку.
Например, можно использовать quicksort для разделения массива на подмассивы, а затем применить сортировку вставками к каждому подмассиву. Это позволит сохранить относительный порядок элементов с одинаковыми значениями.
Таким образом, quicksort является мощным и эффективным алгоритмом сортировки, который может быть оптимальным выбором для сортировки больших массивов данных, особенно если сохранение относительного порядка элементов с одинаковыми значениями не является важным условием.
Оценка времени выполнения и сложности алгоритма quicksort

Время выполнения алгоритма quicksort зависит от различных факторов, включая размер входных данных, выбор пивота и его положение в массиве. В лучшем случае, когда пивот находится всегда в середине массива, время выполнения составляет O(n log n), где n - количество элементов в массиве.
Однако, в худшем случае, когда пивот является наименьшим или наибольшим элементом массива, время выполнения может составлять O(n^2). Это происходит из-за несбалансированного разделения массива на подмассивы, что приводит к большому числу рекурсивных вызовов и сравнений элементов.
В среднем случае, время выполнения алгоритма quicksort составляет O(n log n), что является весьма эффективным, особенно при больших объемах данных. Время выполнения алгоритма может быть оценено с использованием метода рекуррентных соотношений и приближенных оценок.
Сложность алгоритма quicksort зависит от выбранной стратегии разделения и выбора пивота. Наиболее распространенной стратегией является выбор пивота с помощью случайной выборки, что позволяет достичь устойчивого времени выполнения в среднем случае.
Особенности и использование quicksort в реальных задачах
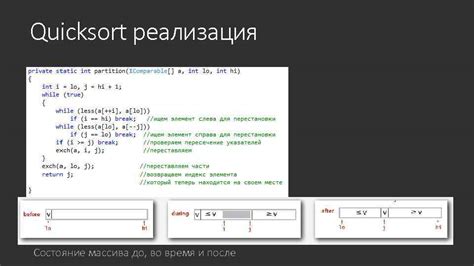
Quicksort использует метод "разделяй и властвуй", разбивая массив на подмассивы и рекурсивно сортируя их. Он основан на выборе "опорного элемента" и разделении массива на две части - элементы, меньшие и равные опорному, и элементы, большие опорного.
Одна из особенностей quicksort заключается в выборе опорного элемента. Классический алгоритм выбирает первый элемент массива, но это может привести к неэффективности в некоторых случаях, особенно когда массив уже отсортирован или содержит много повторяющихся элементов. Поэтому, чтобы улучшить производительность, рекомендуется использовать оптимизированные подходы к выбору опорного элемента, такие как случайный выбор или выбор медианы из нескольких элементов.
Quicksort может быть применен в широком спектре реальных задач, где требуется быстрая сортировка данных. Например:
- Сортировка списков - quicksort может быть использован для сортировки списков в практически любой области, где данные нужно упорядочить.
- Операции с базами данных - quicksort может быть использован для сортировки записей в базе данных, ускоряя выполнение запросов и улучшая производительность системы.
- Анализ данных - quicksort может быть применен для сортировки и анализа больших наборов данных, таких как данные сенсоров, данные клиентов и т.д.
Кроме того, quicksort используется во многих языках программирования и стандартных библиотеках для сортировки массивов и коллекций. Например, в языке Python функция sort() использует алгоритм quicksort для сортировки списков.
В целом, quicksort - мощный алгоритм сортировки, который может быть использован во множестве задач, где требуется эффективная и быстрая сортировка данных. Знание особенностей и применения этого алгоритма может помочь разработчикам создавать эффективные и оптимизированные приложения.
Алгоритм quicksort и его адаптации для различных языков программирования
QuickSort разработан в 1960 году английским ученым Тони Хоаром и с тех пор стал популярным алгоритмом сортировки благодаря своей эффективности и простоте реализации.
QuickSort в основном состоит из двух этапов: разделения и рекурсивной сортировки. В начале алгоритма выбирается опорный элемент, который используется для разделения массива на две части - одну с элементами, меньшими или равными опорному, и другую с элементами, большими опорного элемента. Затем происходит рекурсивная сортировка каждой из этих двух частей массива. Этот процесс повторяется до тех пор, пока весь массив не будет отсортирован.
Алгоритм QuickSort можно реализовать на различных языках программирования, и каждая реализация может варьироваться в деталях. Однако, идея и принципы алгоритма остаются неизменными. Некоторые языки программирования предоставляют встроенные функции для сортировки, основанные на алгоритме QuickSort, такие как функция qsort в языке C или метод sort в Python. В других языках программирования, таких как Java или JavaScript, алгоритм QuickSort может быть реализован с нуля, используя циклы и рекурсию.
Одно из важных преимуществ использования алгоритма QuickSort заключается в его эффективности. В среднем алгоритм QuickSort имеет время выполнения O(n log n), что делает его намного быстрее, чем некоторые другие алгоритмы сортировки, такие как сортировка пузырьком или сортировка вставками. Однако, в худшем случае время выполнения QuickSort может составлять O(n^2), что может произойти, например, если входной массив уже отсортирован в обратном порядке.
В итоге, алгоритм QuickSort и его адаптации для различных языков программирования являются важными инструментами для сортировки массивов. Понимание принципов и реализаций алгоритма QuickSort может помочь программистам написать более эффективные и оптимизированные алгоритмы сортировки на различных языках программирования.
Пример использования quicksort в практике

Алгоритм сортировки quicksort широко применяется в практическом программировании для упорядочивания массивов данных. Несмотря на то, что quicksort может быть сложен для понимания и реализации, его эффективность и скорость работы делают его одним из наиболее популярных алгоритмов сортировки.
Пример использования quicksort может быть следующим:
Предположим, у нас есть массив чисел: [7, 2, 9, 1, 6, 3]. Мы хотим упорядочить этот массив в порядке возрастания. Для этого мы можем использовать алгоритм quicksort:
Шаг 1: Выбираем опорный элемент. В данном случае мы можем выбрать любой элемент из массива, например, первый элемент - 7.
Шаг 2: Разделяем массив на две части: элементы, меньшие опорного элемента, и элементы, большие опорного элемента. В нашем примере получим [2, 1, 6, 3] и [9].
Шаг 3: Рекурсивно применяем алгоритм quicksort к каждой из двух частей массива.
Шаг 4: Соединяем отсортированные части массива вместе. В нашем примере получим [2, 1, 6, 3, 7, 9].
Таким образом, мы получаем отсортированный массив [1, 2, 3, 6, 7, 9].
Использование quicksort в практике позволяет эффективно и быстро сортировать массивы данных различных размеров. Этот алгоритм может быть применен в различных областях, таких как сортировка больших объемов данных, определение медианы или быстрое решение задачи поиска.
Преимущества и недостатки quicksort алгоритма
- Преимущества:
- QuickSort является одним из самых быстрых алгоритмов сортировки в большинстве случаев, особенно когда данные неупорядочены.
- Алгоритм QuickSort не требует дополнительной памяти для сортировки, кроме стека вызовов, что делает его эффективным с точки зрения использования памяти.
- QuickSort является адаптивным алгоритмом, что означает, что он может быстро реагировать на частично упорядоченные данные и выполнять сортировку в среднем случае за время O(n*logn).
- Алгоритм QuickSort легко реализовать и понять, и обычно не требует большого количества кода.
- Алгоритм QuickSort не является стабильным, что означает, что порядок элементов с одинаковыми значениями может быть изменен после сортировки.
- В худшем случае, когда массив уже отсортирован в порядке возрастания или убывания, алгоритм QuickSort имеет время выполнения O(n^2), что делает его медленным и менее эффективным в таких ситуациях.
- QuickSort требует рекурсивных вызовов, что может вызывать проблемы с использованием стека, особенно при сортировке больших массивов.
Несмотря на некоторые недостатки, QuickSort остается одним из самых популярных алгоритмов сортировки благодаря его эффективности и простоте реализации. Он широко используется в различных языках программирования и приложениях, и может быть оптимизирован для достижения лучшей производительности в конкретных случаях.
Рекомендации по выбору и оптимизации быстрой сортировки

- Выбор опорного элемента: Опорный элемент является центральной точкой алгоритма quicksort, поэтому его выбор имеет решающее значение для производительности. Желательно выбирать опорный элемент, который дает максимальную возможность сократить размеры подмассивов. Для этого можно использовать различные стратегии выбора опорного элемента, такие как выбор случайного элемента, выбор медианы из трех случайных элементов и т.д.
- Учет случаев наихудшего идеала: Quicksort имеет наихудший случай, когда массив уже отсортирован или содержит повторяющиеся элементы. В таких сценариях алгоритм может проявить себясвою максимальную эффективность. Для избегания этой проблемы можно использовать различные оптимизации, такие как случайная перестановка массива перед сортировкой или проверка элементов массива на предмет равенства перед разделением.
- Оптимизация рекурсивных вызовов: Quicksort является рекурсивным алгоритмом, поэтому оптимизация процесса рекурсивных вызовов может значительно улучшить производительность. Например, можно использовать хвостовую рекурсию или итеративную реализацию quicksort.
- Учет специфических особенностей массива: Quicksort может быть оптимизирован путем учета специфических характеристик массива, таких как наличие дубликатов или предсортированность. Например, для массивов с повторяющимися элементами можно использовать трехчастное разделение, чтобы избежать обработки одинаковых элементов. Для уже частично отсортированных массивов можно использовать алгоритмы, которые учитывают этот факт, например, "introsort".
- Оптимизация работы с памятью: Quicksort может иметь высокую потребность в памяти, особенно при больших массивах. Для улучшения производительности можно использовать различные техники оптимизации работы с памятью, такие как кэширование, использование индексов или специальных структур данных.
Правильный выбор и оптимизация быстрой сортировки могут значительно ускорить процесс сортировки и повысить общую производительность программы. Помни, что каждый конкретный случай может требовать индивидуального подхода к выбору оптимальных стратегий и техник.
Анализ статьи о quicksort: практическая ценность и полезность исследования

Статья, посвященная алгоритму сортировки quicksort, представляет собой ценный и полезный источник информации для программистов и разработчиков. В статье автор подробно объясняет принцип работы алгоритма, его преимущества и особенности применения.
Анализируя статью, можно отметить, что она основана на тщательно проведенном исследовании, которое включает в себя анализ времени выполнения и сложности алгоритма в различных сценариях. Автор предоставляет эмпирические данные, подтверждающие эффективность quicksort в сравнении с другими алгоритмами сортировки.
Статья содержит подробное описание каждого шага алгоритма и его механизма работы. Это позволяет программистам лучше понять суть алгоритма и его реализацию. В статье также представлены примеры кода на различных языках программирования, что делает ее еще более практической и полезной.
Автор статьи также обращает внимание на некоторые проблемы и ограничения quicksort, что помогает программистам избежать возможных ошибок при его использовании. Благодаря всестороннему анализу и объективному подходу, статья предлагает полную и достоверную информацию о quicksort.