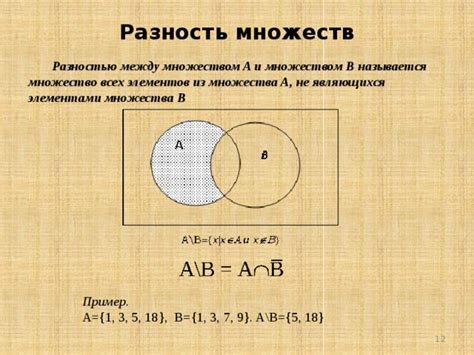
Разность множеств - это одно из основных понятий теории множеств, которое позволяет определить элементы, принадлежащие одному множеству, но не принадлежащие другому множеству. В математике это понятие активно используется при решении различных задач и проблем.
Особенностью разности множеств является то, что порядок операндов имеет значение. Разность множеств A и B обозначается как A \ B и определяется как множество всех элементов, принадлежащих множеству A, но не принадлежащих множеству B.
Примерно пустого множества в контексте разности множеств можно рассмотреть на примере двух множеств: A = {1, 2, 3} и B = {2, 4, 6}. В этом случае разность множеств A \ B будет определяться как множество {1, 3}, так как элементы 1 и 3 принадлежат множеству A, но не принадлежат множеству B.
Основные понятия и определения

Перед тем, как погрузиться в изучение разности множеств, полезно ознакомиться с некоторыми основными понятиями и определениями, связанными с темой.
| Множество | Неупорядоченная коллекция элементов без повторений. |
| Элемент множества | Конкретный объект или значение, принадлежащий множеству. |
| Пустое множество | Множество, не содержащее ни одного элемента. |
| Разность множеств | Множество, содержащее все элементы, принадлежащие первому множеству, но не принадлежащие второму множеству. |
| Обозначение разности множеств | Разность множеств A и B обозначается как A \ B или A - B. |
Ознакомление с этими понятиями поможет вам лучше понять сути и особенности разности множеств. В следующих разделах мы рассмотрим примеры пустого множества и его роли в операциях с множествами.
Особенности разности множеств
Особенностью операции разности множеств является то, что порядок множеств, участвующих в операции, имеет значение. Результат операции будет зависеть от порядка, в котором множества указаны.
Если A и B - два множества, то разность множеств обозначается как A \ B или A - B.
Результатом разности множеств будет новое множество, содержащее только те элементы, которые присутствуют в A, но отсутствуют в B.
Особенностью разности множеств является то, что порядок элементов в результирующем множестве может отличаться от порядка элементов в исходных множествах.
Примеры пустого множества

В различных областях знания пустые множества часто встречаются в качестве примеров и ситуаций.
В математике пустое множество является фундаментальным понятием. Например, если рассматривать множество всех натуральных чисел, которые меньше нуля, то получится пустое множество. Аналогично, если рассмотреть множество решений уравнения, которых не существует, получится также пустое множество.
В программировании пустые множества также имеют своё применение. Например, в языке Python можно создать пустое множество при помощи функции set() или использовать фигурные скобки {}.
Другим примером использования пустых множеств являются базы данных. Если в базе данных отсутствуют записи, то для представления такого состояния используется пустое множество.
И наконец, в повседневной жизни тоже можно встретить примеры пустых множеств. Например, пустое множество обуви в шкафу означает, что в шкафу нет ни одной пары обуви.