Результат деления чисел — как получить правильный ответ?

Деление является одной из важнейших операций в математике, позволяющей разделить одно число на другое. Однако, эту операцию не всегда возможно выполнить на "автомате". Все мы помним, как в школе учили правила деления - нужно указывать остаток, проверять правильность ответа и т.д. В данной статье мы рассмотрим правильные методы получения ответа при делении чисел, которые помогут нам избежать ошибок и получить точный результат.

Первым и самым простым методом является деление в столбик, который основан на раздельном делении цифр чисел. Для этого необходимо записать делимое и делитель в столбик и последовательно разделять их цифры. Затем умножаем получившиеся частичные результаты на соответствующие степени 10 и суммируем их.

Однако, при выполнении деления в столбик необходимо быть внимательными и следить за правильностью операций. Ошибки могут быть связаны как с некорректным построением столбиков и пропуском цифр, так и с неправильным перемещением запятой в десятичной дроби. Помимо этого, ответы, полученные при помощи деления в столбик, требуют дополнительной проверки и округления в зависимости от требований задачи.

Методы деления чисел: как правильно получить ответ

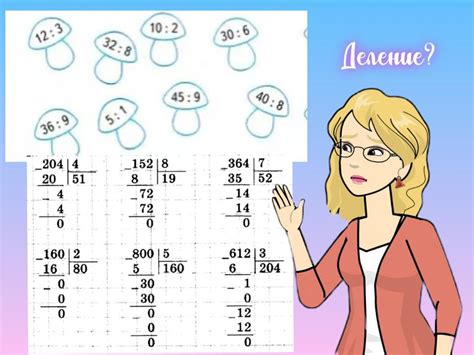
1. Деление в столбик:

Для выполнения деления в столбик, мы записываем делимое число сверху и делитель снизу, после чего начинаем делить цифру за цифрой. В случае, если в результате деления получается остаток, он записывается в столбик снизу и переносится на следующую цифру.

2. Деление в уме:

Деление в уме выполняется с помощью различных приемов: деление на основе умножения, рассмотрение особых случаев, использование знаний таблицы умножения и другие. Основная идея этого метода - сократить количество выполняемых действий, чтобы быть быстрее и эффективнее.

3. Деление с десятичной частью:

Иногда деление приводит к появлению десятичных чисел в частном. В этом случае, мы записываем диагональную черту после остатка, и продолжаем делить цифры после запятой, используя аналогичные методы как при делении в столбик. Деление чисел с десятичными частями требует большей внимательности и точности в выполнении.

Каждый из этих методов имеет свои достоинства и может использоваться в разных ситуациях. Важно умеренно тренироваться в каждом из методов, чтобы быть способным быстро и точно выполнять деление чисел.

Основные этапы деления чисел

1. Выбор чисел для деления. Необходимо определить делимое - число, которое будет делиться, и делитель - число, на которое будет происходить деление.
2. Подготовка чисел. Если числа имеют разное количество разрядов, необходимо выполнить выравнивание, добавив необходимое количество нулей к числу с меньшим количеством разрядов.
3. Первый шаг деления. В данном этапе необходимо вычесть делитель из делимого и записать полученную разность.
4. Повторение шага 3. После первого шага необходимо повторять вычитание делителя из полученной разности до тех пор, пока разность будет больше либо равна делителю.
5. Подведение итогов. После того, как разность станет меньше делителя, результатом деления является полученное значение разностью и остатком.

Основные этапы деления чисел позволяют получить правильный ответ и контролировать процесс деления. Применение этих методов гарантирует точность результата и помогает в решении различных задач, требующих деления чисел.

Выбор подходящего метода

При делении чисел существует несколько методов, которые можно использовать в зависимости от искомого результата и условий задачи. Ниже приведены основные подходы к выбору подходящего метода деления:

1. Деление в столбик. Этот метод наиболее распространен и прост в использовании. Он подходит для деления чисел любой сложности и позволяет получить точный результат.
2. Деление сокращением. Этот метод подходит для деления чисел, когда одно из чисел делится нацело на другое число. Он позволяет быстро получить результат без необходимости выполнять длинные вычисления.
3. Деление наибольшим разрядом. Этот метод подходит для деления чисел большой разрядности. Он позволяет упростить вычисления и получить приближенный результат.
4. Деление по модулю. Этот метод подходит для деления чисел, когда необходимо получить остаток от деления. Он позволяет быстро определить остаток без необходимости выполнять полное деление.

Выбор подходящего метода зависит от конкретной задачи и требуемой точности результата. Важно учитывать условия задачи и обращать внимание на особенности чисел, которые необходимо поделить.