Геометрия - наука, изучающая формы и структуры в пространстве. Конус - одна из наиболее интересных и сложных геометрических фигур. Его форма напоминает усеченный шар, у которого одна из сторон узкая и острая, а другая - широкая и выпуклая.
Для рисования и конструкции конуса существуют различные методы. Один из самых простых способов - использование циркуля и линейки. Необходимо выбрать центр будущего конуса и нарисовать окружность с заданным радиусом. Затем, с помощью линейки, провести диаметр, который будет служить основанием будущего конуса. Узкая сторона конуса получится путем соединения центра окружности с одним из концов диаметра.
Кроме того, существует метод построения конуса с использованием треугольника. Для этого необходимо на плоскости нарисовать треугольник заданных размеров. Затем, с помощью перпендикуляра, проведенного из одного из вершин треугольника к противоположной стороне, можно получить основание конуса. Остается только соединить вершину треугольника с конечной точкой перпендикуляра, и конус будет готов.
Рисование конуса в геометрии
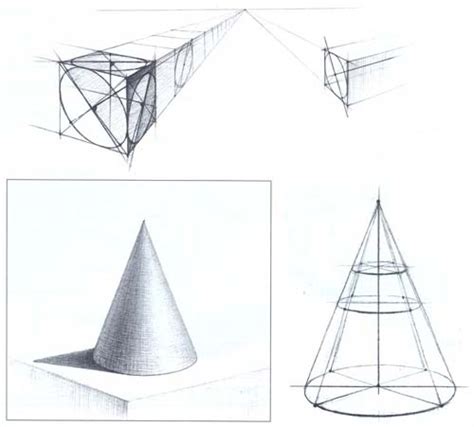
Один из способов нарисовать конус – это использовать таблицу. Ниже приведена таблица, которая позволяет поэтапно нарисовать конус:
| Основание | ||
| / | \ | |
| / | / | \ |
| * | * | * |
| Вершина |
В таблице используются символы "/" и "\", чтобы обозначить строительные линии, а символ "*" – для отметки точек. Поэтапно соединяя точки и линии, получается рисунок конуса.
Рисование конуса в геометрии – это один из интересных и полезных способов закрепить знания о данной геометрической фигуре. Такой метод дает возможность увидеть различные свойства и характеристики конуса, такие как высота, боковая поверхность, объем и другие.
Методы построения конуса
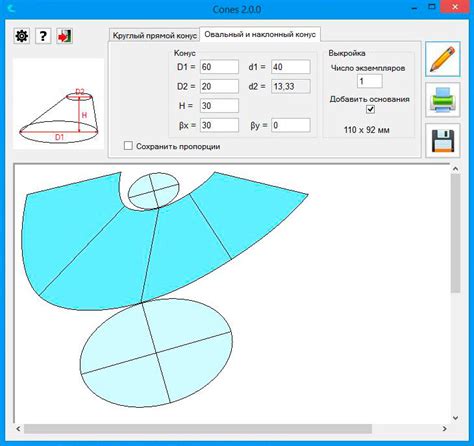
Первый метод построения конуса заключается в соединении прямой, называемой образующей, с соответствующими точками основания конуса. Для этого нужно взять точку на плоскости основания и провести прямую через эту точку и вершину конуса. Затем, повторяя данную операцию для всех точек основания, получим все наклонные грани конуса.
Второй метод состоит в использовании окружности основания и точки, называемой высотой конуса. Для построения конуса нужно взять основание - окружность, и из нее взять одну точку, называемую высотой конуса. Затем, соединив эту точку с каждой точкой окружности, получим все наклонные грани и вершину конуса.
Третий метод предлагает использовать два треугольника для построения конуса. Берем два равных треугольника, одним основание конуса, другим - его боковая поверхность. Затем, приклеиваем треугольник с боковой поверхностью по всей длине его стороны к соответствующей стороне треугольника, служащему основанием конуса. Получим конус с наклонными гранями.
Изучение и понимание данных методов позволят ученикам и студентам углубить свои знания в геометрии и развить навыки работы с пространственными фигурами.
Как нарисовать конус с помощью циркуля и линейки
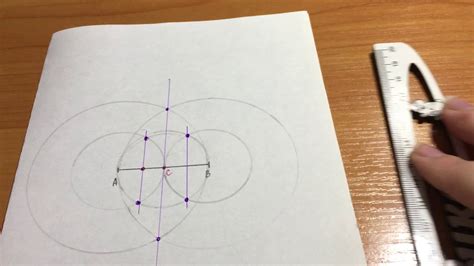
Чтобы нарисовать конус, вам понадобится лист бумаги, карандаш, циркуль и линейка. Следуйте следующим шагам:
Шаг 1:
Нарисуйте прямую линию, которая будет служить основанием вашего конуса. Она может быть горизонтальной или наклонной - в зависимости от того, как вы хотите настроить угол наклона вашего конуса.
Шаг 2:
На основании выбранной линии нарисуйте точку в центре. Эта точка будет являться вершиной вашего конуса.
Шаг 3:
Установите радиус циркуля так, чтобы он был равен одной из сторон основания вашего конуса, и отметьте на основании две точки - слева и справа от центральной точки. Эти две точки будут служить как сегменты периметра основания конуса.
Шаг 4:
Используя линейку, соедините точки периметра основания с вершиной конуса. Полученные линии будут образовывать боковую поверхность конуса.
Теперь, ваш конус нарисован! Вы можете использовать эти инструкции как отправную точку и настроить конус по своему усмотрению, изменяя углы и пропорции.
Рисование конуса - это занимательная и полезная практика, которая помогает изучить геометрию и развить навыки работы с циркулем и линейкой. Попробуйте создать разные размеры и формы конусов, экспериментируйте с их расположением и взаимодействием с другими геометрическими фигурами.
Рисование конуса с использованием геометрического набора
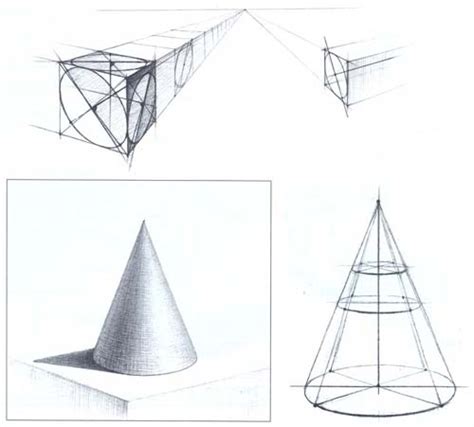
Сначала нарисуйте окружность на листе бумаги с помощью компаса. Она будет базовым основанием конуса. Затем из центра окружности проведите прямую линию, которая будет служить осью конуса. Длина этой линии должна соответствовать высоте конуса, которую вы выберете.
На оси конуса отметьте две точки: одну на расстоянии, равном радиусу окружности, а другую на расстоянии, равном сумме радиуса и высоты конуса. Соедините эти две точки прямой линией.
Теперь, с помощью геометрического набора, проведите дугу от радиуса окружности до прямой линии, соединяющей точки на оси. Эта дуга будет вторым основанием конуса.
Используя прямую линию, соединяющую точки на оси, и дугу, проведенную с помощью компаса, соедините соответствующие точки на окружности, получив боковую поверхность конуса.
Таким образом, вы сможете нарисовать конус с использованием геометрического набора. Этот инструмент позволяет визуализировать и конструировать геометрические фигуры, что является необходимым навыком в изучении геометрии.
Конус в геометрии: основные понятия

Основные элементы конуса:
- Высота: прямая линия, соединяющая вершину конуса с центром основания.
- Вершина: точка, в которой пересекаются образующие конуса.
- Радиус основания: расстояние от центра окружности, являющейся основанием, до любой ее точки.
- Образующая: линия, соединяющая вершину конуса с точками на окружности основания.
- Сектор конуса: фигура, ограниченная двумя радиусами основания и дугой окружности основания.
Конусы часто используются в математике, физике, инженерии и архитектуре. Изучение и понимание основных понятий конуса позволяет проводить сложные вычисления, строить модели и решать реальные проблемы в различных областях науки и техники.
Конус: формула для расчета площади поверхности

Для расчета площади поверхности конуса с радиусом основания R и образующей h можно использовать следующую формулу:
| Часть поверхности | Формула |
|---|---|
| Боковая поверхность | Площадь = π * R * l |
| Основание | Площадь = π * R^2 |
| Полная поверхность | Площадь = π * R * l + π * R^2 |
Где l - образующая конуса, которая соединяет вершину с центром основания, а π (пи) - математическая константа, примерное значение которой равно 3,14159.
Используя эти формулы, можно легко вычислить площадь поверхности конуса и получить точные результаты для различных значений радиуса и образующей.
Например, если радиус основания R равен 5 и образующая h равна 10, то площадь поверхности конуса будет равна:
Площадь = π * 5 * 10 + π * 5^2 = 157.08 + 78.54 ≈ 235.62
Таким образом, площадь поверхности конуса с данными значениями равна примерно 235.62 квадратных единиц.
Примеры задач по конусу в геометрии

Рассмотрим несколько задач, связанных с конусом:
Пример 1:
У рыбака есть треугольный конус, в основании которого сторона равна 10 см. Высота конуса составляет 15 см. Найдите объем и площадь поверхности этого конуса.
Решение:
Для вычисления объема конуса используется формула V = (1/3) * П * r^2 * h, где V – объем, П – число «пи», r – радиус основания, h – высота.
Подставим известные значения:
V = (1/3) * 3.14 * (5^2) * 15 = 392.5 см^3
Чтобы найти площадь поверхности можно использовать формулу S = П * r * (r + g), где S – площадь поверхности, g – образующая конуса.
Подставим значения:
S = 3.14 * 5 * (5 + 15) = 314 см^2
Таким образом, объем конуса равен 392.5 см^3, а площадь поверхности – 314 см^2.
Пример 2:
У вас есть деловые шляпы двух размеров: большая с высотой 20 см и радиусом основания 8 см, и маленькая с высотой 15 см и радиусом основания 6 см. Какую шляпу, была бы она цельной, можно было бы более компактно поместить в коробку с размерами сторон 20 см * 20 см * 20 см?
Решение:
Чтобы найти объем каждой шляпы, воспользуемся формулой V = (1/3) * П * r^2 * h.
Для большой шляпы:
V_1 = (1/3) * 3.14 * (8^2) * 20 ≈ 671 см^3
Для маленькой шляпы:
V_2 = (1/3) * 3.14 * (6^2) * 15 ≈ 565 см^3
Объем коробки составляет V_коробки = 20 * 20 * 20 = 8000 см^3.
Таким образом, можно было бы компактно поместить маленькую шляпу в коробку, так как её объем меньше объема коробки.
Роль конуса в естественных и технических объектах

1. Естественные объекты:
- Вулканы: многие вулканы образуются в результате извержения магмы из глубин земли. Форма вулкана очень похожа на конус, и это связано с тем, что магма вытекает из вулкана по центральному отверстию и образует характерную узкую коническую вершину.
- Сосульки: сосульки образуются при низких температурах, когда вода замерзает в капельках и начинает накапливаться постепенно. Капли падают и собираются на кончике, создавая длинные, конические структуры.
- Раковины улиток: улитки строят свои раковины в форме спирали, которая схожа с формой конуса. Это позволяет им защититься от внешних угроз и обеспечить место для жизни.
2. Технические конструкции:
- Дорожные конусы: конусы яркого цвета используются для обозначения различных областей дороги, например, для разделения движения при ремонте или регулирования трафика в определенных зонах.
- Устройство дно скважин: при бурении скважин для различных целей, например, для добычи нефти или воды, конусы используются для создания стержней, которые поддерживают стенки скважины и предотвращают обрушение земли.
- Конусы для диффузоров и усилителей звука: в акустике конусы используются для создания диффузоров и усилителей звука. Конусный дизайн позволяет распространить звуковые волны и усилить звуковое давление.
Это лишь некоторые примеры, демонстрирующие роль конуса в различных естественных и технических объектах. Благодаря своей уникальной форме и свойствам, конус является важным элементом в разных областях и используется как в природе, так и в человеческой деятельности.