Руководство по нахождению вершин отрезков по известным серединам

Поиск вершин отрезков является важной задачей во многих областях математики, физики и компьютерных наук. Эта задача возникает, когда требуется найти точки, соответствующие определенным значениям или условиям, в заданной последовательности. Но что делать, если известны только середины отрезков? В этом руководстве мы рассмотрим эффективный алгоритм, который позволяет найти вершины отрезков по известным серединам.

В основе этого алгоритма лежит идея использования симметричных свойств отрезков. Рассмотрим отрезок AB, будем считать его середину M. Для нахождения вершин отрезка мы можем использовать следующую формулу: A = 2M - B. Данная формула позволяет нам найти одну вершину отрезка, зная только его середину и другую вершину.

Применение этого алгоритма может быть особенно полезным в задачах, связанных с графиками функций, определением координат точек на плоскости или в трехмерном пространстве, а также в алгоритмах компьютерного зрения, обработке изображений и многочисленных других областях. Знание данного алгоритма позволит вам эффективно решать множество сложных задач в своей работе или учебе.

Важность поиска вершин отрезков

Когда речь идет о поиске вершин отрезков, главная задача заключается в определении границ каждого отрезка. Знание координат вершин позволяет строить различные геометрические фигуры и выполнять математические операции над ними. Например, нахождение расстояния между двумя точками или определение пересечения отрезков.

Кроме того, правильный поиск вершин очень важен при визуализации геометрических данных. Например, в программировании часто требуется отобразить отрезки на экране с помощью компьютерной графики. Точное определение вершин отрезков позволяет корректно отображать их на экране и создавать реалистичные и точные изображения.

Из-за важности правильного поиска вершин отрезков, существует множество алгоритмов и методов для его выполнения. Некоторые из них являются достаточно простыми и прямолинейными, в то время как другие требуют более сложных вычислений и аналитических методов. Все эти методы направлены на достижение максимальной точности и надежности при поиске вершин отрезков.

Как найти вершины отрезков

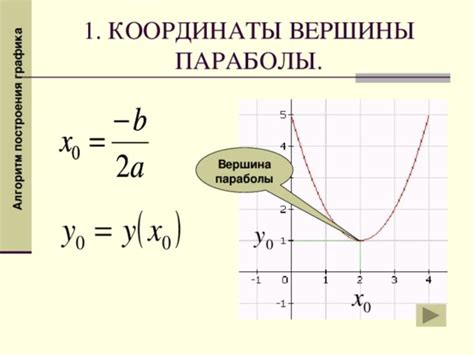
При работе с геометрическими фигурами, в том числе и с отрезками, часто возникает необходимость в определении координат их вершин. В данной статье мы рассмотрим несколько способов нахождения вершин отрезков по известным серединам.

1. Использование формулы координат точки на отрезке

   Для нахождения вершин отрезка по известным координатам его середины, можно воспользоваться формулой:

   • Координата X вершины A равна дважды координате X середины минус координаты X вершины B.
   • Координата Y вершины A равна дважды координате Y середины минус координаты Y вершины B.
   • Координаты вершины B равны симметричным относительно середины отрезка координатам вершины A.

2. Использование геометрической конструкции

   Для нахождения вершин отрезка можно построить прямую, проходящую через середину отрезка, и пересекающую его. Пересечение этой прямой с самим отрезком даст нам вершины A и B.

   • Для этого необходимо определить коэффициенты уравнения прямой, проходящей через середину отрезка. Затем, решив систему уравнений прямой и отрезка, найдем точки пересечения.

Выбор способа нахождения вершин отрезков зависит от конкретной задачи и доступных инструментов. Однако, независимо от выбранного подхода, важно правильно определять координаты середин отрезков для получения точных результатов.

Использование геометрических вычислений

Геометрические вычисления оказываются весьма полезными при поиске вершин отрезков по известным серединам. Они позволяют определить координаты вершин отрезков в двумерном пространстве с помощью геометрических свойств и формул.

Один из наиболее распространенных методов использования геометрических вычислений для поиска вершин отрезков - это определение координат вершин посредством вычисления расстояния между известной серединой и одной из вершин отрезка. Для этого используется формула расстояния между двумя точками в декартовой системе координат.

Другим методом является использование геометрического построения. При заданных известных серединах отрезков можно построить треугольники, в которых вершинами служат середины, а одна из сторон - искомые вершины отрезков. Такой подход основан на геометрическом свойстве прямоугольного треугольника и позволяет найти координаты вершин без необходимости в вычислениях.

Геометрические вычисления важны при работе с графиками и визуализацией данных. Они помогают определить положение объектов в пространстве, а также строить и анализировать различные геометрические фигуры. Использование геометрических вычислений в поиске вершин отрезков значительно упрощает процесс и обеспечивает точность результатов.

Применение метода половинного деления

Для применения метода половинного деления необходимо иметь начальное приближение для искомой вершины отрезка и предельное значение точности. Алгоритм заключается в следующем:

Шаг 1: Задаем начальное приближение для вершины отрезка. Это может быть середина отрезка или любая другая точка.

Шаг 2: Разделяем отрезок пополам, вычисляя значение функции в серединной точке.

Шаг 3: Сравниваем значение функции в серединной точке с известной серединой отрезка. Если они совпадают с нужной точностью или удовлетворяют условию задачи, то алгоритм завершается. В противном случае переходим к шагу 4.

Шаг 4: Выбираем новый отрезок для дальнейших итераций. Если значение функции в серединной точке меньше известной середины отрезка, то новый отрезок будет содержать левую часть, иначе - правую часть. Возвращаемся к шагу 2.

Метод половинного деления позволяет находить вершины отрезков с высокой точностью и скоростью. Он широко применяется в различных областях, включая численное решение уравнений, оптимизацию функций и аппроксимацию данных.

Середины отрезков и их роль в поиске вершин

Когда известны середины отрезков, можно использовать их для определения исходных координат вершин. Для этого необходимо знание длин отрезков и центральных точек.

С помощью середин отрезков можно определить, где начинаются и заканчиваются вершины. Путем сравнения координат середин с исходными значениями можно вычислить их положение и определить, находится ли вершина на левой или правой половине отрезка.

Середины отрезков также позволяют найти точки пересечения и сегменты, симметричные относительно друг друга. Путем нахождения середин отрезков и сравнения их координат можно определить, где происходит пересечение и какие сегменты являются симметричными.

Важно отметить, что для использования середин отрезков в поиске вершин необходима информация о длинах отрезков и их координатах. Без этих данных невозможно определить положение исходных точек на отрезке. Поэтому, предварительное измерение и запись данных об отрезках являются важным шагом в процессе поиска вершин.

Определение и значимость середин отрезков

Знание середин отрезков имеет большое значение в геометрии и других областях. Оно позволяет находить другие важные точки и сегменты отрезка, а также применять их в различных вычислениях. Середины отрезков используются в множестве геометрических задач, а также в картографии, рисовании и компьютерной графике.

Например, зная середину отрезка, можно находить другие точки на нем, такие как концы, пересечения с другими отрезками или окружностями. Они также используются для нахождения центра или радиуса окружности, описанной вокруг отрезка.

Середины отрезков часто используются в конструкциях и алгоритмах, связанных с геометрией. Например, они могут быть использованы для построения сегментов биссектрисы треугольника или для определения центра масс системы точек, заданных отрезками.

Таким образом, определение середин отрезков имеет важное значение в геометрии и других областях, и их знание позволяет решать различные задачи, связанные с отрезками и их свойствами.

Алгоритм поиска вершин отрезков по известным серединам

Для эффективного поиска вершин отрезков по известным серединам существует следующий алгоритм:

1. Создать пустой список для хранения вершин отрезков.
2. Для каждой из известных середин отрезков:
   • Найти все возможные пары точек, для которых середина отрезка будет равна известной середине.
   • Добавить найденные вершины отрезков в список.
3. Отсортировать список вершин отрезков в порядке возрастания по координате x.

Таким образом, данный алгоритм позволяет найти вершины отрезков по известным серединам и упорядочить их по координате x.

Пример:

• Известные середины отрезков: 2, 5, 8
• Найденные вершины отрезков: (1, 3), (4, 6), (7, 9)
• Отсортированные вершины отрезков: (1, 3), (4, 6), (7, 9)

Таким образом, после выполнения алгоритма, мы получим список вершин отрезков, полностью определенных по известным серединам и упорядоченных по координате x.

Шаг 1: Вычисление длины отрезков

Для вычисления длины отрезков, необходимо знать координаты начальной и конечной точек каждого отрезка. Формула расчета длины отрезка выглядит следующим образом:

Длина отрезка = Корень квадратный из ((x₂ - x₁)² + (y₂ - y₁)²)

где:

• x₁ и y₁ – координаты начальной точки отрезка;
• x₂ и y₂ – координаты конечной точки отрезка.

После применения этой формулы, получаем длину каждого отрезка. Длина измеряется в единицах, подходящих для конкретной задачи или системы координат.

Вычисление длины отрезков является важным шагом, поскольку она позволяет нам провести дальнейшие расчеты, а также определить вершины отрезков по известным серединам.

Обратите внимание, что для применения данной формулы необходимо точно знать координаты начала и конца каждого отрезка. В противном случае, результат может быть неточным или некорректным.

Шаг 2: Определение координат вершин отрезков

1. Найдите середину отрезка, используя известные координаты вершин.
2. Определите координаты одной из вершин отрезка как сумму координат середины и половины длины отрезка по каждой оси.
3. Вычислите координаты другой вершины отрезка, вычитая половину длины отрезка из координат середины по каждой оси.

Повторите эти шаги для каждого отрезка, используя известные координаты середин и длины отрезков.

Пример:

Отрезок AB:
- Середина: (x1, y1)
- Длина: L1
Координата вершины A:
- xA = x1 + L1/2
- yA = y1 + L1/2
Координата вершины B:
- xB = x1 - L1/2
- yB = y1 - L1/2

Повторите этот пример для каждого отрезка, заменяя значения переменных x1, y1 и L1 на соответствующие значения середины и длины отрезков.

Теперь вы знаете, как определить координаты вершин отрезков с использованием информации о серединах и длинах. Эта информация будет полезна при поиске и визуализации отрезков на плоскости.