Определение типа экстремума в функции является важной задачей в математическом анализе. Знание типа экстремума позволяет оптимизировать функцию и найти ее наибольшие или наименьшие значения. Одним из методов определения типа экстремума является использование гессиана, который позволяет проанализировать кривизну функции.
Введение гессиана дает возможность найти точки перегиба, минимумы и максимумы функции. Гессиан - это симметричная матрица, состоящая из вторых производных функции. Он позволяет определить ориентацию и форму эллиптических, гиперболических или параболических экстремумов. Для этого используются постоянные границы.
Определение типа экстремума гессе осуществляется по знаку определителя гессиана. Если он положительный, то экстремум является параболическим и минимумом. Если определитель отрицательный, это указывает на параболический максимум. Нулевой определитель указывает на гиперболический экстремум.
Что такое экстремум и зачем он нужен?

Зачем нужно определять экстремум? Это позволяет нам найти наилучшие решения или состояния системы. Например, в экономике экстремум функции спроса и предложения позволяет определить оптимальные цены и количество товаров на рынке. В физике экстремумы функций энергии и потенциала позволяют найти устойчивые состояния системы.
Определение типа экстремума гессе является важным инструментом для более точного анализа экстремумов. Гессиан - это матрица, составленная из вторых производных функции. Анализ типа экстремума позволяет определить, является ли точка экстремумом и в каком направлении происходит изменение функции в окрестности этой точки. Это помогает нам лучше понять поведение функций и принимать обоснованные решения.
Когда применяют метод Гессе?

Основными преимуществами метода Гессе являются:
- Точность: метод Гессе позволяет достичь высокой точности при нахождении экстремума функции.
- Скорость: благодаря использованию информации о вторых производных, метод Гессе может обладать высокой скоростью сходимости.
- Универсальность: метод Гессе может быть применен к любой многомерной функции, не зависимо от ее формы и структуры.
Однако, следует учитывать, что метод Гессе также имеет некоторые ограничения:
- Сложность вычислений: для применения метода Гессе требуется вычисление и хранение вторых частных производных функции, что может быть сложным и затратным процессом.
- Проблемы сингулярности: в некоторых случаях матрица Гессе может быть сингулярной или плохо обусловленной, что приводит к неустойчивости метода.
- Возможность застревания в локальных экстремумах: метод Гессе не гарантирует нахождение глобального экстремума и может застрять в локальных экстремумах.
В целом, метод Гессе является мощным инструментом для нахождения экстремума многомерной функции, который может быть применен в различных областях, включая оптимизацию, экономику, физику, машинное обучение и другие.
Применение метода Гессе требует достаточных знаний и навыков в математике и численных методах, а также осторожности при выборе параметров и интерпретации результатов. Важно учитывать особенности конкретной задачи и обстоятельства, чтобы правильно применять метод Гессе и достичь желаемых результатов.
Основные принципы определения типа экстремума гессе
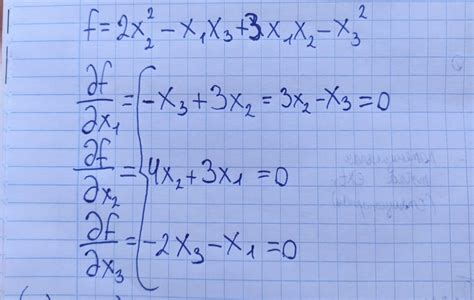
Гессиан является квадратной матрицей, элементы которой представляют собой вторые производные функции по каждой переменной.
Основные принципы определения типа экстремума гессе:
- Если все собственные значения гессиана положительны, то функция имеет локальный минимум. В этом случае, функция выпукла вниз и имеет точку минимума.
- Если все собственные значения гессиана отрицательны, то функция имеет локальный максимум. В этом случае, функция выпукла вверх и имеет точку максимума.
- Если собственные значения гессиана имеют как положительные, так и отрицательные значения, то функция имеет седловую точку. В этом случае, функция выпукла в одном направлении и вогнута в другом.
- Если гессиан не является положительно-определённым или отрицательно-определённым, то тип экстремума не определён методом Гессе. В этом случае, требуется использовать другие методы для определения типа экстремума функции.
Определение типа экстремума гессе позволяет выявить основные характеристики функции и помогает в понимании её поведения около точек экстремума.
Шаги по определению типа экстремума гессе

Для определения типа экстремума гессе следует выполнить ряд шагов:
1. Вычислить гессиан функции. Гессиан представляет собой матрицу вторых производных функции по ее переменным. Значения элементов матрицы гессиана позволяют оценить поведение функции в окрестности точки экстремума.
2. Вычислить определитель гессиана. Определитель гессиана является важным показателем, позволяющим определить тип экстремума. Если определитель гессиана положителен, то это указывает на то, что точка является локальным минимумом. Если определитель гессиана отрицателен, то это указывает на наличие локального максимума. Если определитель гессиана равен нулю, то тип экстремума не определен.
3. Вычислить след гессиана. След гессиана также является важным показателем при определении типа экстремума. Если след гессиана положителен, то это указывает на наличие выпуклого минимума. Если след гессиана отрицателен, то указывает на наличие вогнутого максимума. Если след гессиана равен нулю, то тип экстремума не определен.
4. Анализировать результаты. Исходя из полученных значений определителя и следа гессиана, можно определить тип экстремума. Если оба значения отрицательны, то это указывает на наличие вогнутого максимума. Если оба значения положительны, то это указывает на наличие выпуклого минимума. Если одно из значений положительно, а другое отрицательно, то это указывает на точку седловины или точку перегиба. Если оба значения равны нулю, то тип экстремума не определен.
5. Проверить условия. После определения типа экстремума гессе следует проверить выполнение условий, которые могут указывать на наличие точки экстремума. В некоторых случаях может потребоваться использование дополнительных методов, например, метода первых производных или метода наименьших квадратов.
Примеры применения метода Гессе для определения типа экстремума
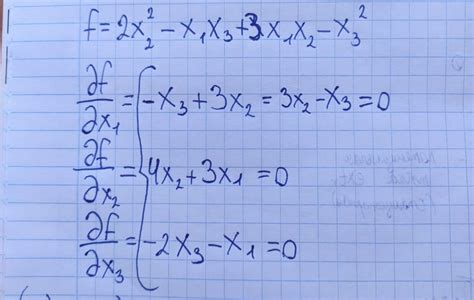
Давайте рассмотрим примеры применения метода Гессе для определения типа экстремума.
Пример 1:
Пусть у нас есть функция f(x, y) = x2 + 2y2. Чтобы найти точки экстремума, мы должны вычислить гессиан:
H = [[2, 0], [0, 4]].
Так как все элементы гессиана положительны, это означает, что у нас есть локальный минимум в точке (0, 0).
Пример 2:
Рассмотрим функцию f(x, y) = x3 - 3xy + y3. Вычислим гессиан:
H = [[6x - 6y, -3], [-3, -6x + 6y]].
Чтобы определить тип экстремума, мы должны рассмотреть значения гессиана в окрестности точки. Для точки (0, 0) имеем:
H = [[0, -3], [-3, 0]].
Так как определители подматриц равны нулю, гессиан не может определить тип экстремума в этой точке. В таких случаях необходимо использовать другие методы для анализа функции.
Пример 3:
Рассмотрим функцию f(x, y) = x4 - 6x2y2 + y4. Вычислим гессиан:
H = [[12x2 - 12y2, -24xy], [-24xy, -12x2 + 12y2]].
Проверим типы экстремума для нескольких точек:
- Для точки (0, 0): гессиан равен H = [[0, 0], [0, 0]]. Это означает, что тип экстремума не определен.
- Для точки (1, 1): гессиан равен H = [[-24, -24], [-24, -24]]. Так как определители подматриц ненулевые и одного знака, это означает, что у нас есть седловая точка.
- Для точек (1, -1) и (-1, 1): гессиан также равен H = [[-24, 24], [24, -24]]. Так как определители подматриц ненулевые и противоположного знака, это означает, что у нас есть локальный максимум и локальный минимум соответственно.
Как видно из примеров, метод Гессе является мощным инструментом для определения типа экстремума функции. Он позволяет находить локальные минимумы, максимумы и седловые точки, что может быть полезно при анализе и оптимизации функций в различных областях науки и промышленности.
1. Анализ диагональных элементов матрицы Гессе:
Если все диагональные элементы матрицы Гессе положительны, то точка является минимумом. Если все диагональные элементы отрицательны, то точка является максимумом. Если же существуют как положительные, так и отрицательные элементы, то тип экстремума следует определять с использованием вторых производных.
2. Анализ недиагональных элементов матрицы Гессе:
Недиагональные элементы матрицы Гессе отражают взаимное влияние между переменными. Если есть сильное взаимодействие между переменными, то пересчет типа экстремума может потребовать дополнительных подходов и методов.
3. Дополнительные методы анализа:
В случае, когда анализ диагональных и недиагональных элементов не дает однозначного решения, следует применить другие методы, такие как методы первых производных, методы определения знака функции, методы градиента и т. д. Это позволит получить более точные и надежные результаты.
4. Проверка точности вычислений: