Функция e - одна из основных математических функций, играющая важную роль в различных областях науки, техники и финансов. Ее производная имеет особое значение, что позволяет решать различные задачи, связанные с изменением величин.
Производная функции показывает, как быстро меняется значение функции при изменении аргумента. Для функции e ее производная имеет простую формулу и часто используется в решении задач, связанных с процессами экспоненциального роста или убывания.
Нахождение производной функции e происходит по определению производной, используя граничное значение предела при стремлении разности значений функции к нулю. Процесс нахождения производной основан на применении базовых правил дифференцирования и требует некоторых навыков и знаний математики.
Определение производной функции e и ее значение
Производная функции e может быть найдена с использованием дифференциального исчисления. Для этого применяется правило дифференцирования экспоненты, которое гласит: если у функции e^x берется производная, то она остается неизменной.
Таким образом, производная функции e равна самой себе, то есть (d/dx)e^x = e^x. Это правило дифференцирования экспоненты является одним из основных и широко используется при решении дифференциальных уравнений и других математических задач.
Значение функции e, также известное как число Эйлера, приближенно равно 2.71828. Оно играет важную роль в различных областях науки и инженерии, включая физику, статистику, экономику и многое другое. В математических формулах и уравнениях часто встречается функция e, что свидетельствует о ее важности и широком применении.
Что такое производная функции e

Производная функции e обозначается как e', и она вычисляется по определенному алгоритму. Для нахождения производной функции e нужно использовать теорию дифференцирования, которая является частью математического анализа.
Производная функции e может использоваться для решения различных задач, например, в физике, экономике или статистике. Она позволяет определить изменение функции e в зависимости от изменения некоторого параметра.
Знание производной функции e может быть полезно при решении задач оптимизации, поиска экстремумов функции или аппроксимации данных. Она также позволяет более точно оценить поведение функции e вблизи определенной точки.
Формула вычисления производной функции e
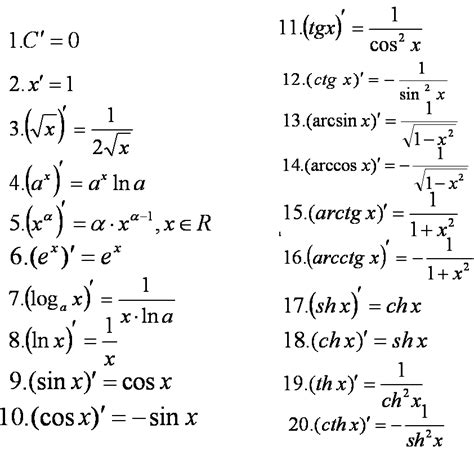
Для вычисления производной функции e необходимо использовать следующую формулу:
| Функция | Производная |
| ex | ex |
В данной формуле x является независимой переменной, по которой берется производная. Найденное значение будет точкой на кривой графика функции e.
Пример:
Дано: f(x) = ex
Требуется найти производную функции f(x).
Решение:
Используем формулу: f'(x) = ex
Таким образом, производная функции e равна самой функции ex. Это означает, что функция e возрастает со скоростью, равной ее текущему значению.
Пример вычисления производной функции e

Чтобы вычислить производную этой функции, воспользуемся определением производной:
- Найдем предел отношения изменения функции к изменению переменной при стремлении изменения переменной к нулю.
- Для функции ex это можно записать следующим образом:
d(ex) = limh→0 [(ex+h - ex)/h]
- Раскроем скобки и упростим выражение:
d(ex) = limh→0 [ex * ((eh - 1)/h)]
- При h→0, выражение (eh - 1)/h стремится к 1:
d(ex) = limh→0 [ex * 1]
- Таким образом, производная функции ex равна ex.
В итоге, d(ex)/dx = ex.
Таким образом, производная функции e равна самой функции, что делает ее особенно полезной при решении математических задач.
Значение производной функции e в различных точках
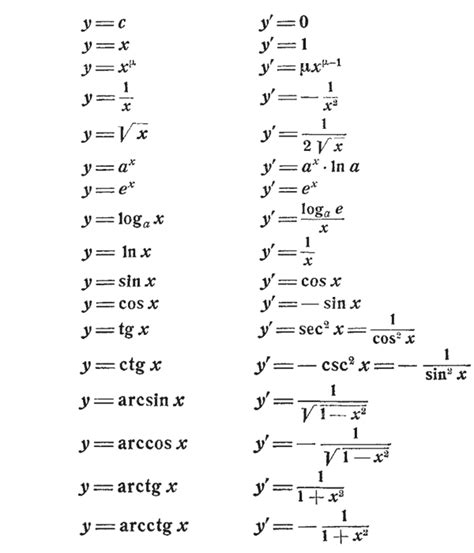
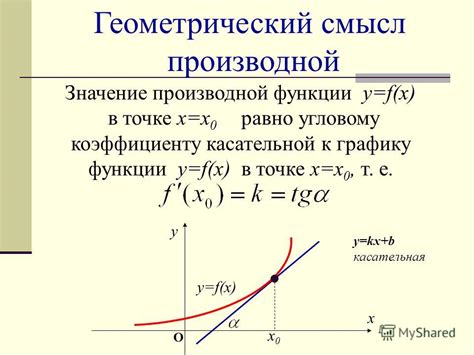
Значение производной функции e может быть определено в любой точке на оси действительных чисел. Но существует особое значение, которое является основной особенностью функции e: производная функции e в любой точке равна самой функции e.
Математически это записывается как:
e'(x) = e^x
Таким образом, производная функции e равна ее значению при любом значении x. Например, при x = 0 производная функции e равна e^0 = 1, а при любом другом значении x она равна e в этой точке.
Также стоит отметить, что производная функции e не зависит от выбора основания логарифма или других параметров. Она всегда равна самой функции e.
График производной функции e и его особенности
Во-первых, график производной функции e является постоянной и равной самой функции e. Это означает, что независимо от значения x, производная функции e всегда равна самой функции. Таким образом, угол наклона графика производной функции e всегда будет равен 1. Это часто называют свойством самоподобия или "самостоятельности" функции e.
Во-вторых, график производной функции e является положительным и монотонно возрастающим на всей числовой прямой. Это означает, что производная функции e всегда положительна и ее значение увеличивается по мере увеличения x. Таким образом, график производной функции e будет продолжаться вверх и вправо без каких-либо изменений.
В-третьих, график производной функции e пересекает ось абсцисс в точке (0, 0). Это означает, что производная функции e имеет нулевое значение в точке x = 0. Это свойство также отражает "самостоятельность" функции e и является одним из ключевых свойств производной функции e.
Важно отметить:
График производной функции e является непрерывным и гладким, не имеет скачков, точек разрыва или углов. Это свойство делает производную функции e особенно полезной в анализе и моделировании различных явлений и процессов в науке, физике, экономике и других областях.
График производной функции e также помогает иллюстрировать связь между оригинальной функцией e и ее изменением с течением времени или других переменных. Он позволяет определить скорость изменения функции e в каждой точке и понять ее поведение.
Изучение графика производной функции e и его особенностей играет важную роль в понимании основ математического анализа и приложений функции e в различных областях знаний.