Рекурсия - это мощный инструмент в программировании, позволяющий решать задачи, которые могут быть описаны в виде повторяющихся шагов или подзадач.
В Python рекурсия реализуется с использованием функций, которые вызывают сами себя. В этом учебнике мы рассмотрим принцип работы рекурсии и покажем несколько примеров, чтобы помочь вам лучше понять, как использовать эту концепцию в своих программах.
Перед тем, как продолжить, давайте сначала разберемся, что такое рекурсия.
Рекурсия - это процесс, в котором функция вызывает саму себя внутри своего тела. Эта концепция может быть трудной для понимания, но когда вы осознаете, как она работает, вы сможете использовать ее для создания элегантных решений для сложных задач.
Определение и принцип работы рекурсии

Принцип работы рекурсии заключается в следующем: функция вызывает саму себя для решения подзадачи, продолжая вызывать себя до тех пор, пока не будет достигнуто базовое условие - условие выхода из рекурсии. Когда базовое условие достигнуто, функция начинает возвращать результаты выполнения отложенных вызовов функции, снизу вверх, объединяя их и возвращая ответ на исходную проблему.
Основная идея рекурсии заключается в разделении задачи на более простые подзадачи и решении каждой из них с использованием тех же шагов, что и оригинальная задача. Таким образом, рекурсивный алгоритм сводит решение сложной задачи к решению более простых задач, что делает его мощным инструментом для решения сложных проблем.
Однако, при использовании рекурсии необходимо быть осторожным, чтобы избежать бесконечной рекурсии. Бесконечная рекурсия может возникнуть, если не указано базовое условие выхода из рекурсии.
Несмотря на потенциальные сложности, правильно примененная рекурсия является одним из мощных инструментов программирования, позволяющим писать элегантный и компактный код для решения различных задач.
Зачем нужна рекурсия в Python?

Основная идея рекурсии заключается в том, чтобы функция вызывала сама себя. Это позволяет разделить сложную задачу на более простые подзадачи, которые решаются тем же самым алгоритмом. Рекурсивный алгоритм может разложить задачу на несколько уровней глубины, решая каждую подзадачу отдельно и комбинируя результаты в конечный результат. Таким образом, рекурсия позволяет снизить сложность задачи и упростить код.
Одним из основных преимуществ рекурсии является ее элегантность. Рекурсивный алгоритм может быть гораздо проще и понятнее, чем эквивалентный итеративный алгоритм. Кроме того, рекурсия позволяет повысить переиспользуемость кода, так как функция может вызываться повторно с разными аргументами.
Однако, использование рекурсии также имеет некоторые недостатки. Рекурсивные функции могут потреблять больше памяти и быть менее эффективными, чем итеративные алгоритмы. Также, некорректное использование рекурсии может привести к бесконечному циклу и вызвать исключение "рекурсивную глубину превышена". Поэтому, при использовании рекурсии необходимо быть осторожным и учитывать возможные ограничения.
Основные понятия рекурсии

Одной из основных характеристик рекурсивной функции является базовый случай. Базовый случай определяет, когда функция должна прекратить свою работу и вернуть результат. Если базовый случай не определен, функция будет вызываться бесконечное число раз, что приведет к ошибке "переполнения стека".
Кроме базового случая, рекурсивные функции также имеют рекурсивный случай или случаи. Рекурсивный случай определяет, когда функция должна вызвать саму себя для решения подзадачи. Это позволяет функции повторно использовать свой код для обработки разных случаев.
При использовании рекурсии необходимо следить за тем, чтобы рекурсивные вызовы прогрессивно приближались к базовому случаю. В противном случае функция может "зациклиться" и не завершиться.
Рекурсия может быть очень полезной для решения некоторых задач, в том числе вычислений факториала, нахождения чисел Фибоначчи, обхода деревьев и графов и многих других. Однако, из-за использования стека вызовов, рекурсия может потреблять больше памяти и быть менее эффективной по сравнению с итеративным решением.
Важно понимать, что рекурсия - это необходимый, но не всегда единственный способ решения задачи. Иногда итеративное решение может быть более простым и эффективным.
Рекурсивные функции

Рекурсивные функции представляют собой способ решения задачи путем вызова самой себя. Этот подход основан на принципе разделения задачи на более простые подзадачи, которые решаются аналогичным образом.
Рекурсия в Python работает по следующему принципу: если условие выхода из функции не выполнено, функция вызывает саму себя с измененными параметрами. Такой процесс продолжается до тех пор, пока условие выхода не будет достигнуто.
Пример рекурсивной функции может быть функция вычисления факториала числа. Факториал числа n (обозначается n!) представляет собой произведение всех натуральных чисел от 1 до n включительно. Формально можно определить факториал следующим образом:
n! = 1 * 2 * 3 * ... * (n-1) * n
Для вычисления факториала можно использовать рекурсивную функцию, которая будет вызываться с уменьшенным значением n до достижения условия выхода из рекурсии. Например, рекурсивная функция factorial() может быть определена следующим образом:
# Рекурсивная функция для вычисления факториала числа
def factorial(n):
if n == 0:
return 1
return n * factorial(n-1)
В данном примере, если значение n равно 0, функция возвращает 1 - это основание рекурсии. В противном случае, функция возвращает произведение значения n на результат вызова функции самой себя с аргументом n-1. Такое поведение позволяет достичь условия выхода при n = 0 и последовательно умножить все числа от 1 до n включительно на следующее число.
Рекурсивные функции обычно организуются по принципу "разделяй и властвуй", то есть задача разбивается на более простые подзадачи, которые решаются рекурсивно, а затем результаты комбинируются для получения окончательного результата.
Однако, при написании рекурсивных функций необходимо учитывать возможность переполнения стека вызовов, особенно для больших значений аргументов. Использование более эффективных алгоритмов, например, итеративного подхода или динамического программирования, может быть предпочтительнее в некоторых случаях.
Базовый случай и рекуррентное соотношение

Базовый случай - это условие, при котором рекурсивная функция прекращает вызывать саму себя и возвращает конкретное значение. Базовый случай является своеобразной остановкой рекурсивного процесса, чтобы избежать бесконечной рекурсии. Это обычно связано с достижением определенного условия или обработкой самых простых случаев, когда рекурсия не требуется.
Рекуррентное соотношение - это математическое выражение, которое определяет отношение между более крупной задачей и меньшими подзадачами. В контексте рекурсии, рекуррентное соотношение определяет, как рекурсивная функция вызывает саму себя с уменьшенными параметрами, чтобы решить более маленькую подзадачу. Каждая итерация рекурсии приближает нас к базовому случаю, путем решения все более простых подзадач в каждой рекурсивной итерации.
Точное определение базового случая и рекуррентного соотношения зависит от конкретной задачи, которую вы пытаетесь решить с помощью рекурсии. Правильное определение базового случая и рекуррентного соотношения являются ключевыми факторами для успешной работы с рекурсией.
Например, при решении задачи вычисления факториала числа, базовый случай будет определен как факториал числа 0 или 1, которые равны 1. Рекуррентное соотношение будет определено как умножение числа на факториал предыдущего числа. Таким образом, рекурсивная функция будет вызывать саму себя с уменьшенным числом в качестве аргумента, до достижения базового случая.
| Число | Факториал |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
Использование базовых случаев и рекуррентного соотношения позволяет элегантно решать задачи с помощью рекурсии. Однако важно помнить, что неправильно определенные базовые случаи или неверно сформулированное рекуррентное соотношение могут привести к непредсказуемым результатам или бесконечной рекурсии. Поэтому, при работе с рекурсией всегда стоит внимательно анализировать задачу и проверять корректность базового случая и рекуррентного соотношения.
Примеры рекурсии в Python

Факториал числа
Факториал числа n (обозначается n!) - это произведение всех положительных целых чисел от 1 до n. Рекурсивная функция для вычисления факториала может быть определена следующим образом:
def factorial(n): if n == 0: return 1 else: return n * factorial(n-1)В данном примере функция factorial вызывает саму себя, уменьшая значение аргумента на 1 до тех пор, пока не достигнет базового случая, когда n равно 0. Функция возвращает 1 в этом случае и продолжает умножать n на результат рекурсивного вызова factorial(n-1).
Сумма элементов списка
Рекурсивная функция для вычисления суммы элементов списка может быть определена следующим образом:
def list_sum(lst): if len(lst) == 0: return 0 else: return lst[0] + list_sum(lst[1:])В данном примере функция list_sum вызывает саму себя, передавая в качестве аргумента срез списка lst, исключая его первый элемент. Функция продолжает вызывать себя, пока список не опустеет до базового случая, когда его длина становится равной 0. Затем функция возвращает 0 в этом случае и продолжает складывать первый элемент списка с результатом рекурсивного вызова list_sum для оставшейся части списка.
Быстрое возведение в степень
Рекурсивная функция для быстрого возведения числа в степень может быть определена следующим образом:
def power(base, exponent): if exponent == 0: return 1 else: return base * power(base, exponent - 1)В данном примере функция power вызывает саму себя, уменьшая значение аргумента exponent на 1 до тех пор, пока не достигнет базового случая, когда exponent равно 0. Функция возвращает 1 в этом случае и продолжает умножать base на результат рекурсивного вызова power с уменьшенным значением exponent.
Это всего лишь некоторые примеры рекурсивных функций в Python. Рекурсия может быть использована для решения широкого спектра задач, и для каждой задачи необходимо определить базовый случай и правила для рекурсивного вызова функции.
Вычисление факториала
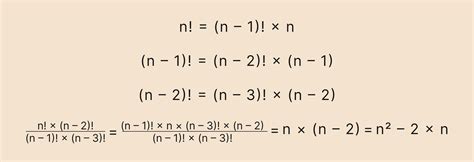
Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа.
Пример вычисления факториала:
- Если число равно 0 или 1, то его факториал равен 1.
- Иначе, умножаем число на факториал предыдущего числа.
В Python вычисление факториала можно реализовать с помощью рекурсии:
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n-1)
Пример использования функции:
result = factorial(5)
Вычисление факториала с помощью рекурсии основано на принципе разбиения задачи на более простые подзадачи. Функция вызывает саму себя с уменьшенным значением аргумента до достижения базового случая (когда аргумент равен 0 или 1). Каждый раз при вызове функции создается новый стек вызовов, что может привести к использованию большого объема памяти при вычислении факториала большого числа.
Вычисление чисел Фибоначчи
В Python можно реализовать вычисление чисел Фибоначчи с помощью рекурсивной функции. Рекурсивная функция - это функция, которая вызывает сама себя.
Ниже приведен пример рекурсивной функции для вычисления чисел Фибоначчи:
def fibonacci(n):
if n В этом примере функция fibonacci(n) вызывает сама себя дважды. Если значение аргумента n меньше или равно 1, функция возвращает само значение n. В противном случае, функция возвращает сумму двух вызовов функции fibonacci(n-1) и fibonacci(n-2).
Введите номер числа Фибоначчи: 6
Число Фибоначчи с номером 6 равно 8Использование рекурсии для вычисления чисел Фибоначчи позволяет лаконично реализовать алгоритм, но может привести к повторному вычислению одних и тех же значений, что замедляет работу программы. Для улучшения производительности можно использовать мемоизацию - запоминание уже вычисленных значений и их повторное использование во время работы программы.
Преимущества и недостатки рекурсии

Преимущества рекурсии:
- Простота и понятность кода: рекурсивные функции часто оказываются более компактными и легкими для понимания, чем их итеративные аналоги.
- Универсальность: рекурсия позволяет решать сложные задачи, которые трудно или невозможно решить итерациями.
- Гибкость: рекурсия позволяет легко изменять и расширять функциональность, добавлять новые возможности и условия.
Недостатки рекурсии:
- Потребление ресурсов: использование рекурсии может приводить к большому потреблению памяти и процессорного времени.
- Возможность зацикливания: неправильно организованная рекурсия может привести к бесконечному циклу вызовов функций и зависанию программы.
- Сложность отладки: отладка рекурсивного кода может быть сложной задачей из-за большого количества рекурсивных вызовов и вложенности.
При использовании рекурсии необходимо учитывать эти преимущества и недостатки, чтобы эффективно решать задачи и избегать возможных проблем.