Сортировка является одним из основных алгоритмических приемов в программировании. Сортировка позволяет упорядочить данные по определенному критерию и улучшить производительность работы программы. В зависимости от конкретной задачи и объема данных, выбор эффективного метода сортировки играет важную роль в оптимизации программного кода.
Существует множество алгоритмов сортировки, каждый из которых имеет свои сильные и слабые стороны. Один из самых простых и популярных методов сортировки – это пузырьковая сортировка. В основе этого алгоритма лежит последовательное сравнение пар элементов, при котором меняются местами элементы с наименьшим значением. Пузырьковая сортировка проста в реализации, но при больших объемах данных ее эффективность существенно снижается.
Для работы с большими объемами данных рекомендуется использовать более эффективные алгоритмы сортировки, такие как сортировка слиянием или быстрая сортировка. Сортировка слиянием основана на принципе «разделяй и властвуй», при котором массив данных разделяется на две половины, затем каждая половина сортируется отдельно, а затем объединяется в один упорядоченный массив. Этот алгоритм позволяет выполнять сортировку с большой эффективностью, но требует дополнительного использования памяти для временных массивов.
Разные алгоритмы сортировки

Алгоритм сортировки пузырьком:
Один из простейших алгоритмов сортировки – сортировка пузырьком. Он получил свое название из-за способа сравнения элементов: больший элемент "всплывает" вверх, как пузырек, опускаясь на свое место.
Алгоритм сортировки выбором:
Алгоритм сортировки выбором основан на выборе наименьшего элемента и перемещении его в начало массива. Процесс повторяется до тех пор, пока все элементы не будут отсортированы.
Алгоритм сортировки вставками:
Алгоритм сортировки вставками основан на последовательном включении каждого элемента в уже упорядоченную часть массива. Элементы, которые больше текущего значения, сдвигаются вправо, пока не будет найдено правильное место для вставки.
Алгоритм сортировки слиянием:
Алгоритм сортировки слиянием основан на принципе разделяй и властвуй. Массив разделяется на две равные части, затем каждая половина сортируется отдельно, после чего они объединяются в одну упорядоченную последовательность.
Алгоритм быстрой сортировки:
Алгоритм быстрой сортировки – это рекурсивный алгоритм, который основан на выборе опорного элемента и разбиении массива на две части. Затем происходит рекурсивная сортировка этих двух частей. Он работает очень быстро на большинстве случаев, но может потребовать много памяти в худшем случае.
Алгоритм сортировки подсчетом:
Алгоритм сортировки подсчетом работает для целых чисел. Он создает дополнительный массив, который используется для подсчета количества вхождений каждого числа. Затем полученные значения исходного массива собираются в правильном порядке.
Сортировка пузырьком
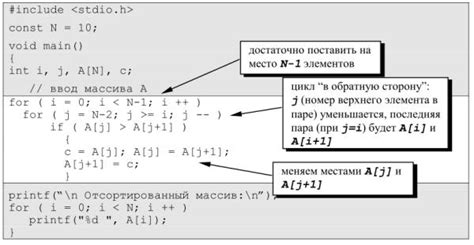
Алгоритм сортировки пузырьком можно представить следующим образом:
- Проходим по всему массиву и сравниваем каждый элемент с его соседними.
- Если элемент больше следующего, то меняем их местами.
- Повторяем шаги 1 и 2 до тех пор, пока не пройдем по всему массиву без необходимости выполнения обмена.
Сортировка пузырьком имеет квадратичную сложность, то есть ее время выполнения в худшем случае составляет O(n^2), где n - количество элементов в массиве. Однако, алгоритм прост в понимании и реализации, поэтому может быть использован для небольших объемов данных или в учебных целях.
Пример реализации сортировки пузырьком на языке JavaScript:
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len; i++) {
for (var j = 0; j < len - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
var temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}Данный код совершает проходы по массиву и меняет местами соседние элементы, если необходимо, до тех пор, пока массив не будет отсортирован. Результатом работы функции будет отсортированный массив.
Хотя сортировка пузырьком не является эффективным алгоритмом для больших объемов данных, она способствует более глубокому пониманию работы сортировки и может быть полезна при изучении основ программирования.
Сортировка вставками
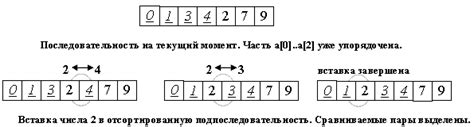
Сортировка вставками является простым и эффективным алгоритмом сортировки для небольших массивов или уже частично отсортированных массивов. Она имеет временную сложность O(n^2), что делает ее неэффективной для больших массивов с большим количеством элементов. Однако для случаев, когда понятность кода и легкость реализации имеют большое значение, сортировка вставками может быть отличным выбором.
Алгоритм сортировки вставками можно реализовать на множестве популярных языков программирования, таких как C++, Java, Python и других. Он может быть использован для сортировки массивов чисел, строк и других типов данных. Сортировка вставками может быть также стабильной сортировкой, сохраняя исходный порядок элементов с одинаковыми значениями.
Быстрая сортировка
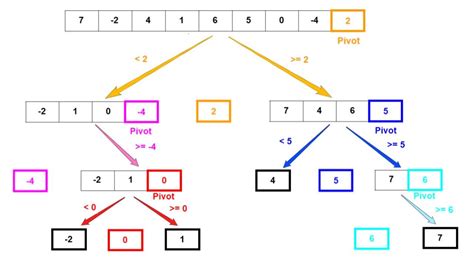
Алгоритм быстрой сортировки состоит из следующих шагов:
- Выбрать опорный элемент из массива данных.
- Разделить массив на две части: слева от опорного элемента должны находиться все элементы, меньшие либо равные опорному, а справа - все элементы, большие опорного.
- Рекурсивно применить алгоритм быстрой сортировки к обеим частям массива.
- Объединить отсортированные части массива.
В результате выполнения этих шагов мы получим отсортированный массив данных.
Преимущества быстрой сортировки заключаются в высокой скорости работы и использовании меньшего количества памяти. Она является универсальной и может быть применена к различным типам данных.
Важным моментом при использовании быстрой сортировки является правильный выбор опорного элемента. От этого выбора зависит скорость работы алгоритма. Часто в качестве опорного элемента выбирают середину массива.
Несмотря на свою эффективность, быстрая сортировка может иметь худший случай работы O(n^2) в том случае, если массив уже отсортирован по возрастанию или убыванию. Однако, на практике такие случаи редко встречаются и быстрая сортировка обычно работает очень быстро.
Сортировка слиянием

Алгоритм сортировки слиянием состоит из следующих шагов:
- Рекурсивно разделить исходный массив на две равные части, пока не останется массив из одного элемента.
- Отсортировать получившиеся две части рекурсивно, используя тот же алгоритм сортировки слиянием.
- Соединить две отсортированные части в один отсортированный массив.
Преимущества сортировки слиянием:
- Стабильность: алгоритм сохраняет порядок сортировки для равных элементов.
- О(n log n) время выполнения: эффективный алгоритм для сортировки больших наборов данных.
- Не требует значительных затрат по памяти: использует только дополнительный массив для хранения промежуточных данных.
Недостатки сортировки слиянием:
- Низкая эффективность при работе с малыми наборами данных, из-за необходимости деления массива на части.
- Требует дополнительной памяти для временного хранения промежуточных данных.
Сортировка слиянием применяется во многих областях, где требуется сортировка больших объемов данных, включая базы данных, анализ данных, компьютерные графики и многие другие.
Сортировка выбором

Процесс сортировки выбором можно разделить на две части:
1. На каждой итерации прохода по массиву выбирается наименьший элемент из неотсортированной части и помещается в начало этой части.
2. Таким образом, на каждой итерации размер неотсортированной части уменьшается на 1, а отсортированная часть увеличивается на 1.
Алгоритм сортировки выбором имеет сложность O(n^2), где n – количество элементов в массиве.
Применение данного алгоритма целесообразно для маленьких массивов или когда уже есть представление о положении наименьшего (или наибольшего) элемента в массиве.