Синус - одна из основных тригонометрических функций, которая находит свое широкое применение в различных областях науки и техники. Но как найти значение синуса для треугольника без использования сложных формул и таблиц? Существует простой способ, который можно использовать для нахождения синуса треугольника без особых математических навыков.
Для начала, рассмотрим прямоугольный треугольник. Возьмем сторону, противолежащую прямому углу, и обозначим ее как противоположную, а соседнюю сторону - как прилежащую. Тогда отношение длины противоположной стороны к длине прилежащей стороны будет равно синусу угла противолежащего этим сторонам.
Применяя этот принцип к треугольникам произвольной формы, можно использовать отношение высоты треугольника к длине основания, чтобы найти синус угла, образованного этими сторонами. Таким образом, для нахождения синуса треугольника достаточно знать его высоту и длину основания.
Этот простой способ нахождения синуса треугольника особенно удобен, когда нет возможности использовать сложные математические выкладки или таблицы синусов. Он позволяет быстро и точно определить значение синуса треугольника с минимальными усилиями.
Что такое синус треугольника?
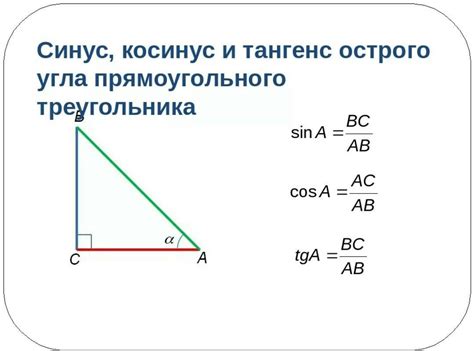
Другими словами, синус треугольника - это отношение длины противолежащей стороны к длине гипотенузы треугольника. Обозначается символом sin и выражается в виде отношения длины сторон:
sin(угол) = длина противолежащей стороны / длина гипотенузы.
Синус имеет значения в диапазоне от -1 до 1. Значение равное -1 соответствует прямому углу (90 градусов), значение равное 0 - углу в 0 градусов или 180 градусов (синус равен 0 для угла прямой или полной окружности), и значение равное 1 - углу в 90 или 270 градусов (синус равен 1 для углов прямой или полной окружности).
| Угол | Синус |
|---|---|
| 0 градусов | 0 |
| 30 градусов | 0.5 |
| 45 градусов | 0.707 |
| 60 градусов | 0.866 |
| 90 градусов | 1 |
Знание синуса треугольника может быть полезно при решении различных задач в геометрии, физике, а также в других областях наук и инженерии. Оно позволяет нам определить длины сторон и углы треугольника, а также решать задачи связанные с треугольными отношениями.
Формула для вычисления синуса треугольника
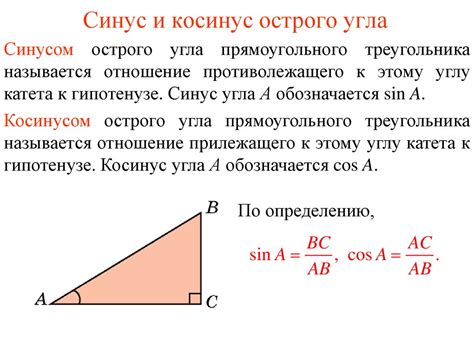
Формула для вычисления синуса треугольника выглядит следующим образом:
sin(A) = a / c
где:
sin(A) - синус угла A;
a - длина противоположной углу A стороны;
c - длина гипотенузы треугольника.
Данная формула основана на соотношениях, которые справедливы для прямоугольного треугольника. Синус угла A равен отношению длины противоположной стороны A к длине гипотенузы.
Используя эту формулу, можно легко вычислить синус треугольника и использовать полученные значения в дальнейших расчетах или анализе геометрических свойств треугольника.
Применение синуса треугольника в геометрии

Синус треугольника определяется отношением длины противолежащего катета к гипотенузе. Благодаря этому определению, мы можем находить длины сторон и углы в треугольнике без необходимости измерений. Синус треугольника также может быть использован для нахождения площади треугольника, если известны две его стороны и угол между ними.
Применение синуса треугольника находит свое применение не только в геометрии, но и в других научных и технических областях. Например, синус треугольника используется при решении задач связанных с архитектурой, строительством, навигацией и многими другими отраслями. Знание синусов позволяет ученым и инженерам более точно моделировать и предсказывать поведение сложных конструкций и природных явлений.
Таким образом, понимание и применение синуса треугольника играют важную роль в науке и технике в целом. Это дает нам возможность более эффективно работать с геометрическими объектами и решать различные задачи, связанные с треугольниками и углами.
Примеры задач с использованием синуса треугольника
| Пример | Задача | Решение |
|---|---|---|
| Пример 1 | Найти длину стороны треугольника, если известны две другие стороны и угол между ними. | Используя формулу синуса треугольника: a / sin(A) = b / sin(B) = c / sin(C), где a, b и c - стороны треугольника, A, B и C - соответствующие углы, можно найти длину третьей стороны. Зная значения двух сторон и угла между ними, можно подставить значения в формулу и найти третью сторону треугольника. |
| Пример 2 | Найти значения углов треугольника, если известны длины всех его сторон. | Используя формулу синуса треугольника: sin(A) = a / c, sin(B) = b / c, sin(C) = c / c = 1, где a, b и c - стороны треугольника, A, B и C - соответствующие углы, можно найти значения углов треугольника. Зная значения всех сторон треугольника, можно найти соответствующие значения синусов с помощью этих формул и затем из них вычислить значения углов. |
| Пример 3 | Найти площадь треугольника, если известны длины двух его сторон и угол между ними. | Используя формулу площади треугольника: S = (1/2) * a * b * sin(C), где a и b - стороны треугольника, C - угол между ними, можно найти площадь треугольника. Зная значения двух сторон и угла между ними, можно подставить значения в формулу и найти площадь треугольника. |
Это лишь небольшой пример применения синуса треугольника в решении задач. В геометрии существует множество других задач, в которых можно использовать этот математический инструмент.