Геометрия является одним из ключевых предметов, которые необходимо сдать на ОГЭ. Этот предмет требует от учеников хорошего знания основных понятий и правил. Важно знать, как геометрия применяется в повседневной жизни и как она связана с другими науками.
На экзамене по геометрии учащимся предлагается решить несколько задач, которые позволяют проверить уровень их знаний и навыков работы с геометрическими фигурами. Есть определенный список тем, которые включены в программу ОГЭ по геометрии. Разберемся подробнее, какие именно темы нужно изучить и чему необходимо уделить особое внимание во время подготовки к ОГЭ.
В программе ОГЭ по геометрии включены следующие темы:
- Понятия о точке, прямой, отрезке, угле.
- Сравнение отрезков по длине.
- Сравнение углов по величине.
- Понятия о равных фигурах, подобных фигурах.
- Понятия об элементах параллельных, пересекающихся прямых.
- Построение фигур по заданным условиям.
- Периметр и площадь прямоугольника, треугольника, параллелограмма.
- Периметр и площадь круга.
- Объем и площадь поверхности прямоугольного параллелепипеда.
- Углы при пересечении прямых и параллельных прямых с плоскостями.
Ученикам необходимо усвоить эти темы и научиться решать задачи, связанные с ними. Кроме того, очень важно понимать, какие формулы и правила можно применить при решении определенной задачи. Тщательная подготовка к экзамену и систематическое повторение материала помогут ученикам успешно сдать ОГЭ по геометрии.
Основы геометрии - формулы, аксиомы, определения
Основные понятия и определения:
- Точка - элементарный объект без размеров и формы, обозначается заглавной буквой латинского алфавита (A, B, C).
- Прямая - бесконечно тонкая линия, которая располагается между двумя точками и не имеет ширины и конечной длины, обозначается строчной буквой латинского алфавита или двумя точками, через которые она проходит (a, b, AB).
- Отрезок - часть прямой между двумя точками, имеющая конечную длину, обозначается двумя точками (AB).
Формулы и свойства:
- Формула расстояния между двумя точками: AB = √((x2 - x1)2 + (y2 - y1)2), где A(x1, y1) и B(x2, y2) - координаты точек на плоскости.
- Формула площади прямоугольника: S = a * b, где a и b - стороны прямоугольника.
- Формула площади треугольника по координатам его вершин: S = 0.5 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|.
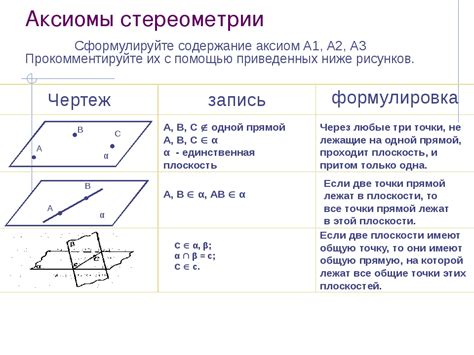
Аксиомы геометрии:
- Аксиома 1. Через любые две точки можно провести прямую.
- Аксиома 2. Любые две прямые либо пересекаются в одной точке, либо не пересекаются совсем.
- Аксиома 3. Через любую точку, не принадлежащую прямой, можно провести только одну прямую, параллельную данной.
Усвоение этих формул, определений и аксиом позволит вам успешно сдать экзамен по геометрии на ОГЭ.
Линии и углы - параллельные, перпендикулярные, смежные

Перпендикулярные линии - это две линии, которые пересекаются и образуют прямой угол, то есть угол в 90 градусов.
Смежные углы - это углы, которые имеют общую сторону и вершину. Сумма смежных углов равна 180 градусов.
Изучение свойств и особенностей линий и углов поможет разобраться во многих геометрических задачах и заданиях на экзамене по геометрии ОГЭ.
Равенство и подобие фигур - задачи на вычисление сторон и углов
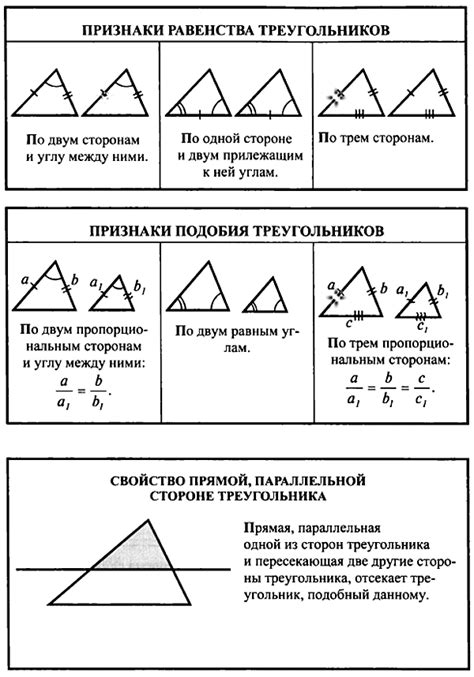
Одним из основных способов доказать равенство двух фигур является равенство всех их сторон и углов. В задачах на вычисление сторон фигур обычно требуется найти значения неизвестных сторон, используя заданные условия и известные свойства фигур.
Например, рассмотрим задачу: "В прямоугольном треугольнике ABC с гипотенузой AC известны значения угла B и стороны AB. Найдите значения сторон BC и AC". Для решения этой задачи необходимо использовать тригонометрический подход – применить теорему Пифагора и формулу синуса или косинуса для нахождения значений сторон BC и AC.
Задачи на вычисление углов фигур требуют нахождения неизвестных углов, исходя из заданных условий и известных свойств фигур. Например, рассмотрим задачу: "В параллелограмме ABCD угол A равен 60°. Найдите значения углов B, C и D". Для решения этой задачи нужно использовать свойства параллелограмма, в частности, то, что противоположные углы равны, и поэтому углы B, C и D также равны 60° каждый.
Также на экзамене по геометрии могут встретиться задачи на определение подобия фигур. Подобие фигур – это свойство, когда одна фигура получается из другой путем одновременного увеличения или уменьшения всех ее размеров. Задачи на определение подобия фигур могут требовать вычисления соотношений сторон и углов.
Например, рассмотрим задачу: "В прямоугольном треугольнике ABC с гипотенузой AC известны значения угла B и стороны AB. Найдите соотношения сторон треугольников ABC и A'В'С', если треугольник A'В'С' является подобным треугольнику ABC". Для решения этой задачи нужно применять свойства подобных треугольников и использовать соответствующие соотношения сторон и углов.
| Тема | Описание |
|---|---|
| Равенство фигур | Равенство всех сторон и углов двух фигур |
| Вычисление сторон | Нахождение значений неизвестных сторон фигур |
| Вычисление углов | Нахождение значений неизвестных углов фигур |
| Подобие фигур | Свойство одна фигура получается из другой путем одновременного увеличения или уменьшения всех ее размеров |
Треугольники и их свойства - медианы, высоты, биссектрисы
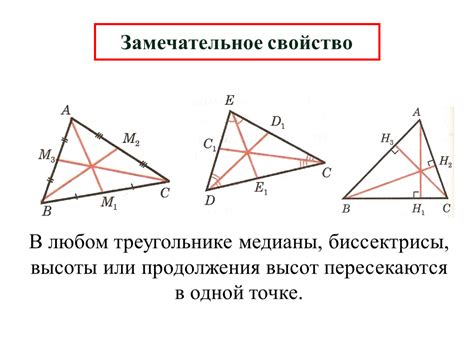
В геометрии существует несколько важных понятий, связанных с треугольниками, таких как медианы, высоты и биссектрисы.
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для любого треугольника существуют три медианы, которые пересекаются в одной точке - центре тяжести треугольника. Центр тяжести является точкой пересечения медиан и делит каждую медиану в отношении 2:1.
Высота треугольника - это отрезок, проведенный из вершины перпендикулярно противолежащей стороне. Для любого треугольника существует три высоты, которые могут пересекаться в одной точке - ортоцентре треугольника. Ортоцентр лежит внутри или на продолжении одной из сторон треугольника.
Биссектриса треугольника - это отрезок, который делит угол на две равные части. Для каждого угла треугольника существует одна биссектриса. Три биссектрисы треугольника могут пересекаться в одной точке - центре вписанной окружности треугольника.
Треугольники, их медианы, высоты и биссектрисы являются важными объектами изучения в геометрии. Изучение свойств этих объектов позволяет нам лучше понять геометрические закономерности и решать различные задачи.
| Название | Описание |
|---|---|
| Медиана | Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. |
| Высота | Отрезок, проведенный из вершины перпендикулярно противолежащей стороне. |
| Биссектриса | Отрезок, который делит угол на две равные части. |
Прямоугольники, квадраты и ромбы - периметр, площадь, диагонали
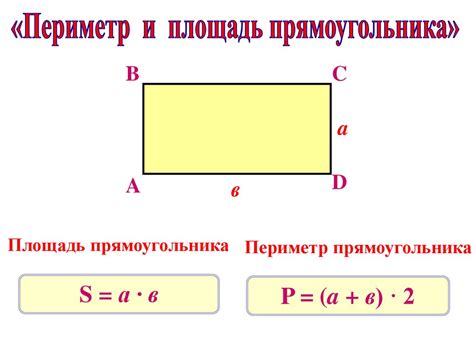
Геометрия представляет широкий спектр фигур, включая прямоугольники, квадраты и ромбы. Эти фигуры имеют свои уникальные свойства, которые позволяют рассчитывать их периметр, площадь и диагонали.
Прямоугольник - это четырехугольник, у которого все углы прямые. У прямоугольника есть две пары параллельных сторон. Для прямоугольника периметр рассчитывается по формуле P = 2a + 2b, где a и b - длины сторон. Площадь прямоугольника равна S = a * b, где a и b - длины сторон. Диагонали прямоугольника равны по длине и рассчитываются по теореме Пифагора: d = √(a^2 + b^2), где a и b - длины сторон.
Квадрат - это частный случай прямоугольника, у которого все стороны равны. У квадрата все углы прямые и все стороны равны друг другу. Для квадрата периметр рассчитывается по формуле P = 4a, где a - длина стороны. Площадь квадрата равна S = a^2, где a - длина стороны. Диагонали квадрата равны по длине и рассчитываются по теореме Пифагора: d = a√2, где a - длина стороны.
Ромб - это четырехугольник, у которого все стороны равны. У ромба все углы не прямые. Для ромба периметр рассчитывается по формуле P = 4a, где a - длина стороны. Площадь ромба равна S = h * a, где h - высота, опущенная на основание, a - длина основания. Диагонали ромба пересекаются под прямым углом и рассчитываются по теореме Пифагора: d1 = √(a^2 + b^2), d2 = √(c^2 + d^2), где a, b, c, d - длины сторон.
Параллелограммы и трапеции - основные свойства, формулы

У параллелограмма есть следующие свойства:
- Противоположные углы параллелограмма равны.
- Сумма углов параллелограмма равна 360 градусов.
- Диагонали параллелограмма делятся пополам и пересекаются в точке, которая является серединой каждой диагонали.
- Площадь параллелограмма равна произведению длин одной его стороны на высоту, опущенную на эту сторону.
Трапеция - это четырехугольник, у которого две противоположные стороны параллельны, а две другие стороны - нет.
У трапеции есть следующие свойства:
- Один из углов трапеции равен прямому углу 90 градусов.
- Сумма углов трапеции равна 360 градусов.
- Сумма длин оснований трапеции равна произведению полусуммы оснований на высоту.
- Площадь трапеции равна произведению полусуммы оснований на высоту.
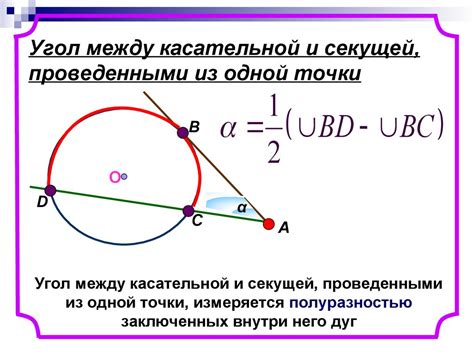
Окружности и дуги - центр, радиус, длина дуги, угол между касательной и хордой
Дуга – это часть окружности, состоящая из всех точек окружности, лежащих между двумя данными точками окружности. Дуга может быть измерена с помощью угла в радианах или величины дуги – длины части окружности, измеряемой в единицах длины, например, в сантиметрах.
Длина дуги может быть вычислена с помощью формулы:
длина дуги = 2πr(α/360),
где r - радиус окружности, α - величина угла дуги в градусах.
Угол между касательной и хордой - это угол, образованный между касательной к окружности в заданной точке и отрезком, соединяющим эту точку с другой точкой на окружности. Угол между касательной и хордой равен половине угла, опирающегося на эту дугу.
Исходя из формулы для длины дуги окружности, можно вывести формулу для угла между касательной и хордой:
α = 360(l/r),
где l - длина хорды, соединяющей две точки окружности, r - радиус окружности.
Эти понятия и формулы являются основными в геометрии окружностей и используются для решения задач на ОГЭ.
Планиметрия - задачи на комбинирование разных фигур

На ОГЭ по геометрии могут встретиться задачи, которые требуют понимания и умения комбинировать различные геометрические фигуры. Такие задачи могут представлять собой комбинации пересекающихся фигур, объединения двух или более фигур, нахождения площади или периметра составной фигуры.
Решение таких задач обычно требует знания основных свойств фигур, а также навыков разбиения сложных фигур на более простые элементы. При решении задачи на комбинирование фигур важно внимательно читать условие задачи, выделять ключевые данные и правильно интерпретировать их. Здесь также пригодятся навыки работы с формулами площади и периметра различных фигур.
Часто задачи на комбинирование фигур включают в себя такие фигуры, как прямоугольники, квадраты, треугольники, окружности и полуокружности. Знание их свойств и формул поможет более эффективно решать такие задачи.
Например, задачей на комбинирование фигур может быть нахождение площади фигуры, образованной двумя пересекающимися квадратами, или нахождение периметра фигуры, состоящей из прямоугольника и полуокружности.
Решая такие задачи, следует быть внимательным и аккуратным, чтобы не допустить ошибок в вычислениях и решении. Важно также уметь организовать свою работу и разбивать сложные задачи на последовательность более простых шагов.