Циркуль – это инструмент, который широко использовался в математике и геометрии на протяжении многих лет. С его помощью можно создавать различные геометрические фигуры, в том числе и девятиугольник. Девятиугольник представляет собой фигуру с девятью сторонами и девятью углами, и его создание требует некоторых навыков и инструментов.
Для того чтобы создать девятиугольник с помощью циркуля, вам понадобятся лист бумаги, карандаш, линейка и циркуль. Следуйте инструкциям ниже, чтобы успешно создать эту уникальную геометрическую фигуру.
- Возьмите лист бумаги и нарисуйте на нем отрезок любой длины. Этот отрезок будет служить одной из сторон вашего девятиугольника.
- Выберите любую точку на этом отрезке и отложите радиус вашего циркуля от нее.
- Сделайте пометку в этой точке, а затем используйте циркуль, чтобы провести окружность с заданным радиусом.
- Теперь выберите другую точку на первоначальном отрезке и проведите вторую окружность таким же образом, чтобы она пересеклась с предыдущей окружностью.
- Продолжайте этот процесс, выбирая новые точки на предыдущих отрезках и проводя окружности, пока не получите на бумаге восемь точек, образующих девятиугольник.
- Соедините полученные точки линиями, чтобы получить изображение девятиугольника. Уберите лишние линии и пометки, чтобы облегчить чтение и понимание фигуры.
Теперь у вас есть девятиугольник, созданный с помощью циркуля. Вы можете использовать эту технику для создания различных геометрических фигур и развития своих навыков в области математики и геометрии.
Циркуль и его возможности
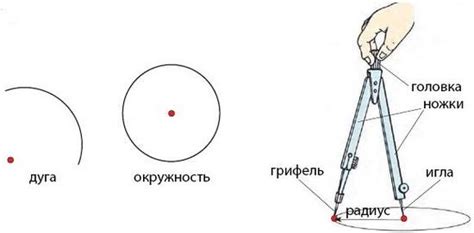
Циркуль имеет много полезных свойств и возможностей:
| 1. Создание окружностей | Циркуль позволяет легко и точно создавать окружности разных диаметров. Для этого нужно задать нужный радиус на масштабе циркуля и затем, прикладывая его к поверхности, провести карандаш или острие по окружности. |
| 2. Измерение расстояний | Циркуль может использоваться для измерения расстояния между двумя точками на плоскости. Для этого нужно установить карандаш в одну точку, а острие циркуля в другую, и затем измерить расстояние между ними на масштабе циркуля. |
| 3. Создание правильных фигур | С помощью циркуля можно создавать правильные геометрические фигуры, такие как треугольники, пятиугольники и девятиугольники. Для этого нужно задать нужный радиус на масштабе циркуля и затем провести острием циркуля по заранее заданным точкам, чтобы получить нужную фигуру. |
| 4. Рисование дуг и дуговых сегментов | Циркуль позволяет рисовать дуги и дуговые сегменты окружностей. Для этого нужно задать нужный радиус на масштабе циркуля и затем, удерживая один конец циркуля в центре окружности, проводить другой конец по нужной дуге. |
Циркуль - это простой, но очень полезный инструмент для работы с геометрией и создания различных геометрических фигур. Он позволяет точно измерять расстояния, создавать окружности и другие геометрические фигуры, что делает его незаменимым помощником во многих областях, связанных с конструированием и дизайном.
Понятие девятиугольника
Девятиугольники могут быть правильными, когда все их стороны и углы равны, а также неправильными, когда стороны и углы могут быть различными. Для построения правильного девятиугольника с помощью циркуля необходимо провести 9 равных дуг, используя центр и один и тот же радиус.
Обратите внимание, что точное построение правильного девятиугольника с помощью циркуля возможно только на бумаге, поскольку на плоскости реального мира нет точки, которая может быть одновременно началом и концом дуги.
Девятиугольники встречаются в различных областях математики и геометрии. Они могут быть использованы для построения других фигур, а также для решения различных задач и заданий.
Шаги по созданию девятиугольника

1. Шаг первый: Поместите ноль на центральной оси вашего листа бумаги. Это будет точка, вокруг которой вы будете рисовать девятиугольник.
2. Шаг второй: Выберите определенное расстояние на циркуле, которое будет равно радиусу девятиугольника. Установите циркуль на ноль и проведите окружность с этим радиусом вокруг точки нуля. Эта окружность станет внешней стороной девятиугольника.
3. Шаг третий: Установите циркуль на одну из точек на окружности, проведенной на предыдущем шаге. Переведите мини-компас в режим передвижения и вращайте его, чтобы найти вторую точку на окружности. Это точка станет одним из вершин девятиугольника.
4. Шаг четвертый: Повторите предыдущий шаг, устанавливая циркуль на уже найденные точки и находя следующую точку на окружности. Продолжайте этот процесс до тех пор, пока не будет найдено девять точек. Каждая из этих точек станет вершиной девятиугольника.
5. Шаг пятый: Соедините найденные вершины девятиугольника линиями. Убедитесь, что каждая вершина соединена с соседними вершинами. После этого вы получите готовый девятиугольник.
Создание девятиугольника с помощью циркуля не только развивает навыки рисования, но и тренирует концентрацию и воображение. Попробуйте этот метод и насладитесь процессом создания симметричной фигуры.
Использование циркуля для построения

- Начните с рисования центральной окружности, задав ее центр и радиус.
- С помощью циркуля установите его на одной точке окружности и проведите дугу.
- Переставьте циркуль на другую точку окружности и снова проведите дугу.
- Продолжайте перемещать циркуль по точкам окружности, проводя дуги, пока не получите девять равных дуг, соединяющих точки на окружности.
- Соедините полученные дуги внутри окружности сегментами прямых линий.
В итоге вы получите девятиугольник, вписанный в данную окружность. Использование циркуля упрощает процесс построения геометрических фигур и позволяет получить точные и симметричные результаты.
Подведение итогов

Таким образом, мы рассмотрели процедуру создания девятиугольника с помощью циркуля. Эта задача требует тщательного применения циркуля и правильной последовательности действий.
Основные этапы включают:
- Нахождение центра будущего девятиугольника.
- Построение радиуса, равного расстоянию от центра до любой вершины девятиугольника.
- Построение окружности с центром в найденной точке и радиусом, найденным на предыдущем шаге.
- Используя циркуль, построение дуг окружности так, чтобы девятиугольник описывался этими дугами.
В результате получится идеальный девятиугольник, которому будет сложно противостоять в своей геометрической красоте.
Теперь, имея эту информацию, вы можете создать свой собственный девятиугольник и впечатлить своих друзей своими навыками в геометрии!