Конструирование нод – одна из самых захватывающих и увлекательных задач в геометрии и комбинаторике. Ноды – это уникальные структуры, состоящие из точек, линий и других элементов геометрического пространства. Они представляют собой не только интересные объекты для изучения, но и мощный инструмент для решения сложных задач.
Умелое конструирование нод требует от исследователя глубокого знания геометрии и комбинаторики, а также творческого подхода к решению задач. Ноды могут иметь различные формы и свойства, и умение правильно выбирать и комбинировать элементы для их создания – это искусство, которое нужно постоянно совершенствовать.
В данной статье мы рассмотрим несколько секретов умелого конструирования нод, которые помогут вам стать более опытным исследователем в геометрии и комбинаторике. Мы рассмотрим методы создания нод с использованием различных симметрий, алгоритмов построения и комбинирования элементов. Кроме того, мы рассмотрим примеры практического применения нод в решении различных задач.
Точки и прямые в двумерной геометрии
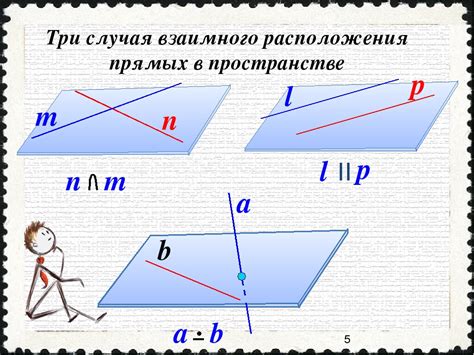
Прямая - это объект, который имеет бесконечную длину и ширину, но не имеет толщины. Прямая обозначается маленькой латинской буквой или полужирной латинской буквой, например, a, b, c или А, В, С и т.д.
Существует несколько способов задания прямых в двумерной геометрии. Одним из способов задания прямых является уравнение прямой в декартовой системе координат. Уравнение прямой имеет вид y = kx + b, где k - это коэффициент наклона прямой, а b - свободный член. Зная коэффициенты уравнения прямой, можно определить ее положение и поведение относительно осей координат.
Также прямые могут быть заданы геометрически, например, через задание двух точек, через задание точки и направления, или через задание точек и угла наклона. Зная координаты двух точек на прямой или точку и направление, можно однозначно определить уравнение прямой.
| Способ задания прямой | Уравнение прямой |
|---|---|
| Через две точки | y - y₁ = (y₂ - y₁) / (x₂ - x₁) * (x - x₁) |
| Через точку и направление | y - y₁ = k(x - x₁) |
| Через точки и угол наклона | y = kx + b |
Знание основных свойств и способов задания точек и прямых в двумерной геометрии является основой для решения различных геометрических задач, а также для построения сложных фигур и структур.
Методика построения треугольников
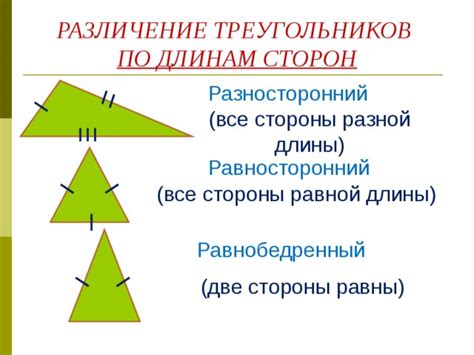
- Построение треугольника по длинам сторон: Если известны длины всех трех сторон треугольника, то его можно построить с помощью компаса и линейки. Необходимо взять произвольную точку A, затем провести поочередно отрезки AB, BC и AC, где AB, BC и AC – известные длины сторон. Точка C будет получена пересечением прямых AB и BC, а точка B – пересечением прямых AB и AC.
- Построение треугольника по длине одной стороны и двум углам: Если известна длина одной стороны треугольника и меры двух углов, то его также можно построить с помощью компаса и линейки. Взяв произвольную точку A и отрезок AB, равный известной длине стороны, следует отложить измеренные углы от точки B, получив точки C и D. Точки B, C и D являются вершинами искомого треугольника.
- Построение треугольника по длине двух сторон и углу между ними: Если известны длины двух сторон треугольника и мера угла, образованного этими сторонами, то треугольник также можно построить. Необходимо взять произвольную точку A и провести отрезок AB, равный известной длине одной из сторон. Затем от угла A отложить измеренный угол, получив точку C. Проведя отрезок BC, равный известной длине второй стороны, получим треугольник ABC.
Это основные методики построения треугольников, которые важно знать при решении геометрических задач.
Построение треугольника по трем сторонам
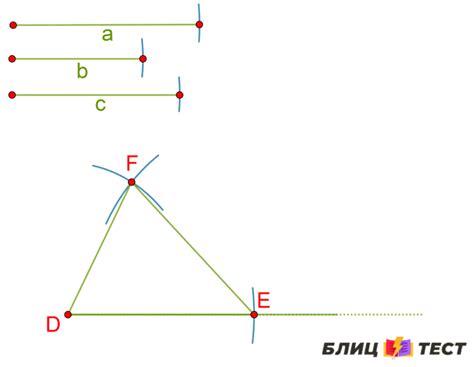
Для начала, можно использовать свойство неравенства треугольника: сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Если это свойство выполняется для заданных сторон, то треугольник с такими сторонами существует.
Если стороны треугольника заданы, можно найти его площадь, используя формулу Герона. Площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разности полупериметра и длины каждой стороны. Зная площадь треугольника, можно определить его высоту.
Если треугольник нужно построить на плоскости, то можно использовать координаты его вершин. Зная координаты трех вершин треугольника, можно найти его стороны и углы. Затем, используя полученные значения, можно построить треугольник на плоскости.
Построение треугольника по трем сторонам - это важная задача в геометрии, которая находит применение в различных областях знаний. Она помогает определить форму и размеры объектов, а также решать разнообразные задачи конструирования и расчета. Зная основные методы и приемы, можно успешно строить треугольники и использовать их свойства для решения разнообразных задач.
Построение треугольника по двум сторонам и углу
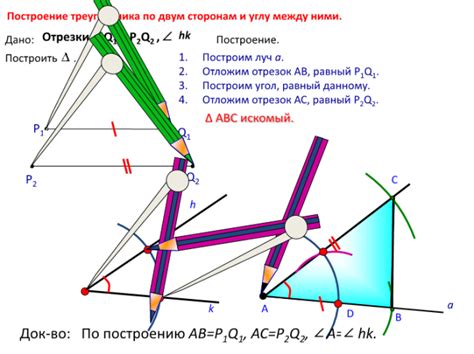
Для построения треугольника по двум сторонам и углу необходимо следовать определенным шагам. Данный метод позволяет построить треугольник с высокой точностью и минимальными погрешностями.
Шаг 1: Найдите точку A и отметьте ее на листе бумаги. Она будет являться одним из вершин треугольника.
Шаг 2: Из точки A отложите первую сторону треугольника AB, такую, что ее длина соответствует заданной стороне треугольника.
Шаг 3: Из точки B отложите вторую сторону треугольника BC, такую, что ее длина соответствует заданной стороне треугольника. Угол ABC должен быть таким, что его величина совпадает с заданным углом треугольника.
Шаг 4: Вершина треугольника C будет являться пересечением прямых, заданных сторонами AB и BC.
| Шаг | Описание действия | Демонстрация |
|---|---|---|
| Шаг 1 | Найдите точку A и отметьте ее на листе бумаги. |  |
| Шаг 2 | Отложите первую сторону AB, длина которой соответствует заданной стороне треугольника. |  |
| Шаг 3 | Отложите вторую сторону BC и угол ABC. |  |
| Шаг 4 | Вершина треугольника C - пересечение прямых AB и BC. |  |
Таким образом, в результате выполнения всех шагов вы построите треугольник по двум сторонам и углу.
Квадраты, прямоугольники и кубы
Квадрат - это специальный вид прямоугольника, у которого все стороны равны. Он обладает рядом интересных свойств, которые делают его полезным для конструирования. Например, квадраты могут быть использованы для построения геометрических фигур, а также для исследования и доказательства различных теорем.
Прямоугольник - это частный случай параллелограмма, у которого все углы прямые. Прямоугольники также имеют ряд уникальных свойств, которые делают их полезными для конструирования. Например, прямоугольники могут быть использованы для построения различных полигонов, а также для моделирования и изучения различных пространственных объектов.
Куб - это трехмерная фигура, у которой все грани являются квадратами. Кубы также имеют ряд интересных свойств, которые делают их полезными и увлекательными для изучения. Например, кубы могут быть использованы для конструирования и исследования различных трехмерных моделей, а также для решения задач в комбинаторике и теории графов.
Изучение и использование квадратов, прямоугольников и кубов является важным элементом в геометрии и комбинаторике. Они предоставляют широкий спектр возможностей для конструирования, моделирования и решения задач в этих областях математики.
Конструирование квадрата с данной стороной
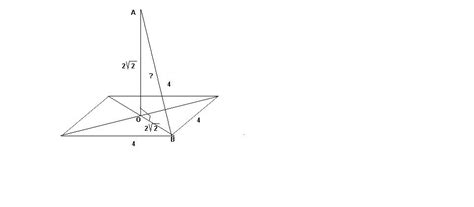
Для начала, необходимо взять рулетку или линейку и отметить на листе бумаги отрезок с длиной, соответствующей значению стороны квадрата. Затем, используя циркуль или шаблон, проведите две перпендикулярные прямые через эти точки, чтобы образовать прямоугольник.
Далее, используя циркуль, возьмите одну из сторон получившегося прямоугольника и откройте его на такое же расстояние, как и сторона прямоугольника. Нарисуйте дугу, проходящую через эту точку и пересекающую другую сторону прямоугольника. Проведите прямую через эту точку и центр окружности, образованной дугой. Отметьте точку пересечения этой прямой со второй стороной прямоугольника.
Теперь, используя полученные точки, проведите прямые линии, соединяющие их друг с другом. Эти прямые образуют четыре стороны и четыре угла квадрата, соответствующие данной стороне.
Наконец, чтобы завершить конструкцию, удалите все вспомогательные линии и получите искомый квадрат с заданной стороной.
Конструирование квадрата с данной стороной является важным навыком, который может быть использован в различных областях, таких как архитектура, дизайн или строительство. При использовании правильных методов и инструментов, можно легко и точно создать квадрат с заданными размерами.
Построение прямоугольника с данными сторонами
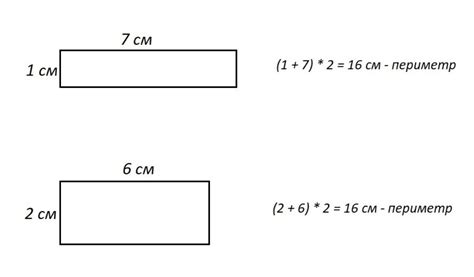
Для построения прямоугольника с данными сторонами необходимо выполнить следующие шаги.
1. Возьмите лист бумаги и ручку. На листе бумаги чертите две параллельные прямые линии, которые будут соответствовать сторонам прямоугольника.
2. Измерьте заданные стороны прямоугольника с помощью линейки и отметьте нужные отрезки на прямых линиях.
3. Соедините отмеченные точки на прямых линиях, чтобы получить четырехугольник.
4. Проверьте, что углы прямоугольника совпадают и все стороны равны заданным значениям. Если нет, убедитесь, что вы правильно измерили и отметили стороны.
5. Если прямоугольник был успешно построен, можно его закрасить, чтобы было проще видеть форму.
Теперь вы знаете, как построить прямоугольник с данными сторонами. Такой навык может быть полезен при решении задач геометрии, разработке архитектурных проектов и других областях, где требуется точное представление прямоугольников.
Построение куба с данным ребром
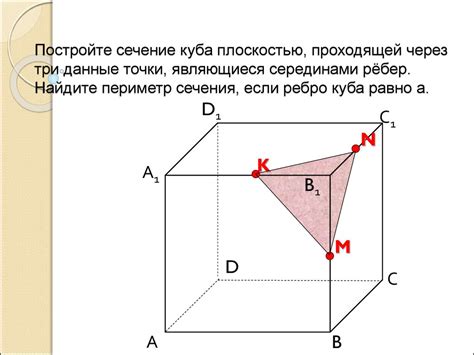
Для начала, возьмем ребро заданной длины и проведем прямую линию. Затем, на этой линии выберем точку и построим прямые, параллельные и перпендикулярные этой линии.
Затем, используя эти прямые, построим квадрат на верхней грани и получим верхнюю грань куба. После этого, построим остальные грани куба, основываясь на верхней грани.
Для построения боковых граней куба, необходимо провести прямые, параллельные сторонам верхнего квадрата. Затем, используя эти прямые, построим боковые грани куба.
Таким образом, используя данные конструкции и алгоритмы, можно построить куб с заданным ребром. Эта задача является одной из фундаментальных задач в геометрии и комбинаторике, и ее решение имеет важное значение в различных областях науки и инженерии.
Комбинаторика и графы

В комбинаторике задействованы различные методы и техники, которые позволяют находить комбинаторные структуры и решать различные задачи, связанные с подсчетом и размещением объектов. Комбинаторные числа, комбинаторные формулы и комбинаторные конструкции играют важную роль в графах и других областях математики.
Графы представляют собой абстрактные структуры, состоящие из вершин и ребер. Вершины представляют объекты, а ребра представляют связи между объектами. Графы могут быть ориентированными или неориентированными, взвешенными или невзвешенными, связными или несвязными. Графы используются для моделирования различных ситуаций, таких как сети связи, социальные сети, транспортные сети, графики и алгоритмы.
Взаимодействие комбинаторики и графов позволяет исследовать различные комбинаторные свойства графов и применять комбинаторные методы для решения графовых задач. Например, теория графов может использоваться для изучения комбинаторных оптимизаций, как например, нахождение минимального остовного дерева или кратчайшего пути в графе.
Таким образом, понимание комбинаторики и графов важно для развития и применения различных конструкций и решений в геометрии и комбинаторике. Они предоставляют мощные инструменты для анализа и моделирования сложных систем и позволяют находить эффективные решения в различных областях.