Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. Часто на плоскости при решении геометрических задач необходимо найти различные параметры этого треугольника, например, биссектрису. Биссектриса – это линия, которая делит угол на две равные части. Но как найти биссектрису равнобедренного треугольника по заданным сторонам? Давайте разберемся.
Для начала, нужно вычислить углы равнобедренного треугольника. Пусть a, b и c – стороны треугольника. По определению равнобедренного треугольника, a = b. Чтобы найти углы, необходимо использовать теорему косинусов.
Зная длины сторон треугольника, можно найти значения косинусов углов. Пусть A, B и C – углы треугольника. Тогда можно воспользоваться формулой: cos(A) = (b^2 + c^2 - a^2) / (2bc), cos(B) = (a^2 + c^2 - b^2) / (2ac), cos(C) = (a^2 + b^2 - c^2) / (2ab). Решив эти уравнения относительно углов A, B и C, мы получим значения углов равнобедренного треугольника.
Что такое биссектриса равнобедренного треугольника
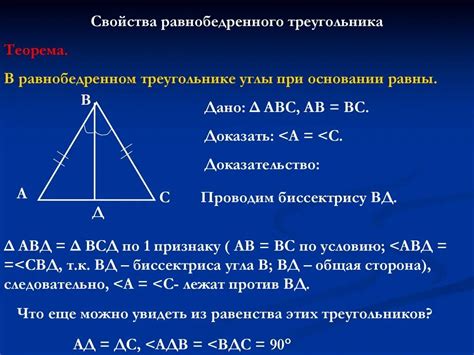
Булыжник, так же известный как уголник, используется для построения биссектрисы. Он состоит из трех отрезков с маркировками. Уголник легко переносится на основание треугольника, где его центральный отрезок будет совпадать с биссектрисой. После этого достаточно провести прямую через вершину треугольника, которая будет являться искомой биссектрисой.
Зная длины сторон равнобедренного треугольника, можно легко вычислить длину биссектрисы с помощью формулы:
- Длина биссектрисы = sqrt(st * sb * (st + sb + 2 * sa)) / (st + sb),
где st - длина основания, а sa и sb - длины равных боковых сторон треугольника.
Как свойство равнобедренного треугольника, биссектриса также является медианой и высотой треугольника. Это означает, что она делит основание и гипотенузу на две равные части и перпендикулярна им.
Биссектриса равнобедренного треугольника играет важную роль в геометрии. Она может быть использована для нахождения точки пересечения биссектрис других углов треугольника, а также для нахождения площади треугольника или его высот.
Как найти биссектрису равнобедренного треугольника

Чтобы найти биссектрису равнобедренного треугольника, нужно выполнить следующие шаги:
Шаг 1: Найдите длины сторон равнобедренного треугольника. Обозначим эти длины как a, a и b, где a - длина равных сторон, а b - длина основания.
Шаг 2: Рассчитайте полупериметр треугольника по формуле: p = (a + a + b) / 2.
Шаг 3: Найдите площадь треугольника по формуле Герона: s = sqrt(p * (p - a) * (p - a) * (p - b)).
Шаг 4: Найдите высоту треугольника, проведенную к основанию, по формуле: h = (2 * s) / b.
Шаг 5: Постройте биссектрису, соединив вершину треугольника с точкой деления основания высотой на две равные части.
Теперь у вас есть информация о том, как найти биссектрису равнобедренного треугольника по сторонам. Этот метод может быть полезен при решении геометрических задач или построении треугольников с заданными условиями.
Формула для расчета биссектрисы равнобедренного треугольника
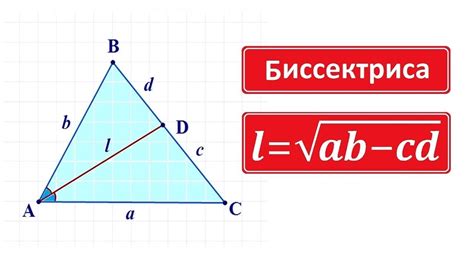
Биссектриса равнобедренного треугольника — это отрезок, который делит угол треугольника на два равных угла. Для расчета биссектрисы равнобедренного треугольника существует специальная формула, основанная на известных сторонах треугольника.
Пусть a и b — это две равные стороны равнобедренного треугольника, а c — третья сторона. Формула для расчета биссектрисы (i) выглядит следующим образом:
i = sqrt(ab(а + b + c)(-ab + a + b + c)) / (a + b).
В этой формуле "sqrt" означает квадратный корень. Таким образом, чтобы найти биссектрису равнобедренного треугольника, нужно знать значения длин двух равных сторон (a и b) и длину третьей стороны (c).
Формула позволяет рассчитать точную длину биссектрисы. После расчета можно использовать полученное значение для дальнейших вычислений или построения графиков в зависимости от конкретной задачи.
Пример нахождения биссектрисы равнобедренного треугольника
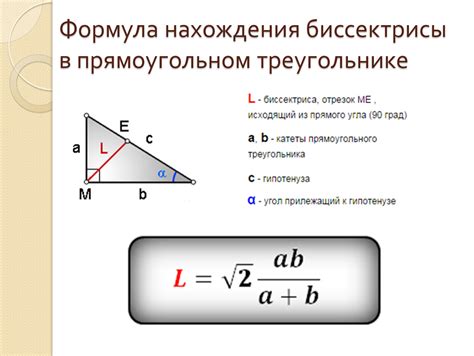
Давайте рассмотрим пример нахождения биссектрисы равнобедренного треугольника с основанием a и боковой стороной b.
| Дано: | Искомое: |
|---|---|
| Основание a | Биссектриса |
| Боковая сторона b |
Для нахождения биссектрисы равнобедренного треугольника применим следующую формулу:
Биссектриса = √(a^2 + b^2) / 2
В данной формуле используется теорема Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы:
a^2 + b^2 = c^2
где a - основание треугольника, b - боковая сторона треугольника, c - гипотенуза (биссектриса).
Теперь, зная основание a и боковую сторону b, мы можем вычислить биссектрису равнобедренного треугольника с помощью формулы:
Биссектриса = √(a^2 + b^2) / 2
Например, если основание треугольника a = 5 и боковая сторона b = 6, то:
Биссектриса = √(5^2 + 6^2) / 2 = √(25 + 36) / 2 = √61 / 2 ≈ 3.92
Таким образом, в примере, биссектриса равнобедренного треугольника с основанием 5 и боковой стороной 6 равна примерно 3.92.