Шестиугольник – это многоугольник, состоящий из шести сторон и шести углов. В геометрии шестиугольники часто встречаются и являются объектом большого интереса. Одним из способов разгадать их тайну является нахождение их градусной меры.
Для начала нужно знать, что сумма всех внутренних углов любого многоугольника равна 180 градусам. Следовательно, чтобы найти градусную меру шестиугольника, необходимо разделить эту сумму на количество углов, то есть на 6. Ответом будет 30 градусов.
Однако, существует и другой способ нахождения градусной меры шестиугольника, основанный на правильности его структуры. Если шестиугольник является правильным, то все его стороны и углы равны между собой. В таком случае, градусная мера каждого угла будет равна 120 градусам, так как сумма всех углов должна равняться 720 градусам (180 градусов у треугольника, умноженные на количество треугольников – 6).
Что такое шестиугольник: определение и свойства

Шестиугольник обладает рядом интересных свойств:
- Сумма всех углов шестиугольника равна 720 градусов.
- Внутренние углы шестиугольника могут быть равными или различными.
- Шестиугольник является выпуклым, то есть все его углы меньше 180 градусов.
- Шестиугольник может быть правильным, если все его стороны и углы равны.
- Если известна длина одной стороны правильного шестиугольника, можно найти длины всех остальных сторон и прилегающих углов, используя тригонометрические функции.
Шестиугольники широко встречаются в природе, в архитектуре и в различных областях науки. Их уникальная форма дает им устойчивость и эстетическую привлекательность, что делает их популярными для использования в декоративных и искусственных объектах.
Какие углы в шестиугольнике: формула для нахождения суммы углов

Сумма углов в любом многоугольнике равна (n-2) × 180, где n – количество сторон многоугольника. В случае шестиугольника, где n = 6, формула примет следующий вид:
(6-2) × 180 = 4 × 180 = 720
Таким образом, сумма углов в шестиугольнике равна 720 градусов.
Как можно заметить, сумма углов в шестиугольнике составляет в два раза больше суммы углов в треугольнике, так как шестиугольник состоит из трех треугольников.
Зная сумму углов шестиугольника, можно также вычислить меру каждого угла, разделив сумму на количество углов. В случае шестиугольника это будет:
720 градусов ÷ 6 углов = 120 градусов
Таким образом, каждый угол в шестиугольнике имеет меру 120 градусов.
Способы нахождения одного угла в шестиугольнике
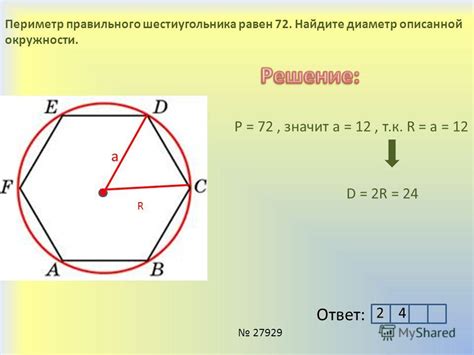
- Сумма углов внутри шестиугольника: Один из способов нахождения градусной меры одного угла шестиугольника основывается на сумме углов внутри фигуры. Шестиугольник имеет 6 углов, и сумма градусных мер всех углов внутри него всегда равна 720 градусов. Следовательно, чтобы найти градусную меру одного угла, нужно разделить 720 на 6.
- Разделение на треугольники: Еще один метод нахождения градусной меры угла в шестиугольнике заключается в разделении фигуры на треугольники. Шестиугольник можно разделить на 4 треугольника, используя диагонали фигуры. Затем можно вычислить градусную меру каждого треугольника, а затем сложить их значения, чтобы получить градусную меру одного угла.
- Симметричность углов: Шестиугольник является правильной фигурой, у которой все стороны и углы равны. Это означает, что каждый угол шестиугольника имеет одинаковую градусную меру. Для нахождения градусной меры одного угла можно разделить 360 градусов (сумма градусных мер всех углов внутри фигуры) на 6.
Эти методы помогут вам находить градусную меру одного угла в шестиугольнике, что может быть полезным в геометрических расчетах и при решении задач различной сложности.
Как найти градусную меру всех углов в шестиугольнике: общая формула
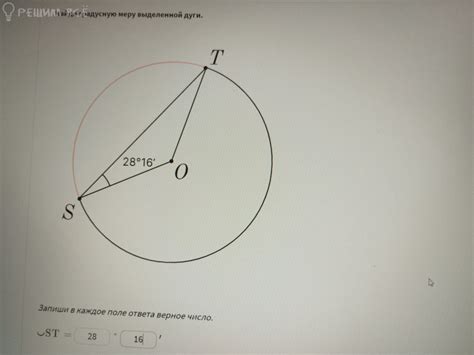
Градусная мера каждого угла в шестиугольнике может быть найдена с помощью общей формулы, основанной на свойствах геометрических фигур.
Шестиугольник состоит из шести углов, обозначаемых как A, B, C, D, E и F. Для того чтобы найти градусную меру каждого угла, следует использовать следующую формулу:
| Градусная мера угла A | = (6 - 2) * 180° / 6 |
| Градусная мера угла B | = (6 - 2) * 180° / 6 |
| Градусная мера угла C | = (6 - 2) * 180° / 6 |
| Градусная мера угла D | = (6 - 2) * 180° / 6 |
| Градусная мера угла E | = (6 - 2) * 180° / 6 |
| Градусная мера угла F | = (6 - 2) * 180° / 6 |
В этой формуле, шестерка (6) представляет количество углов в шестиугольнике, и каждый угол разделен на 180°.
Применение этой формулы позволяет найти градусную меру каждого угла в шестиугольнике. Данная формула может использоваться для любого шестиугольника, независимо от его размеров и формы.
Как использовать теорему о сумме углов треугольника для нахождения углов шестиугольника
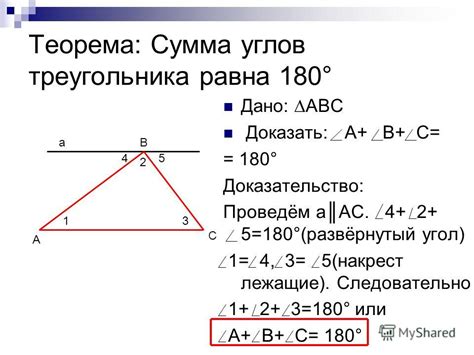
Чтобы найти градусную меру углов в шестиугольнике, можно воспользоваться теоремой о сумме углов треугольника. Теорема гласит, что сумма всех углов в треугольнике равна 180 градусам.
Шестиугольник можно разделить на четыре треугольника, проведя диагонали от одного вершины до другой. Таким образом, шестиугольник будет состоять из шести треугольников.
Затем мы можем использовать теорему о сумме углов треугольника для каждого из этих треугольников. Для каждого треугольника найдем сумму двух его углов, затем отнимем полученную сумму от 180 градусов, чтобы найти меру третьего угла.
После того, как мы найдем градусные меры трех углов каждого треугольника, суммируем их, чтобы получить меру одного угла шестиугольника. Затем умножим это значение на 6, так как в шестиугольнике шесть углов, чтобы найти общую градусную меру всех углов.
Таким образом, используя теорему о сумме углов треугольника, можно найти градусную меру всех углов шестиугольника и решить задачу.
Варианты применения тригонометрических функций для нахождения углов шестиугольника
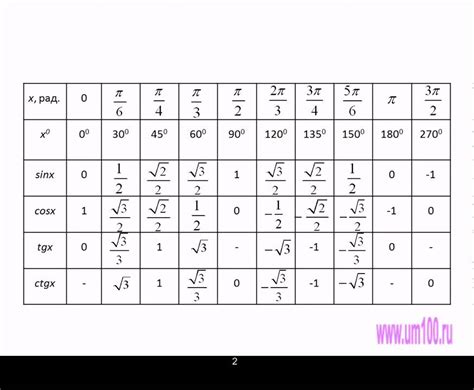
Тригонометрические функции могут быть полезны для вычисления углов шестиугольника, особенно если известны значения сторон фигуры.
1. Использование синуса: если известны значения сторон шестиугольника, то можно использовать обратный синус для вычисления углов. Для этого необходимо разделить значение противоположной стороны на значение гипотенузы и применить обратную функцию синуса.
2. Использование косинуса: для вычисления углов шестиугольника можно также использовать косинус. Если известны значения двух сторон и угла между ними, то можно применить теорему косинусов для определения третьей стороны. Затем, используя обратную функцию косинуса, можно найти значение угла.
3. Использование тангенса: если известны значения сторон, можно также использовать тангенс для вычисления углов. Для нахождения угла необходимо разделить значение противоположной стороны на значение прилежащей стороны и применить обратную функцию тангенса.
4. Использование инверсных тригонометрических функций: для нахождения углов шестиугольника можно использовать также инверсные тригонометрические функции, такие как арксинус, арккосинус и арктангенс. Эти функции применяются для нахождения углов, когда известны значения сторон или отношений между сторонами.
В итоге, применение тригонометрических функций позволяет вычислить углы шестиугольника, если известны значения сторон или отношений между сторонами. Зная углы, можно проводить дополнительные расчеты и анализировать свойства данной фигуры.
Примеры решения задач: конкретные значения углов в шестиугольнике
Чтобы найти градусную меру углов в шестиугольнике, можно воспользоваться следующей формулой:
Градусная мера каждого угла в равностороннем шестиугольнике равна 180 градусов, деленных на число вершин. В случае шестиугольника это будет:
180 / 6 = 30 градусов
Таким образом, каждый угол шестиугольника равен 30 градусам.
Пример:
Пусть дан шестиугольник ABCDEF. Нам нужно найти градусную меру каждого из его углов.
Используя формулу, мы получаем:
Градусная мера каждого угла = 180 / (число вершин)
Градусная мера каждого угла = 180 / 6
Градусная мера каждого угла = 30 градусов
Таким образом, каждый угол шестиугольника ABCDEF равен 30 градусам.