Площадь прямоугольника – одна из базовых геометрических характеристик этой фигуры, которая важна не только для математиков, но и для всех, кто желает понять и применить ее в реальной жизни. Это понятие регулярно используется в архитектуре, строительстве, дизайне интерьера, инженерии, и даже в разработке программного обеспечения.
Как найти площадь прямоугольника? Для этого достаточно знать длину и ширину прямоугольника и применить простую математическую формулу: S = a * b, где a – длина, b – ширина. Очень важно правильно определить единицы измерения – метры, сантиметры, дюймы или другие, и использовать их в расчетах. Если площадь задана в квадратных единицах (например, квадратных метрах), то ответом будет число, а если в других единицах, то ответом будет число с указанием единицы измерения.
Для ускорения расчетов площади прямоугольника в пространстве существует множество методов и техник. Например, в программировании используются алгоритмы, которые позволяют автоматизировать этот процесс. Они позволяют обрабатывать и анализировать большие объемы данных и выполнять сложные математические операции за считанные секунды. Также существуют специальные онлайн-калькуляторы и приложения, которые упрощают расчеты площади прямоугольника и позволяют быстро получать точные результаты.
Простой способ найти площадь прямоугольника
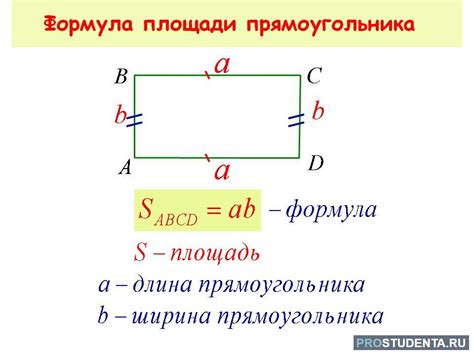
В математике площадь прямоугольника определяется как произведение его длины на ширину. Для быстрого и простого расчета площади прямоугольника необходимо знать только эти два параметра.
Допустим, у нас есть прямоугольник с длиной а и шириной b. Чтобы найти его площадь, нужно умножить длину на ширину:
Площадь = а * b
Например, если длина прямоугольника равна 5 см, а ширина - 3 см, его площадь будет:
Площадь = 5 * 3 = 15 см²
Таким образом, общий способ нахождения площади прямоугольника заключается в умножении длины на ширину.
Использование этого простого математического правила позволяет быстро и эффективно рассчитывать площадь прямоугольников в любых задачах или приложениях, где необходимо определить площадь поверхности.
Прямоугольник: базовые определения и свойства
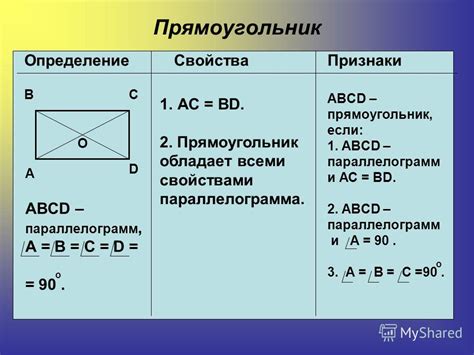
Свойства прямоугольников:
1. Диагонали прямоугольника равны между собой и делят фигуру на два равных треугольника.
2. Периметр прямоугольника равен сумме всех его сторон: P = 2(a + b), где P – периметр, а и b – длины сторон.
3. Площадь прямоугольника равна произведению его длины и ширины: S = a * b, где S – площадь, a – длина, b – ширина.
| Диагональ прямоугольника | Периметр прямоугольника | Площадь прямоугольника |
 |  |  |
Прямоугольники широко применяются в геометрии, инженерии, архитектуре, дизайне и других областях. Знание и использование их свойств позволяет выполнять различные расчеты и построения в пространстве.
Формула расчета площади прямоугольника
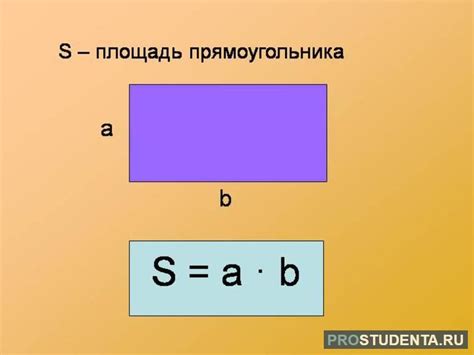
Площадь прямоугольника можно найти, умножив его длину на ширину. Данная формула применима к любым прямоугольникам, независимо от их размеров.
Формула расчета площади прямоугольника имеет вид:
S = a * b,
где S - площадь прямоугольника, a - длина, b - ширина.
Например, пусть длина прямоугольника a = 5 см, а ширина b = 3 см. Тогда площадь прямоугольника S будет равна:
S = 5 * 3 = 15 см².
Таким образом, площадь прямоугольника равна 15 квадратным сантиметрам.
Ускорение расчетов в пространстве
В одной из таких задач, расчет площади прямоугольника, существуют разные подходы для ускорения процесса. Одним из них является использование алгоритма Монте-Карло. Суть алгоритма заключается в том, что мы генерируем случайные точки внутри прямоугольника и считаем, какая доля точек попала внутрь прямоугольника. Затем, умножая эту долю на площадь прямоугольника, получаем приближенное значение его площади.
Другим подходом для ускорения расчетов может быть использование графических процессоров (GPU). GPU имеют большую параллельную вычислительную мощность и могут эффективно обрабатывать задачи, связанные с графикой и расчетами в пространстве. Задачи, такие как нахождение площади прямоугольника, могут быть распараллелены и обработаны с использованием GPU, что значительно увеличит скорость расчетов.
Кроме того, эффективное использование алгоритмов, таких как быстрое преобразование Фурье (FFT), может помочь в ускорении расчетов в пространстве. FFT позволяет в кратчайшие сроки решать задачи, связанные с обработкой сигналов и преобразованием данных. Применение FFT к задачам, таким как нахождение площади прямоугольника, может значительно сократить время выполнения расчетов.
Таким образом, существует несколько способов ускорить расчеты в пространстве, включая использование алгоритма Монте-Карло, применение графических процессоров и эффективное использование алгоритмов, таких как FFT. Выбор подходящего метода зависит от специфики задачи и требований к скорости расчетов.