Секреты нахождения производной при возведении x в степень, которые улучшат вашу математику

Производные являются ключевым понятием в математике, особенно при исследовании и определении характеристик функций. Наиболее простыми функциями, у которых необходимо находить производные, являются степенные функции. Одним из базовых правил дифференцирования является нахождение производной функции, возведенной в степень.

Дифференцирование функции, в которой основой является x, позволяет найти производную при возведении в степень другой функции. Если дана функция f(x), равная возведению x в степень n, то ее производная определяется следующим образом: производная f(x) равняется частному произведения n и x, возведенных в степень n-1.

Таким образом, если имеется функция f(x) = x^n, то ее производная f'(x) = n * x^(n-1). Данный метод дифференцирования также может применяться, когда степень не является целым числом, а представляет собой десятичную или рациональную дробь.

Определение производной

Формально, производная функции определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Это может быть записано математически в виде:

В данной формуле x - это аргумент функции, n - степень, в которую возводится аргумент.

Определение производной для функции возведения x в степень позволяет найти коэффициент при x, который обозначает скорость изменения значения функции при изменении аргумента x. Вычисление производной позволяет более точно определить изменения величины и применить их в различных областях, таких как физика, экономика и технические науки.

Формула для производной при возведении в степень

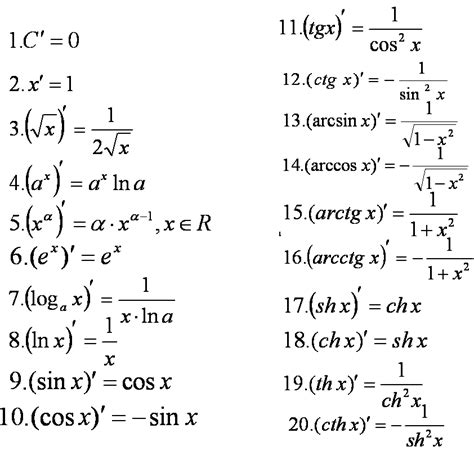
При работе с функциями, содержащими возведение в степень, необходимо знать формулу для производной таких функций. Производная функции, в которой исходная функция представлена символом x, возведенным в степень n, равна произведению n и производной этой функции . То есть, если у нас есть функция f(x) = x^n, то ее производная будет равна d(x^n)/dx = n*x^(n-1).

Таким образом, для любой функции, в которой имеется возведение в степень, можно легко найти производную, применяя данную формулу. Например, для функции f(x) = x^3, производная будет равна d(x^3)/dx = 3*x^(3-1) = 3*x^2.

Используя данную формулу, можно находить производные при возведении в любую степень и получать точные значения производных для данных функций.

Основной раздел

f'(x) = n * x^(n-1)

Для подсчета производной такой функции необходимо умножить старшую степень переменной на коэффициент, образованный из старшей степени исходной функции, уменьшенной на единицу.

Например, для функции f(x) = x^3 производная будет равна:

f'(x) = 3 * x^(3-1) = 3 * x^2

Полученная формула позволяет находить производные функций с переменной, возведенной в произвольную степень. Важно помнить, что производная функции в такой форме всегда будет являться многочленом с переменной, уменьшенной на 1 в степени.

Примеры вычислений производной

Для лучшего понимания процесса вычисления производной при возведении x в степень можно рассмотреть несколько примеров:

Пример 1:

Рассмотрим функцию f(x) = x². Чтобы найти производную этой функции, нужно использовать правило дифференцирования степенной функции, которое гласит: если функция имеет вид f(x) = xⁿ, то ее производная равна f'(x) = n*x^n-1.

В нашем случае, функция f(x) = x², поэтому производная будет равна f'(x) = 2*x^2-1 = 2*x.

Пример 2:

Рассмотрим функцию g(x) = x³. Применяя тот же принцип, получим производную g'(x) = 3*x^3-1 = 3*x².

Пример 3:

Рассмотрим функцию h(x) = x⁴. Производная h'(x) = 4*x^4-1 = 4*x³.

Таким образом, примеры вычислений производной при возведении x в степень показывают, что производная степенной функции имеет вид произведения показателя степени и основания возведения в степень.

Особые случаи и исключения

При нахождении производной функции, где x возведено в степень, существуют несколько особых случаев и исключений, которые стоит учитывать.

1. Производная константы: При нахождении производной выражения вида c, где c - любая константа, производная будет равна нулю. То есть, производная от c равна 0.

2. Производная x в степени нуль: Производная выражения x^0, где x - переменная, будет равна нулю. То есть, производная от x^0 равна 0.

3. Производная x в степени единицы: Производная выражения x^1, где x - переменная, будет равна 1. То есть, производная от x^1 равна 1.

4. Производная неконстантной степени: При нахождении производной выражения x^n, где x - переменная, а n - неконстантное значение, следует использовать правило степенной функции. Производная будет равна n*x^(n-1). То есть, производная от x^n равна n*x^(n-1).

Это основные особые случаи и исключения, которые могут возникнуть при нахождении производной выражения с возведением x в степень. Они помогут вам более точно и эффективно находить производные в подобных случаях.