Оптимизация функций является одной из важных задач в области науки и инженерии. Она позволяет находить оптимальные значения параметров для моделей и систем, что в свою очередь способствует улучшению их работы и повышению качества и эффективности. Одним из инструментов оптимизации, широко используемым в MATLAB, является функция fminsearch.
Функция fminsearch осуществляет поиск минимума заданной функции с помощью алгоритма оптимизации Нелдера-Мида. Она является основным инструментом в MATLAB для решения задач оптимизации без ограничений. Fminsearch использует итерационный метод пошагового уточнения для нахождения минимума функции.
Одним из ключевых секретов работы с функцией fminsearch является выбор правильной задачи оптимизации. Необходимо ясно определить, какая именно функция требует оптимизации, а также какие параметры должны быть подвергнуты оптимизации. Также стоит учесть, что fminsearch позволяет работать только с невекторными функциями. Если ваша задача оптимизации включает в себя векторные функции, вам придется провести необходимые преобразования.
Для эффективного использования fminsearch рекомендуется провести предварительный анализ функции и ее области определения. Необходимо изучить особенности функции, такие как локальные и глобальные минимумы, достаточные условия оптимизации и ограничения на параметры. Знание точек, в которых функция достигает минимума или имеет особые значения, поможет вам выбрать правильную стратегию оптимизации и подобрать подходящие параметры для fminsearch.
Как использовать fminsearch для оптимизации функции
Для начала работы с функцией fminsearch необходимо определить саму целевую функцию, которую вы хотите оптимизировать. Эта функция должна принимать входные параметры и возвращать значение, которое нужно минимизировать.
Пример использования fminsearch для оптимизации функции:
% Определяем целевую функцию
fun = @(x) x^2 + sin(x);
% Задаем начальное приближение
x0 = 1;
% Запускаем оптимизацию
x = fminsearch(fun, x0);
fprintf('Минимум функции: %f
', x); При использовании fminsearch можно задать дополнительные параметры, такие как ограничения на значения переменных или дополнительные параметры для целевой функции. Эти параметры передаются в виде дополнительных аргументов в функцию fminsearch.
Использование fminsearch для оптимизации функций позволяет найти наилучшие значения переменных, при которых достигается минимум функции. Этот метод является эффективным инструментом для решения различных задач оптимизации и нахождения оптимальных значений в научных и инженерных задачах.
Определение и цель
Цель использования функции fminsearch - найти глобальный минимум функции с заданными ограничениями и начальной точкой. Это может быть полезно в различных областях, таких как экономика, физика, инженерия и другие.
Функция fminsearch принимает в качестве входных параметров функцию, которая возвращает значение функции в заданной точке, начальную точку оптимизации, а также другие необязательные параметры, такие как ограничения и параметры алгоритма оптимизации.
Задача fminsearch заключается в минимизации целевой функции, путем пошагового изменения значений входных переменных. Алгоритм Nelder-Mead, который используется внутри fminsearch, применяет различные операции, такие как отражение, расширение и сжатие, чтобы найти оптимальное значение функции.
После завершения работы fminsearch возвращает найденное оптимальное решение и значение функции в этой точке. Это позволяет проводить дальнейший анализ и использовать результаты оптимизации в дальнейших вычислениях.
Функции и алгоритмы оптимизации
Алгоритмы оптимизации могут быть различными и выбор конкретного алгоритма зависит от ряда факторов, включая характеристики задачи, доступные ресурсы и требуемую точность результата.
Существует множество различных алгоритмов оптимизации, каждый из которых имеет свои преимущества и недостатки. Некоторые алгоритмы являются итерационными, то есть требуют нескольких проходов по функции для получения оптимального решения. Другие алгоритмы могут быть более эффективными в случае, когда доступны аналитические производные или ограничения на переменные.
В контексте работы с функцией fminsearch, алгоритм оптимизации основан на поиске точки минимума функции. Данный алгоритм является итерационным и использует комбинацию методов поиска для нахождения оптимального решения. Алгоритм fminsearch широко используется в различных областях, включая оптимизацию параметров моделей, решение систем уравнений и многие другие задачи оптимизации.
Правильный выбор функции и алгоритма оптимизации может существенно повлиять на результаты оптимизации. При выборе функции и алгоритма оптимизации необходимо учитывать специфику задачи и ограничения на переменные. Некорректный выбор функции и алгоритма оптимизации может привести к неверным результатам или затратам большого количества ресурсов времени и вычислительной мощности.
Важно провести изначальный анализ задачи и выбрать наиболее подходящий алгоритм для оптимизации функции. При этом стоит помнить, что определенный алгоритм может быть эффективным для одних задач и неэффективным для других. Поэтому также важно проводить тестирование и сравнение различных алгоритмов оптимизации перед применением в конкретной задаче.
Использование правильного алгоритма оптимизации в комбинации с функцией fminsearch позволяет получить более точные и эффективные результаты оптимизации. Знание основных алгоритмов оптимизации и их особенностей поможет выбрать наиболее подходящий алгоритм и достичь оптимального решения для задачи оптимизации.
Работа с fminsearch

Для начала работы с fminsearch нужно определить оптимизируемую функцию и начальное приближение. Функция, которую необходимо минимизировать, должна быть задана в виде отдельного файла или анонимной функции.
После определения функции и начального приближения можно вызвать fminsearch с указанием этих параметров. Функция возвращает найденное минимальное значение функции и вектор, соответствующий найденной точке минимума.
При работе с fminsearch нужно учитывать некоторые особенности. Во-первых, функция должна быть гладкой и иметь единственный минимум в заданном диапазоне. Во-вторых, начальное приближение должно быть достаточно близким к точке минимума.
Также существует возможность использовать дополнительные параметры при работе с fminsearch. Например, можно задать ограничения на значения переменных или передать дополнительные параметры в оптимизируемую функцию.
В итоге, работа с fminsearch позволяет эффективно оптимизировать функции и найти минимум заданной функции. Однако важно учитывать особенности данной функции и правильно выбирать начальное приближение.
Задание начального приближения
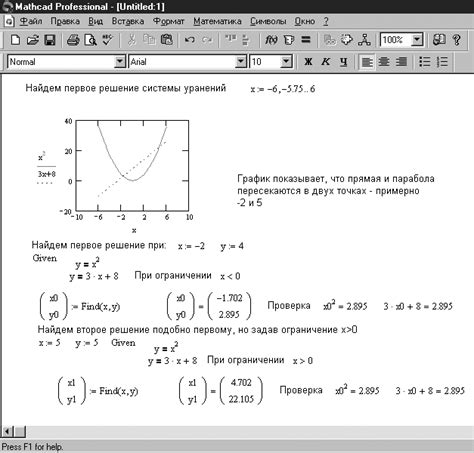
Оптимальное начальное приближение позволяет алгоритму сойтись к наилучшему решению за минимальное количество итераций. При неправильном выборе начального приближения алгоритм может сойтись к локальному минимуму или расходиться.
Существует несколько подходов к выбору начального приближения:
- Экспертный подход: опытный пользователь может задать начальное приближение на основе своих знаний о функции и ее поведении. Например, если известно, что функция имеет единственный минимум, можно задать начальное приближение в этой точке.
- Подбор: можно попробовать различные значения начального приближения и выбрать то, которое дает наилучший результат. Этот подход особенно полезен, если нет достаточного знания о функции.
- Автоматический подбор: некоторые алгоритмы оптимизации могут автоматически подобрать начальное приближение. Например, алгоритмы генетической оптимизации часто используют случайные значения в качестве начального приближения.
Важно помнить, что начальное приближение является лишь отправной точкой, и алгоритм оптимизации самостоятельно ищет наилучшее решение в окрестности этой точки. Правильный выбор начального приближения может значительно ускорить процесс оптимизации и улучшить качество найденного решения.
Определение ограничений

При использовании функции fminsearch для оптимизации параметров модели важно определить ограничения, которые будут применяться к переменным. Ограничения могут быть полезными, чтобы избежать слишком больших или слишком малых значений переменных, которые могут привести к неадекватным результатам или несходимости алгоритма оптимизации.
Для определения ограничений можно использовать несколько подходов:
1. Установка верхней и нижней границы. Для каждой переменной можно задать минимальное и максимальное значение. Например:
bounds = [0, 10; -inf, inf];
В данном примере первой переменной будет установлено ограничение от 0 до 10, а вторая переменная будет без ограничений.
2. Использование ограничений с помощью функции constraint. Этот подход позволяет задать произвольные ограничения, основанные на возможности пользовательской функции. Функция constraint должна принимать входные параметры и возвращать значение, указывающее, удовлетворяет ли текущее значение переменных ограничениям или нет. Например:
function c = constraint(x) if x(1) + x(2) >= 1 c = 1; else c = -1; end end
В данном примере переменные x1 и x2 ограничиваются условием x1 + x2 >= 1. Если это условие выполняется, функция constraint возвращает 1, иначе -1.
Для использования функции constraint в fminsearch достаточно передать ее как входной параметр:
options = optimset('ConstraintTolerance', 1e-6, 'Nonlcon', @constraint);
x = fminsearch(@myfun, x0, options);
Где myfun - оптимизируемая функция, x0 - начальное значение переменных, options - структура с опциями оптимизации.
Определение ограничений позволяет улучшить результаты оптимизации и сделать их более надежными, уверенными и применимыми в реальных задачах.
Установка целевой функции
При установке целевой функции необходимо учитывать следующие аспекты:
1. Формат целевой функции:
Целевая функция должна быть определена в виде отдельной функции или анонимной функции.
2. Входные параметры целевой функции:
Целевая функция может принимать один или несколько входных параметров. Входные параметры могут быть числами, векторами или матрицами.
3. Выходное значение целевой функции:
Целевая функция должна возвращать одно числовое значение, которое будет использоваться для оценки оптимальности текущего решения.
При выборе целевой функции следует учитывать конкретные требования и особенности задачи оптимизации. Целевая функция должна быть связана с целью оптимизации и учитывать все релевантные факторы.
Установка правильной целевой функции является важным шагом при использовании функции оптимизации fminsearch. От выбора и реализации целевой функции зависит точность и эффективность работы алгоритма оптимизации.
Настройка параметров алгоритма

Для эффективного использования функции fminsearch и достижения требуемых результатов, важно правильно настроить параметры её алгоритма оптимизации.
Один из основных параметров алгоритма - это 'MaxIter', который определяет максимальное количество итераций. Установка достаточно большого значения этого параметра может привести к улучшению точности решения, однако также может увеличить время выполнения функции.
Параметр 'TolX' отвечает за критерий сходимости, то есть за то, когда алгоритм должен остановиться. Значение TolX определяет, насколько близко должно быть последнее приближение к оптимуму. Здесь стоит выбирать достаточно малое значение, но не слишком маленькое, чтобы избежать зацикливания.
Еще одним важным параметром является 'TolFun', который отвечает за допустимую погрешность значения функции в оптимальной точке. Если разница между последними приближениями значительно меньше, чем значение 'TolFun', алгоритм считается сходящимся.
Параметр 'Display' определяет уровень отображения информации во время работы алгоритма. Значения этого параметра могут быть: 'off' (ничего не отображать), 'iter' (отображать информацию на каждой итерации) и 'final' (отображать информацию только в конце работы алгоритма).
Пример настройки параметров:
% set options
options = optimset('MaxIter', 1000, 'TolX', 1e-6, 'TolFun', 1e-6, 'Display', 'iter');
% run fminsearch
[x, fval] = fminsearch(@myfun, x0, options);
Грамотная настройка этих параметров позволит более точно и эффективно использовать функцию fminsearch и достигать лучших результатов оптимизации.
Проверка результатов
После выполнения оптимизации с использованием функции fminsearch следует всегда проверять полученные результаты. Даже при использовании хорошо настроенного алгоритма и правильно выбранной функции потерь могут возникнуть случаи, когда найти абсолютно точное решение не удастся.
Одним из способов проверки результатов является повторное вычисление значения целевой функции для найденных оптимальных параметров. Если значение целевой функции близко к нулю или достигает минимального значения, можно считать результатом оптимизации удовлетворительным.
Также полезным может быть анализ визуальных результатов оптимизации. Например, если оптимизация производится для поиска наилучшей аппроксимации кривой, можно построить график и сравнить его с исходными данными. Если аппроксимация соответствует новым данным, можно считать результат оптимизации успешным.
Более объективную оценку результатов можно получить сравнивая параметры найденного оптимального решения с ожидаемыми значениями. Если параметры близки к ожидаемым значениям, можно считать результат оптимизации хорошим.
Однако, не стоит забывать, что результаты оптимизации могут зависеть от выбранного начального приближения и настройки алгоритма. Поэтому рекомендуется проводить несколько запусков оптимизации с разными начальными приближениями и анализировать полученные результаты.
Оптимизация сложных функций

Одним из ключевых моментов при оптимизации сложных функций является правильный выбор начальной точки. Подбор подходящей начальной точки может значительно ускорить процесс оптимизации, поскольку фундаментальная идея fminsearch - перебор в пространстве параметров - может быть более эффективной, если начать с близкой к оптимальной точкой. Оптимальным выбором начальной точки будет набор параметров, который начинает процесс оптимизации вблизи истинного значения параметров.
Кроме выбора начальной точки, при оптимизации сложных функций также важно правильно задать параметры алгоритма оптимизации. Некоторые параметры, которые можно настраивать, включают максимальное количество итераций и допустимую погрешность. Эти параметры должны быть выбраны таким образом, чтобы обеспечить баланс между достижением оптимального результата и временем выполнения.
Для оптимизации сложных функций можно использовать функции обратного вызова, чтобы получить информацию о процессе оптимизации. Они позволяют отслеживать текущие значения параметров и значения функции цели на каждой итерации. Это может быть полезно для анализа и оптимизации процесса оптимизации и принятия дальнейших мер для улучшения его результатов.
Оптимизация сложных функций с помощью fminsearch требует экспериментирования с различными стратегиями и параметрами оптимизации. Часто требуется достаточно времени и терпения для достижения оптимального результата. Однако, правильное использование fminsearch может значительно улучшить процесс оптимизации сложных функций и привести к получению наилучших результатов.
Примеры использования fminsearch

1. Оптимизация параметров модели: fminsearch может использоваться для оптимизации параметров математических моделей. Например, рассмотрим модель экспоненциального роста популяции, где нужно найти оптимальные значения коэффициентов роста и начальной популяции. Fminsearch можно использовать для поиска таких значений, чтобы минимизировать расхождение между моделью и экспериментальными данными.
2. Настройка алгоритмов машинного обучения: fminsearch может быть полезен для настройки параметров алгоритмов машинного обучения, таких как нейронные сети или метод опорных векторов. Путем минимизации функционала ошибки можно подобрать оптимальные значения весовых коэффициентов или настроек алгоритмов для достижения лучшей производительности.
3. Решение задач оптимизации: fminsearch может использоваться для решения различных задач оптимизации. Например, задачу построения портфеля инвестиций можно решить с помощью fminsearch, где нужно найти оптимальное соотношение активов для максимизации ожидаемой доходности при заданном уровне риска.
4. Программирование алгоритмов: fminsearch может быть использован для программирования различных алгоритмов, таких как алгоритмы поиска пути, оптимального распределения ресурсов и т. д. Путем оптимизации функционала можно найти оптимальные значения параметров алгоритмов и улучшить их эффективность.
5. Инженерные расчеты: fminsearch может быть использован для решения различных инженерных задач, таких как оптимизация структуры материалов, оптимальное распределение энергии или максимизация эффективности системы. Fminsearch позволяет найти оптимальные значения параметров, удовлетворяющие заданным ограничениям и требованиям.
Таким образом, fminsearch предоставляет эффективный инструмент для решения различных задач оптимизации и оптимизации параметров моделей в науке и инженерии.