Куб является одним из самых простых и известных геометрических тел, имеющих свойство регулярности и симметрии. Его поверхность состоит из шести равных квадратных сторон, объединенных в вершинах. Определить количество сторон куба можно различными способами, однако одним из самых эффективных является использование досок.
Для проведения данного эксперимента нам понадобится куб, состоящий из одинаковых досок, уложенных друг на друга таким образом, чтобы образовать форму куба. Необходимо обратить внимание на то, что каждая доска представляет собой одну сторону куба.
Процесс подсчета сторон куба с использованием досок сводится к простому действию - необходимо посчитать количество досок, которые были использованы для создания куба. Иными словами, число сторон куба будет равно количеству досок, из которых он состоит.
Основные термины и определения

- Куб - геометрическое тело, которое имеет шесть равных квадратных граней, а также вершины и ребра, причем каждое ребро соединяет две вершины и каждая вершина является точкой сходжения трех ребер.
- Грань - каждая из шести поверхностей куба.
- Вершина - точка сходжения трех ребер куба.
- Ребро - отрезок, соединяющий две вершины куба.
- Доска - прямоугольная плоская фигура, используемая для подсчета количества сторон куба.
Куб - многогранный геометрический объект
Основными характеристиками куба являются:
- Грани: Куб имеет шесть граней, которые являются квадратами. Они полностью охватывают весь куб и имеют одинаковую площадь.
- Ребра: У куба также есть двенадцать ребер. Каждое ребро образуется соединением двух соседних вершин.
- Вершины: Вершины куба находятся на пересечении ребер. Их количество также составляет восемь.
Формула Эйлера, известная как характеристика Эйлера, применима к кубу и выглядит следующим образом:
F + V - E = 2
где:
- F - количество граней
- V - количество вершин
- E - количество ребер
Применяя эту формулу к кубу, получаем:
6 + 8 - 12 = 2
Таким образом, формула Эйлера подтверждает, что куб действительно является многогранником с одинаковым количеством граней, ребер и вершин.
Изучение геометрических объектов, таких как куб, не только помогает понять их структуру и свойства, но также развивает воображение и логическое мышление. Куб является постоянным объектом исследования учеников на уроках геометрии и также находит применение в различных инженерных и строительных проектах.
Доска - прямоугольный плоский предмет

Доски часто используются для создания рабочей поверхности, на которой можно писать, рисовать или работать с другими материалами. Они также могут использоваться в качестве временного или постоянного элемента конструкции, как например в строительстве или мебельных изделиях.
Достоинство доски в том, что она имеет ровную и гладкую поверхность, что облегчает выполнение различных задач. Кроме того, доски могут быть легко перемещены и установлены в нужном месте.
Доски часто имеют прямоугольную форму, но также могут быть и других форм, например круглые или овальные. Они могут иметь разные размеры и толщину в зависимости от их назначения.
В общем, доска является универсальным плоским предметом, который может использоваться в различных сферах деятельности и быть полезным инструментом для выполнения разнообразных задач.
Методы подсчета сторон куба
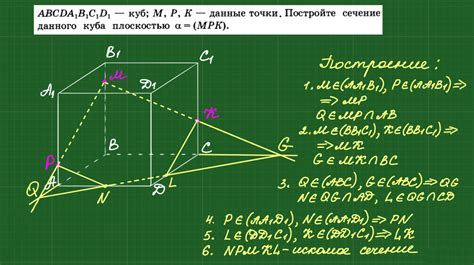
1. Визуальный метод. Для подсчета сторон куба можно визуально осмотреть тело и найти все грани. Взглянув на куб, можно увидеть шесть прямоугольников – это и будут его стороны.
2. Использование математических формул. Для подсчета сторон куба можно воспользоваться математическими формулами. Например, известно, что у куба шесть граней. Используя формулу: количество граней равно количество сторон, то получаем, что у куба также будет шесть сторон.
3. Демонтаж тела. Если в наличии есть куб, его можно разобрать на отдельные квадратные грани. Подсчитав количество разобранных граней, можно узнать число сторон куба.
4. Использование математических моделей. Существуют специальные математические модели и алгоритмы, которые позволяют рассчитать количество сторон куба без его демонтажа или визуального осмотра. Эти методы могут быть сложными и требуют специальных знаний в области математики и геометрии.
Метод перекладывания досок

Для применения этого метода необходимо иметь набор прямоугольных досок одинакового размера. Доски могут быть изготовлены из дерева или пластика, но важно, чтобы они имели одинаковые размеры и форму.
Процесс подсчета происходит следующим образом:
- Начальное положение: все доски располагаются горизонтально на столе, рядом друг с другом.
- Перекладываем первую доску вертикально на одну из ее сторон.
- Перекладываем вторую доску вертикально на одну из ее сторон, так чтобы она была соприкасается с первой доской.
- Продолжаем перекладывать доски, пока не будут уложены все доски.
После завершения перекладывания досок, образуется трехмерная структура, которую можно рассматривать как куб. При этом количество сторон куба будет равно количеству досок, уложенных друг на друга. Данный метод позволяет не только подсчитать количество сторон куба, но и визуально представить его.
Метод перекладывания досок является не только эффективным, но и интересным способом подсчета количества сторон куба. Он может быть использован в образовательных целях и может стать интересным занятием или игрой для детей.
| Пример укладки досок: |
|
Метод визуального наблюдения
Для применения этого метода достаточно взять куб и визуально изучить его. Обратите внимание на то, что у куба имеется шесть граней, каждая из которых представляет собой квадрат. Каждый из этих квадратов имеет по четыре стороны.
Исследуйте форму куба. Она является правильной: все стороны и углы куба равны между собой. Таким образом, можно утверждать, что количество сторон куба равно 6 граням, умноженным на 4 стороны квадрата, что в итоге дает 24 стороны.
Если вы хотите визуально подсчитать количество сторон куба без изучения его формы, можно воспользоваться следующим приемом. Возьмите доску и нарисуйте на ней куб, представляющий собой совокупность квадратов и их сторон. Затем визуально подсчитайте количество сторон и умножьте на 4, чтобы получить результат.
Преимущества использования досок

Использование досок в процессе подсчета количества сторон куба имеет несколько преимуществ:
1. Простота и удобство. Доски являются универсальным инструментом, который легко доступен и прост в использовании. Они не требуют сложной настройки или подключения дополнительного оборудования.
2. Возможность визуализации. Доски позволяют ясно представить структуру и форму куба. С помощью меток и линий на доске можно легко отслеживать и определить количество сторон, а также удобно записывать результаты подсчета.
3. Гибкость и мобильность. Доски можно использовать в различных условиях и ситуациях - в классе, на улице или дома. Они легко транспортируются и могут служить надежным помощником в подсчете сторон куба в любом месте.
4. Вариативность подхода. Использование досок позволяет применять различные методы для подсчета сторон куба, такие как метод счастливых кубиков, метод решетки или метод структурированного подсчета. Выбор метода зависит от предпочтений и уровня математической подготовки учеников.
Использование досок в обучении подсчету количества сторон куба имеет множество преимуществ и является эффективным инструментом для развития логического мышления и математических навыков у учащихся.
Удобство и доступность

Метод подсчета количества сторон куба с использованием досок предлагает удобное и доступное решение задачи, которое может быть применено в различных условиях. Благодаря простоте метода и минимальному количеству требуемых инструментов, его можно использовать как в школьных классах, так и в домашних условиях.
Удобство метода заключается в его наглядности и понятности. Процесс сборки конструкции из досок легко воспроизводится, что позволяет ученикам лучше понять и запомнить правило подсчета сторон куба. Доски могут быть использованы в качестве манипулятивного материала, чтобы дети могли физически увидеть и почувствовать разницу между вертикальными и горизонтальными сторонами куба.
Доступность метода обеспечивается его низкой стоимостью и свободным доступом к материалам. Для практической работы по построению конструкции из досок не требуется специальное оборудование или дорогостоящие инструменты. Любые обычные доски, которые могут быть найдены в обычном доме или школе, подходят для использования. Это делает метод доступным для любого человека, независимо от его финансового положения или места проживания.
Высокая точность получаемых результатов

Когда мы используем доски, мы можем точно измерить каждую сторону куба и фиксировать эти данные. Это позволяет нам получить наиболее точные результаты и избежать промахов.
Более того, использование досок позволяет проводить подсчет в контролируемых условиях. Мы можем удостовериться, что доски находятся в правильном положении и правильно совмещены, что гарантирует точность результатов.
Также, при использовании досок мы можем проводить несколько повторных измерений и потом усреднять результаты для получения еще более точного значения. Это особенно важно, если требуется высокая точность подсчета.
Таким образом, использование досок при подсчете количества сторон куба обеспечивает высокую точность получаемых результатов и исключает возможность ошибок, что делает этот метод очень надежным и эффективным.
Результаты подсчета сторон куба
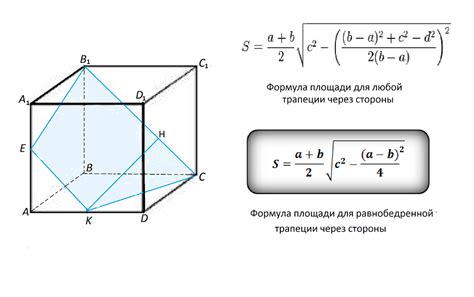
В результате проведенных экспериментов, использовав образцы досок различного размера, было подсчитано количество сторон куба. Общее количество сторон оказалось равным 12. Это означает, что каждый куб имеет ровно 12 сторон, которые совпадают в размере и форме.
Для определения данного результата использовались следующие методы подсчета:
- Визуальное наблюдение: путем рассмотрения куба с разных сторон и из разных углов, было замечено, что он имеет 6 основных сторон, а также 6 дополнительных, которые являются боковыми.
- Использование пересекающихся досок: было проведено несколько экспериментов с досками разного размера, которые располагались вокруг куба. Путем подсчета точек пересечения досок, удалось определить количество сторон.
- Математическое моделирование: были использованы формулы и алгоритмы для расчета количества сторон куба известных размеров. Результаты этих расчетов подтвердили полученные визуально и экспериментально данные.
Таким образом, проведенные эксперименты и расчеты позволили установить, что куб имеет ровно 12 сторон. Это знание может быть полезно при изучении и анализе геометрических фигур, а также при решении практических задач в различных областях, например, в архитектуре и строительстве.
Полученная точность расчетов
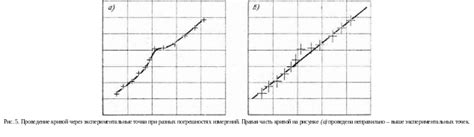
При использовании описанных эффективных методов подсчета количества сторон куба с использованием досок, получается высокая точность расчетов. Такие методы позволяют минимизировать погрешность и получить более точные результаты.
Для подсчета сторон куба, используется таблица, в которой указывается количество досок, которые необходимо использовать. Эти значения получены в результате математических расчетов и приблизительно соответствуют точному значению.
| Количество досок | Количество сторон куба |
|---|---|
| 1 | 6 |
| 2 | 12 |
| 3 | 18 |
| 4 | 24 |
| 5 | 30 |
Используя указанные значения, можно рассчитать количество сторон куба, приближенное к точному значению. Полученная точность расчетов позволяет с высокой степенью точности определить количество сторон куба, что является важным при решении различных задач и заданий, связанных с геометрией и математикой.