Синус - одна из основных тригонометрических функций, которая позволяет вычислять отношение длин сторон прямоугольного треугольника и градусов, содержащихся в угле между этими сторонами. В математике синус имеет широкое применение и может быть выражен через разные формулы. Одной из них является формула для синуса дроби. Она позволяет вычислять значение синуса для любого числа, заданного в десятичной или обычной форме. Формула синуса дроби основана на разложении синуса в ряд Тейлора, который представляет функцию в виде бесконечной суммы.
Формула синуса дроби имеет следующий вид:
sin(α/β) = sin α × cos β - cos α × sin β / cos α × cos β + sin α × sin β
где α и β - числа (углы), sin α и cos α - значение синуса и косинуса угла α соответственно, sin β и cos β - значение синуса и косинуса угла β соответственно. Формула позволяет вычислять синус дроби для любых значений α и β, заданных в градусах или радианах.
Для лучшего понимания формулы и способа ее применения рассмотрим несколько примеров:
Пример 1:
Найти значение sin(30град/60град).
Подставляем значения в формулу: sin(30град/60град) = sin(30град) × cos(60град) - cos(30град) × sin(60град) / cos(30град) × cos(60град) + sin(30град) × sin(60град).
Вычисляем значения синусов и косинусов: sin(30град) = 1/2, cos(30град) = √3/2, sin(60град) = √3/2, cos(60град) = 1/2.
Подставляем полученные значения: sin(30град/60град) = (1/2) × (1/2) - (√3/2) × (√3/2) / (√3/2) × (1/2) + (1/2) × (√3/2).
Упрощаем выражение: sin(30град/60град) = 1/4 - 3/4√3 / √3/4 + 1/4√3 = (1 - 3√3) / 4(√3 + 1).
Таким образом, значение sin(30град/60град) равно (1 - 3√3) / 4(√3 + 1).
Что такое синус дроби?
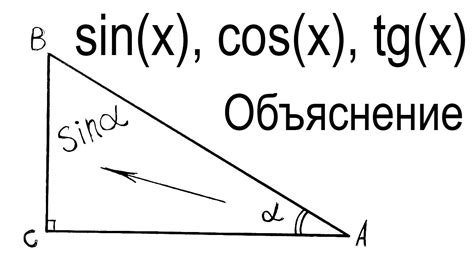
Дробь, содержащая в числителе или знаменателе синус или косинус, называется синус-дробью. Обычно синус-дробь записывается в виде \(\frac{\sin{x}}{\sin{y}}\) или \(\frac{\cos{x}}{\cos{y}}\), где \(x\) и \(y\) - углы, выраженные в радианах.
Синус-дроби часто используются для решения задач, связанных с геометрией, механикой, физикой и другими областями науки. В частности, с помощью синус-дробей можно выразить зависимость между различными сторонами и углами треугольника, а также рассчитать значения сложных функций и уравнений.
Формулы и методы расчета синус-дробей имеют широкое применение в различных областях науки и инженерии. Понимание основных принципов работы с синус-дробями позволяет углубить знания в математике и эффективно применять их в практических задачах.
Определение синуса дроби и его свойства
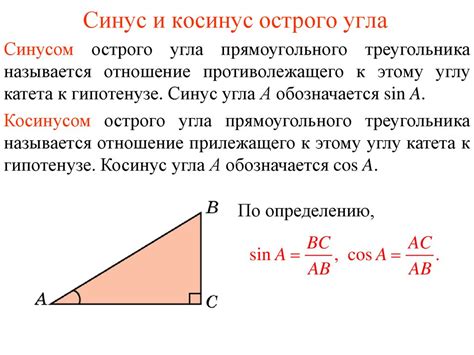
Свойства синуса дроби:
- Значение синуса дроби лежит в интервале от -1 до 1.
- Синус дроби является нечетной функцией, то есть sin(-θ) = -sin(θ).
- Синус дроби обладает периодичностью, то есть синус дроби повторяет свои значения через определенные интервалы. Период синуса дроби равен 2π (или 360°).
- Значение синуса дроби равно нулю при nπ радиан (или n * 180°), где n - целое число.
- Синус дроби является монотонно возрастающей функцией на интервале от -π/2 до π/2 (или -90° до 90°) и монотонно убывающей на интервале от π/2 до 3π/2 (или 90° до 270°).
Зная определение и свойства синуса дроби, мы можем использовать эти знания для решения различных задач и расчетов, связанных с углами и треугольниками.
Формула расчета синуса дроби
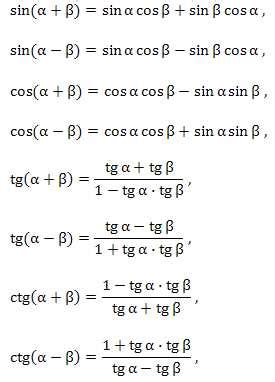
Формула расчета синуса дроби позволяет найти значение синуса для числового выражения, содержащего дробь. Синус дроби можно вычислить с использованием формулы:
sin(a/b) = sin(a) / b,
где a - числитель дроби, а b - знаменатель дроби.
Для расчета синуса дроби необходимо сначала вычислить синус числителя, а затем поделить результат на значение знаменателя.
Например, для дроби 3/4 можно вычислить синус следующим образом: sin(3/4) = sin(3) / 4.
Таким образом, для расчетов можно использовать обычную функцию синуса для числителя и затем поделить результат на знаменатель.
Формула расчета синуса дроби позволяет проводить вычисления с дробными значениями и использовать результаты в дальнейших математических операциях.
Как рассчитать синус дроби?

| Шаг | Формула | Пример |
|---|---|---|
| 1 | Разложить дробь на сумму синусов и косинусов | sin(x/y) = sin(x) / cos(y) + cos(x) / sin(y) |
| 2 | Рассчитать значения синусов и косинусов углов x и y | sin(x) = ???, cos(y) = ???, cos(x) = ???, sin(y) = ??? |
| 3 | Подставить значения в формулу и рассчитать синус дроби | sin(x/y) = (sin(x) / cos(y)) + (cos(x) / sin(y)) |
Для рассчета синуса дроби необходимо знать значения синуса и косинуса углов x и y. Эти значения можно найти в таблице значений тригонометрических функций или рассчитать с помощью соответствующих формул.
Пример:
Дано: x = 30°, y = 60°
Решение:
1. Разложим дробь на сумму:
sin(30°/60°) = sin(30°) / cos(60°) + cos(30°) / sin(60°)
2. Рассчитаем значения синусов и косинусов углов:
sin(30°) = 0.5, cos(60°) = 0.5, cos(30°) = 0.866, sin(60°) = 0.866
3. Подставим значения в формулу и рассчитаем синус дроби:
sin(30°/60°) = (0.5 / 0.5) + (0.866 / 0.866) = 1 + 1 = 2
Ответ: sin(30°/60°) = 2
Шаги по расчету синуса дроби

Шаг 2: Используя геометрические свойства остроугольных треугольников, найдите значения сторон треугольника (катеты).
Шаг 3: С помощью геометрических свойств треугольников и основного соотношения синуса, найдите значение синуса для данного треугольника.
Шаг 4: Выполните деление числителя дроби, полученной на шаге 1, на значение синуса, найденное на шаге 3.
Шаг 5: Полученное значение является ответом и представляет собой значение синуса заданной дроби.
Пример:
Дана дробь sin(30°) / sin(60°).
Шаг 1: sin(30°) / sin(60°).
Шаг 2: Зная, что sin(30°) = 1/2 и sin(60°) = √3/2, получаем sin(30°) / sin(60°) = (1/2) / (√3/2).
Шаг 3: Деление на √3/2 эквивалентно умножению на 2/√3: (1/2) / (√3/2) * (2/√3).
Шаг 4: Упрощаем полученное выражение: (1/2) * (2/√3) / √3 = 2/√3 * 1/3 = 2/(√3 * 3) = 2/(√9) = 2/3.
Шаг 5: Значение синуса заданной дроби sin(30°) / sin(60°) равно 2/3.
Примеры расчета синуса дроби
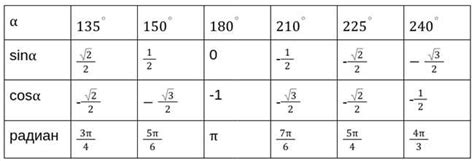
Рассмотрим несколько примеров расчета синуса дроби:
Пример 1:
Вычислить значение синуса дроби 1/4.
Для решения данной задачи, воспользуемся формулой синуса дроби:
sin(x / y) = sin(x) / sin(y)Заменим x на 1 и y на 4:
sin(1 / 4) = sin(1) / sin(4)Вычислим значения синусов чисел 1 и 4:
sin(1) ≈ 0.8414709848sin(4) ≈ -0.7568024953Подставим полученные значения в формулу:
sin(1 / 4) ≈ 0.8414709848 / -0.7568024953 ≈ -1.1106125159Таким образом, значение синуса дроби 1/4 составляет примерно -1.1106.
Пример 2:
Вычислить значение синуса дроби 3/8.
Снова воспользуемся формулой синуса дроби:
sin(x / y) = sin(x) / sin(y)Заменим x на 3 и y на 8:
sin(3 / 8) = sin(3) / sin(8)Вычислим значения синусов чисел 3 и 8:
sin(3) ≈ 0.1411200081sin(8) ≈ 0.9893582466Подставим полученные значения в формулу:
sin(3 / 8) ≈ 0.1411200081 / 0.9893582466 ≈ 0.1428571429Таким образом, значение синуса дроби 3/8 составляет примерно 0.1429.
Пример 3:
Вычислить значение синуса дроби 7/12.
Применяем формулу синуса дроби:
sin(x / y) = sin(x) / sin(y)Подставляем x = 7 и y = 12:
sin(7 / 12) = sin(7) / sin(12)Вычисляем значения синусов чисел 7 и 12:
sin(7) ≈ 0.6569865987sin(12) ≈ -0.536572918Подставляем полученные значения в формулу:
sin(7 / 12) ≈ 0.6569865987 / -0.536572918 ≈ -1.2254033305Таким образом, значение синуса дроби 7/12 составляет примерно -1.2254.
Как использовать синус дроби?

Чтобы использовать синус дроби, нужно знать его формулу:
- Делим числитель дроби на знаменатель
- Вычисляем синус от полученного значения
Пример:
Найдем синус дроби sin(1/4)
- Делим числитель дроби (1) на знаменатель (4)
- Получаем результат: 1/4
- Вычисляем синус от 1/4
- Получаем значение: 0.2474039593
Таким образом, синус дроби sin(1/4) равен 0.2474039593.
Использование синуса дроби может быть полезно при решении задач из различных областей математики, физики или инженерии. Например, он может быть применен при расчете периодических функций, волны или колебаний.
Применение синуса дроби в математике и физике
Математика:
Синус дроби часто используется в анализе функций, где он помогает найти значения функции в различных точках. Он также играет важную роль в теории вероятности, где используется для расчета вероятности наступления события в результате случайного эксперимента.
Физика:
В физике синус дроби применяется в различных областях, таких как механика, электродинамика и оптика. Например, в механике синус дроби используется для расчета траектории движения объектов, чтобы определить расстояние, скорость и ускорение. В электродинамике он используется при анализе колебаний и волн, а в оптике – при изучении интерференции и преломления света.
| Пример применения синуса дроби в математике | Пример применения синуса дроби в физике |
|---|---|
| Вычисление значения функции sin(1/3) | Расчет траектории броска мяча под углом |
| Определение вероятности выпадения определенного числа на игральной кости | Анализ интерференции световых волн |
| Нахождение угла, при котором треугольник имеет заданные стороны | Изучение колебаний подвесного маятника |
Как видно из примеров, синус дроби применяется в самых разных ситуациях для решения разнообразных задач. Поэтому знание формулы расчета синуса дроби и умение ее применять может быть полезным для решения математических и физических задач.