Параллелепипед – это геометрическое тело, которое имеет три пары параллельных граней. Он также называется прямоугольным параллелепипедом, так как все его грани – прямоугольники. Ученики пятых классов рано или поздно сталкиваются с вопросом: сколько же граней у данной фигуры?
Ответ на этот вопрос достаточно прост. Чтобы найти количество граней у параллелепипеда, требуется знать, что у него есть 6 граней. Каждая из граней - прямоугольник. Параллелепипед имеет 3 пары параллельных сторон, которые образуют 6 прямоугольников.
Поэтому, если у вас есть параллелепипед, вам необходимо только посчитать количество прямоугольников, чтобы узнать, сколько у него граней. И помните - параллелепипед может иметь только 6 граней!
Что такое параллелепипед? Простое объяснение для школьников

В своей простейшей форме, параллелепипед очень похож на обычную кубическую коробку, которую можно встретить в повседневной жизни. Он имеет шесть сторон, все из которых являются прямоугольниками. Каждая сторона параллелепипеда называется гранью.
У параллелепипеда всего 6 граней: три пары параллельных сторон. Грани параллелепипеда - это плоские поверхности, которые его ограничивают, подобно стенкам кубической коробки. Грани помогают нам визуализировать форму параллелепипеда и определять его свойства.
Важным свойством всех граней параллелепипеда является то, что они прямоугольники - это значит, что у каждой грани есть две параллельные стороны и углы, равные 90 градусам. Благодаря этим свойствам, параллелепипед является удобной фигурой для изучения геометрии и математических концепций.
Теперь, когда вы знаете, что такое параллелепипед и что такое его грани, вы можете решать задачи и играть с этим удивительным геометрическим объектом!
Как выглядит параллелепипед и как его различить?
У параллелепипеда все грани параллельны парам противоположных граней. Все ребра параллелепипеда параллельны и одинаковой длины. Также все углы между парами граней параллелепипеда прямые.
Параллелепипеды различаются формой и размерами своих граней. Они могут быть вытянутыми в длину или сжатыми в ширину или высоту. Также они могут иметь различную форму граней, например, квадратные или прямоугольные.
Чтобы различить параллелепипеды, важно обратить внимание на соотношение сторон и форму каждой грани. Например, если все грани квадратные, то это будет куб. Если же все грани прямоугольные, то это будет прямоугольный параллелепипед.
Теперь, когда вы знаете как выглядит параллелепипед и как его различить, вы сможете легко определить количество его граней и классифицировать эту фигуру точно!
Определение граней и их количество в параллелепипеде
Чтобы определить количество граней в параллелепипеде, нужно рассмотреть его структуру. Параллелепипед имеет три парами параллельных сторон, каждая из которых является гранью. Следовательно, общее количество граней равно сумме граней каждой пары. Учитывая, что каждая пара сторон имеет две грани, общее количество граней в параллелепипеде равно 2 * 3 = 6.
Примеры граней параллелепипеда:
- Грань верхняя - верхняя поверхность параллелепипеда.
- Грань нижняя - нижняя поверхность параллелепипеда.
- Грань передняя - передняя поверхность параллелепипеда.
- Грань задняя - задняя поверхность параллелепипеда.
- Грань правая - правая боковая поверхность параллелепипеда.
- Грань левая - левая боковая поверхность параллелепипеда.
Таким образом, параллелепипед имеет шесть граней, которые могут быть названы в соответствии с их расположением и ориентацией в пространстве.
Простая формула для подсчета количества граней
Формула для подсчета количества граней у параллелепипеда:
G = 2(a * b + a * c + b * c)
Где:
- G - количество граней;
- a, b, c - длины сторон параллелепипеда.
Для простого способа подсчета граней нужно умножить сумму попарных произведений длин сторон на 2.
Например, если у нас есть параллелепипед со сторонами длиной 3, 4 и 5, то количество граней будет:
G = 2(3 * 4 + 3 * 5 + 4 * 5) = 2(12 + 15 + 20) = 2 * 47 = 94
Таким образом, параллелепипед с указанными сторонами будет иметь 94 грани.
Интересные факты о параллелепипеде, связанные с гранями:

1. Параллелепипед имеет 6 граней. Как и все прямоугольные призмы, у него есть две пары параллельных граней и четыре пары прямых ребер, соединяющих соответствующие точки параллельных граней.
2. Все грани параллелепипеда являются прямоугольниками. Это означает, что все углы каждой грани равны 90 градусам.
3. Параллелепипед - одно из основных геометрических тел, используемых в архитектуре и строительстве. Он широко применяется для создания прямоугольных комнат, коробок, ящиков и многих других объектов.
4. Плоскости граней параллелепипеда параллельны друг другу. Они не пересекаются и не пересекаются с ребрами или углами.
5. Параллелепипед имеет 12 ребер, 8 вершин и 24 ребра. Каждый ребер соединяет две вершины параллелепипеда.
6. Грани параллелепипеда могут быть раскрашены в разные цвета, чтобы создать интересный и разнообразный дизайн.
7. Длины граней параллелепипеда могут быть различными. Однако, внутренние углы все равны 90 градусам, независимо от размера граней.
8. Параллелепипед является трехмерным объектом, что означает, что он имеет длину, ширину и высоту.
| Грани | Углы | Ребра |
|---|---|---|
| 6 | 90° | 12 |
Зачем нужно знать количество граней у параллелепипеда?
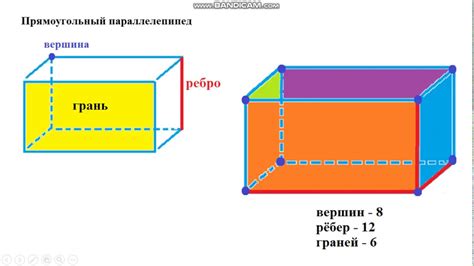
Понимание количества граней у параллелепипеда имеет важное значение в геометрии и других областях науки и техники. Знание количества граней помогает нам определить форму и свойства объекта. Вот несколько причин, почему важно знать количество граней у параллелепипеда:
1. Геометрия и пространство Знание количества граней помогает нам понять структуру и форму объекта в трехмерном пространстве. Гранями параллелепипеда являются его стороны и края, которые определяют его объем и площадь поверхности. Это позволяет нам классифицировать и сравнивать различные формы и структуры объектов. | |
2. Различные области науки и техники Знание количества граней у параллелепипеда имеет практическое применение в различных областях науки и техники. Например, в архитектуре и строительстве знание количества граней помогает инженерам и архитекторам моделировать и проектировать здания и сооружения. | |
3. Улучшение математического мышления Изучение геометрии и понимание форм и структур объектов помогает развить математическое мышление. Работа с гранями параллелепипеда и других геометрических фигур развивает логическое и абстрактное мышление, а также помогает улучшить навыки решения задач и проблемного мышления. |
Это всего лишь несколько примеров того, почему важно знать количество граней у параллелепипеда. Без этого знания мы не смогли бы понять форму и свойства многих объектов в окружающем нас мире.
Задачи и упражнения для тренировки расчета граней

1. Решите следующую задачу: у параллелепипеда есть 6 граней. Один из углов параллелепипеда имеет площадь 12 квадратных сантиметров. Найдите площадь одной грани параллелепипеда.
2. Вычислите площадь грани параллелепипеда, если известно, что площадь всей поверхности параллелепипеда равна 96 квадратных сантиметров, а количество граней равно 6.
3. Рассчитайте количество граней у параллелепипеда, если общая площадь всех граней равна 120 квадратных сантиметров, а площадь одной грани равна 20 квадратных сантиметров.
4. Найдите площадь грани параллелепипеда, если его общая площадь равна 200 квадратных сантиметров, а количество граней равно 6.
5. Решите задачу: у параллелепипеда есть 8 граней, общая площадь которых составляет 160 квадратных сантиметров. Найдите площадь одной грани параллелепипеда.
6. Параллелепипед имеет 6 граней с общей площадью 300 квадратных сантиметров. Найдите количество граней параллелепипеда.
Примеры с решениями задач, связанных с гранями параллелепипеда
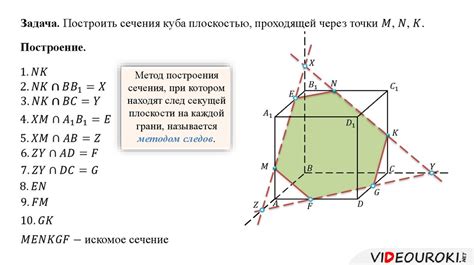
Давайте рассмотрим несколько примеров задач, связанных с гранями параллелепипеда, и их решений.
Пример 1:
Найдите количество граней у параллелепипеда, если у него 4 прямоугольные грани в основании и 2 прямоугольные грани по бокам.
Решение:
У параллелепипеда есть две грани внешние - одна на верхушке и одна на нижней стороне. Эти две грани называются верхней и нижней гранями. Каждая из этих двух граней образована перемножением длинных сторон параллелепипеда - длина и ширина, и содержит по два прямоугольника. Таким образом, верхняя и нижняя грани вместе составляют 4 прямоугольника.
Также у параллелепипеда есть четыре вертикальные грани. Они образованы перемножением длины и высоты параллелепипеда, а каждая грань состоит из двух прямоугольников. Таким образом, четыре вертикальные грани также составляют 4 прямоугольника.
Итак, общее количество граней у параллелепипеда - это сумма граней верхней, нижней и вертикальных сторон, то есть 4 + 4 = 8 граней.
Пример 2:
Параллелепипед имеет 6 граней, каждая из которых является прямоугольником. Известно, что все прямые углы на гранях параллелепипеда равны между собой. Найдите количество граней, у которых все углы равны 90 градусов.
Решение:
Пусть количество граней со всеми углами равными 90 градусам равно Х.
У параллелепипеда всего 6 граней, поэтому известно, что Х + количество граней с неравными углами = 6.
Поскольку все прямые углы параллелепипеда равны между собой, грани параллелепипеда делятся на две группы - грани с прямыми углами и грани с неравными углами. В нашем случае, количество граней с неравными углами равно 0, так как все углы равны 90 градусам.
Таким образом, Х + 0 = 6, откуда Х = 6.
Итак, количество граней с прямыми углами равно 6.
Пример 3:
Найдите количество граней у параллелепипеда, если у него 12 ребер и 8 вершин.
Решение:
У параллелепипеда есть 8 вершин, каждая из которых соединена с 3 ребрами. Таким образом, общее количество ребер параллелепипеда равно 8 * 3 = 24 ребра.
Однако, каждое ребро принадлежит двум граням, поэтому общее количество ребер у граней, составляющих параллелепипед, равно половине от общего количества ребер - 24 / 2 = 12 ребер.
Таким образом, общее количество граней у параллелепипеда равно 12 граней.
Это лишь некоторые примеры задач, связанных с гранями параллелепипеда. Надеемся, что эти примеры помогут вам лучше понять и запомнить основные понятия и свойства граней параллелепипеда.


