Критерий Фишера – один из основных статистических методов, используемых для сравнения различных групп данных. Для его применения необходимо знать количество степеней свободы. Количество степеней свободы является важным показателем меры свободы выборки, и его корректное определение является неотъемлемой частью проведения анализа по критерию Фишера.
Количество степеней свободы в критерии Фишера зависит от двух факторов: числа групп и размеров выборок в каждой группе. Чтобы рассчитать количество степеней свободы, необходимо вычислить количество степеней свободы для каждой группы и затем сложить полученные значения. Такой подход позволяет получить общее количество степеней свободы, учитывающее все группы и размеры выборок.
Чтобы вычислить количество степеней свободы для каждой группы, необходимо знать размер выборки в данной группе. Формула для определения количества степеней свободы группы имеет вид: степени свободы = размер выборки - 1. После того как получены значения для каждой группы, их нужно просуммировать для определения общего количества степеней свободы критерия Фишера.
Количество степеней свободы критерия Фишера
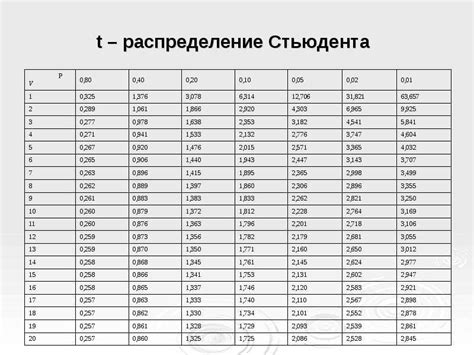
Количество степеней свободы в критерии Фишера зависит от количества наблюдений и количества групп. Если у нас есть две группы, то количество степеней свободы для числителя равно количеству групп минус один, а для знаменателя – общее количество наблюдений минус количество групп.
Например, если у нас есть две группы по 30 наблюдений каждая, то количество степеней свободы для числителя будет равно 2 минус 1, то есть 1, а для знаменателя – 60 минус 2, то есть 58. Если у нас есть три группы по 20 наблюдений каждая, то количество степеней свободы для числителя будет равно 3 минус 1, то есть 2, а для знаменателя – 60 минус 3, то есть 57.
Что такое критерий Фишера?
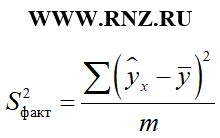
Основная идея критерия Фишера заключается в сравнении двух оценок дисперсий: межгрупповой и внутригрупповой. Межгрупповая дисперсия характеризует различия между средними значениями различных групп, тогда как внутригрупповая дисперсия отражает вариацию показателей внутри каждой из групп.
Для вычисления критерия Фишера необходимо знать значения этих двух оценок дисперсий и количество степеней свободы для каждой из них. Количество степеней свободы представляет собой параметр, который указывает на число наблюдений, которые могут быть использованы для оценки дисперсии.
В критерии Фишера количество степеней свободы для межгрупповой дисперсии обозначается как df1, а для внутригрупповой - как df2. Они вычисляются на основе количества групп данных и числа наблюдений в каждой группе.
При применении критерия Фишера вычисляется наблюдаемое значение F-критерия, которое сравнивается с критическим значением из F-таблицы. Если наблюдаемое значение F-критерия больше критического значения, то различие между средними значениями групп является статистически значимым.
| Группа | Количество наблюдений |
|---|---|
| Группа 1 | 50 |
| Группа 2 | 60 |
В данном примере для критерия Фишера мы будем иметь две группы данных (группа 1 и группа 2) с количеством наблюдений соответственно 50 и 60. Необходимо вычислить оценки дисперсий, количество степеней свободы и провести статистическую проверку различий между средними значениями групп.
Как вычислить количество степеней свободы критерия Фишера?
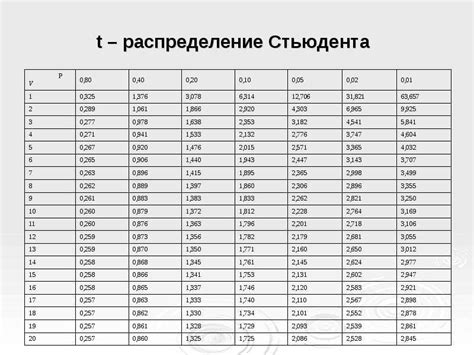
- Числа степеней свободы числителя и знаменателя.
- Тип теста: односторонний или двусторонний.
Для вычисления количества степеней свободы критерия Фишера вам понадобится формула, которая различается в зависимости от тестируемой гипотезы:
- Для одностороннего теста:
df1 = k - 1(степени свободы числителя)
df2 = n - k(степени свободы знаменателя) - Для двустороннего теста:
df1 = k - 1(степени свободы числителя)
df2 = n - k(степени свободы знаменателя)
Где:
k- число групп или факторов в анализе.n- общее число наблюдений или данных.
На основе формулы вы можете вычислить количество степеней свободы для вашего теста.
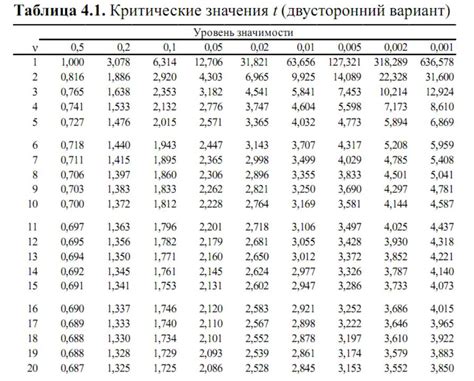
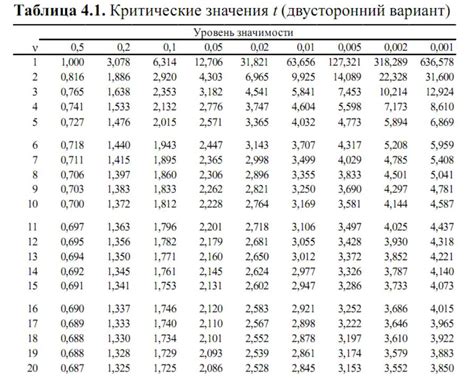
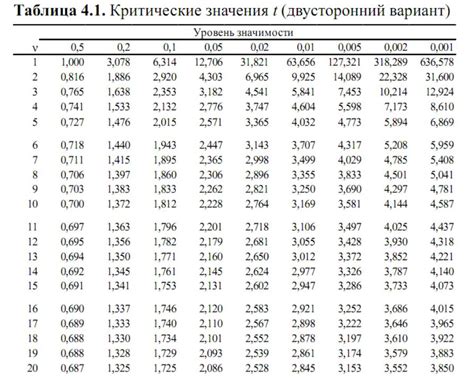
Количество степеней свободы влияет на критическое значение статистики Фишера и на оценку статистической значимости теста. Более высокое количество степеней свободы даёт более точные результаты. Зная количество степеней свободы, вы можете использовать таблицы критических значений для определения критической области и принятия решения о статистической значимости результатов.
Зачем нужно знать количество степеней свободы критерия Фишера?
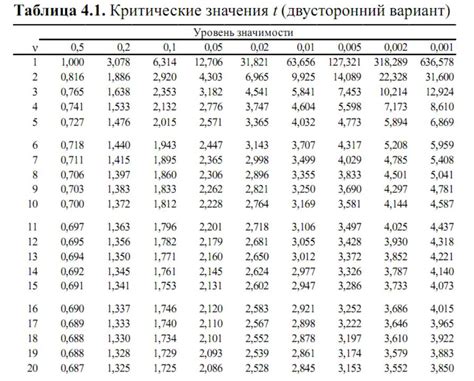
Количество степеней свободы критерия Фишера является играющим ключевую роль в расчетах и интерпретации результатов. Степени свободы представляют собой число независимых точек данных, которые используются в анализе. Чем больше степеней свободы, тем более достоверными и репрезентативными будут полученные результаты.
Как использовать количество степеней свободы критерия Фишера при анализе данных?
Для использования количества степеней свободы критерия Фишера необходимо выполнить следующие шаги:
- Определить количество наблюдений или экспериментов в исследовании. Это может быть количество объектов, событий или условий.
- Определить количество групп или обработок, которым подверглись наблюдения или эксперименты. Каждая группа или обработка должна быть независимой.
- Определить количество степеней свободы для каждой группы или обработки. Для этого необходимо вычислить разницу между общим количеством наблюдений или экспериментов и количеством групп или обработок.
- Вычислить сумму квадратов остатков. Она представляет собой сумму квадратов разниц между наблюдаемыми значениями и предсказанными значениями.
- Вычислить сумму квадратов межгрупповой вариации. Она представляет собой сумму квадратов разниц между средними значениями каждой группы и общим средним значением.
- Используя формулу, вычислить количество степеней свободы критерия Фишера. Количество степеней свободы равно разности между степенями свободы межгрупповой вариации и степенями свободы остатков.
Зная количество степеней свободы критерия Фишера, можно проводить статистический анализ данных, включая проверку гипотез и оценку значимости различий между группами или обработками. Количество степеней свободы помогает определить, насколько статистические различия являются значимыми и позволяет судить о достоверности полученных результатов.
Методика расчета количества степеней свободы критерия Фишера
Степени свободы = n1 - 1, n2 - 1
Где n1 и n2 - количество наблюдений в первой и второй выборках соответственно.
Чтобы использовать эту формулу, необходимо знать объемы выборок, которые сравниваются с помощью критерия Фишера. Обычно данные объемы предварительно известны или могут быть получены из предыдущих исследований или экспериментов.
Пример:
Предположим, что у нас есть две выборки, первая с объемом 20 и вторая с объемом 25. Для вычисления количества степеней свободы критерия Фишера, мы используем формулу:
Степени свободы = 20 - 1, 25 - 1
Степени свободы = 19, 24
В данном случае, количество степеней свободы будет равно 19 и 24 для первой и второй выборок соответственно.
Количество степеней свободы влияет на распределение критерия Фишера и, следовательно, на полученное значение статистики и p-значение, используемые при принятии решения о равенстве или различии дисперсий выборок.
Использование правильного количества степеней свободы является важным аспектом при применении критерия Фишера и позволяет получить достоверные результаты и интерпретацию. Поэтому, при использовании данного критерия, необходимо тщательно провести расчет количества степеней свободы в соответствии с описанной методикой.
Общие принципы определения количества степеней свободы критерия Фишера

Общий принцип определения степеней свободы для критерия Фишера заключается в учете количества групп или общего числа переменных в исследовании.
Если имеется только одна группа или переменная, степени свободы равны 1, так как есть только одна возможность для вариации значений.
Если в исследовании присутствуют две группы или две переменные, то степени свободы будут равны N - 2, где N - общее число наблюдений или выборки. Здесь N уменьшается на 2, так как две группы или две переменные несут информацию и компенсируют друг друга.
Если количество групп или переменных больше двух, то количество степеней свободы зависит от общего количества групп и размера выборки. Общие правила определения числа степеней свободы в этом случае могут быть сложными, и зависят от типа анализа данных. Так как количество переменных влияет на сложность анализа и количество возможных вариаций, различные методы используют различные подходы для определения степеней свободы.
Часто задаваемые вопросы о количестве степеней свободы критерия Фишера
Ниже приведены ответы на некоторые часто задаваемые вопросы о количестве степеней свободы критерия Фишера:
| Вопрос | Ответ |
|---|---|
| Что такое количество степеней свободы критерия Фишера? | Количество степеней свободы критерия Фишера - это показатель, который используется в статистике для определения степени свободы между и внутри групп в случае, когда мы сравниваем дисперсии различных групп. |
| Как вычислить количество степеней свободы критерия Фишера? | Количество степеней свободы критерия Фишера вычисляется на основе количества выборок и размера каждой выборки. Общая формула для вычисления степеней свободы в критерии Фишера имеет вид: DF1 = k - 1 и DF2 = n - k, где k - количество выборок, n - общее количество наблюдений. |
| Зачем нужно знать количество степеней свободы критерия Фишера? | Знание количества степеней свободы критерия Фишера позволяет проводить статистические тесты, например, для проверки гипотез о равенстве дисперсий в различных группах или для оценки влияния факторов на различные области данных. |
| Можете ли вы привести пример использования количества степеней свободы критерия Фишера? | Например, представим, что у нас есть три группы зверей, и мы хотим сравнить их средние веса. Мы можем использовать критерий Фишера для проверки гипотезы о равенстве дисперсий между этими тремя группами. Для этого нам понадобится знание количества степеней свободы критерия Фишера, чтобы правильно интерпретировать результаты теста. |